基于FPGA的网络通讯流量模糊控制器的实现✴

谭会生

(湖南工业大学电气与信息工程学院,湖南株洲 412008)

在数据集成服务和数据包交换网络中,当它们使用多路复用开关网络工作时,不同应用需求的数据包之间是相互影响的.为了针对不同的需求提供不同的服务,采用多优先级控制算法或许是解决不同通讯流量相互影响的一个关键部件.文献[1]提出了一种基于模糊逻辑的多优先级ATM网络控制方法,文献[2]基于模糊逻辑的缓冲管理模式提出了一种高速数据包交换网络的通讯流量高效模糊控制系统,它可应用于像ATM,Internet等数据包交换网络的固定大小和可变大小的数据单元的操作控制.通过对模糊优先权控制模式的性能评估表明,它胜过任一个静态阈值控制器,它的总的吞吐容量非常接近已有参考文献所提出的理想状态的开关控制器的吞吐量.实现模糊控制,传统的方法是使用单片机或DSP实现,但他们存在处理速度受限,程序跑飞等不足,随着EDA技术的发展,若使用FPGA来实现模糊控制,既可提高系统的处理速度,又可增加系统的可靠性[3-8].本文就是基于文献[2]所提出优先模糊控制模型,参考文献[4-6]有关模糊控制器的设计方法,采用并行技术和流水线技术[9],具体研究该系统的FPGA实现问题,重点是FPGA实现结构设计和Verilog HDL程序的设计与验证.

1 模糊控制器的数学模型

网络通讯流量模糊控制器的模型如图1所示,其中输入变量XCLRH,XN和XDN分别表示数据包丢失率,数据包的个数和缓冲器中队列长度变化率,输出变量YACT表示系统对低优先级输入流量采取控制的强度.图2是输入变量XCLRH,XN,XDN和输出变量YACT的隶属函数.其中,变量XCLRH表示高优先级数据包丢失率;XCLRRH为可允许的高优先级数据包丢失率最大值;Q为数据包缓冲器容量的大小.模糊优先控制器的控制规则共30条[2],除规则1,26和30的前件只有两个XCLRH,XN外,其余的规则均包括三个前件,其控制规则的形式如下:ifXCLRHis LOW andXNis Medium andXDNis Negative then theYACTis Strong Admit.

图1 网络通讯流量模糊控制器模型Fig.1 Fuzzy controller model of network traffic managing

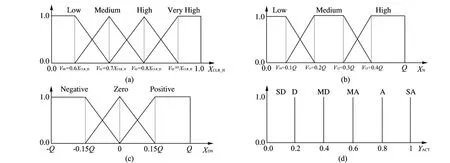
图2 输入变量 XCLR H,XN,XDN和输出变量 YACT的隶属函数Fig.2 Membership functions for the XCLR H,XN,XDNand YACTinput/output variable

该系统可用于分组交换网中对大小固定和大小可变的数据单元的传送控制,比如ATM网络和互联网.该系统可应用于各种实时系统中.

2 模糊控制器的FPGA实现结构

2.1 FPGA实现总体结构

网络通讯流量模糊控制器的FPGA实现结构如图3所示.它由控制规则存储器、模糊化、模糊推理和去模糊化4大部分构成.本系统采用零阶 Takagi-Sugeno模糊推理和去模糊化方法.整个设计基于并行技术和流水线技术.其中系统中模糊化模块、模糊推理模块是串行工作的,而反模糊化模块则和前面二者是并行工作的.

图3 模糊控制器的FPGA实现结构Fig.3 The FPGA implementation architecture of fuzzy logic controller

2.2 模糊化模块的实现

模糊化模块的作用就是先把输入的精确量量化到相应的论域范围,再进行模糊化处理,得到相应的模糊量及隶属度.

1)输入参数的量化.CLR的量化公式如公式(1)所示,其中du=255,XN,XDN的量化公式与此类似,详见参考文献[2].均匀量化后各个输入论域的范围是在0～255之间.

2)输入变量的模糊编码.输入参数量化后,送入比较编码器中进行模糊编码,如图4所示,其中为输入,～为各个模糊区间的中心点(边界点).其工作原理是:先将输入与各边界点进行比较,然后根据比较的结果进行模糊区间编码,并将结果寄存到对应寄存器中.

由隶属度函数的特点可知,对于每个输入变量,最多可以并行输出2个语言值和2个隶属度.根据图2(a)可知,的几个分界点为代入公式(1)量化可得出其分界点分别为26,51,76,128.同理可以求出N和的各分界点.

3)隶属度的计算.设论域为256.因为一个输入变量最多可能属于两个区间,则应分别求对应于每个区间的隶属度大小.其计算模型如图5所示.假如输入X所在区间为(V1,V2),其隶属度为Y,则其它计算类似.

图4 模糊编码原理图Fig.4 Fuzzy encoding principle diagram

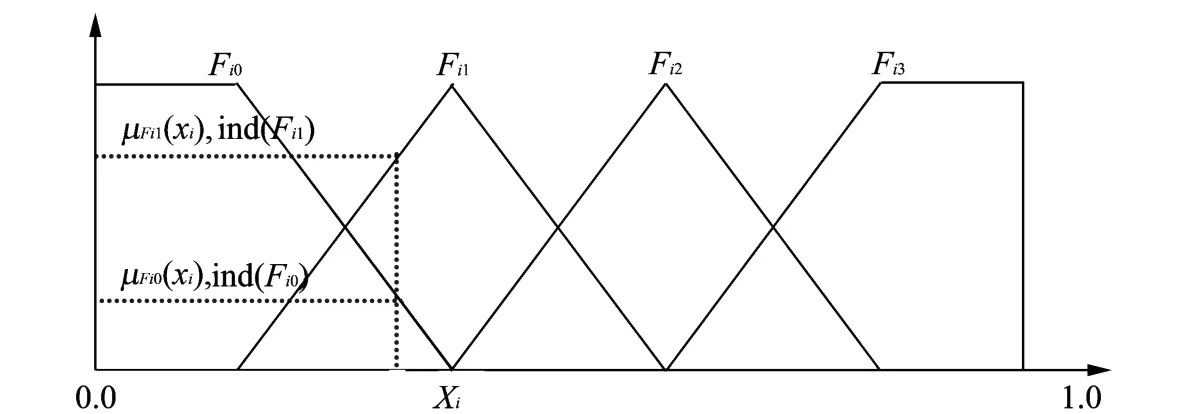
图5 隶属度计算模型Fig.5 Representation of the term set of the input variables

2.3 模糊推理模块的实现

模糊推理主要包括规则的选取和激活度的计算.由本系统隶属函数的特点可知,每个输入变量可并行输出两个语言值和两个隶属度.对三输入系统,最多输出8个语言值和8个隶属度,最多激活8条模糊规则.为降低资源消耗,将对模糊规则进行分组处理,即将三输入系统当作两输入系统处理,因此对于三输入系统,最多输出4组语言值和4组隶属度,而规则表的地址也就可简化为用一个字节来表示.

规则的选取,就是以模糊化模块输出的输入语言值编码作为地址,通过查找相应的隶属度存储器(隶属度存储格式见图3),将其结果送到规则选择器中进行匹配比较,若输入的语言值编码与规则存储器送来的对应前件语言值编码相等,则将其对应的隶属度送入后级的计算激活度模块,否则将0送入计算激活度模块.将输入计算激活度最小值模块的各个隶属度进行比较,求出最小值,即得到前件转移到后件的强度 θi.在求出前件转移到后件的强度的同时,应同时并行地从规则寄存器中读出yi,并暂存在对应的寄存器中.

2.4 去模糊化模块的实现

乘法的硬件实现高效方法有:阵列法,修正布斯算法(MBA法),华莱士树(WT法),修正布斯算法-华莱士树法(MBA-WT)乘法器.A.J.Al-Kbalili和N.Zaman的研究表明,阵列乘法器面积小、功耗小,运算速度慢;WT乘法器和MBA-WT乘法器运算速度快,但功耗较大,WT乘法器面积最大,MBA-WT乘法器面积略大于阵列乘法器;MBA乘法器各项参数介于前三种乘法器之间[10].因此本设计选择修正布斯算法(MBA法),基于MBA的乘法器结构如图6所示.

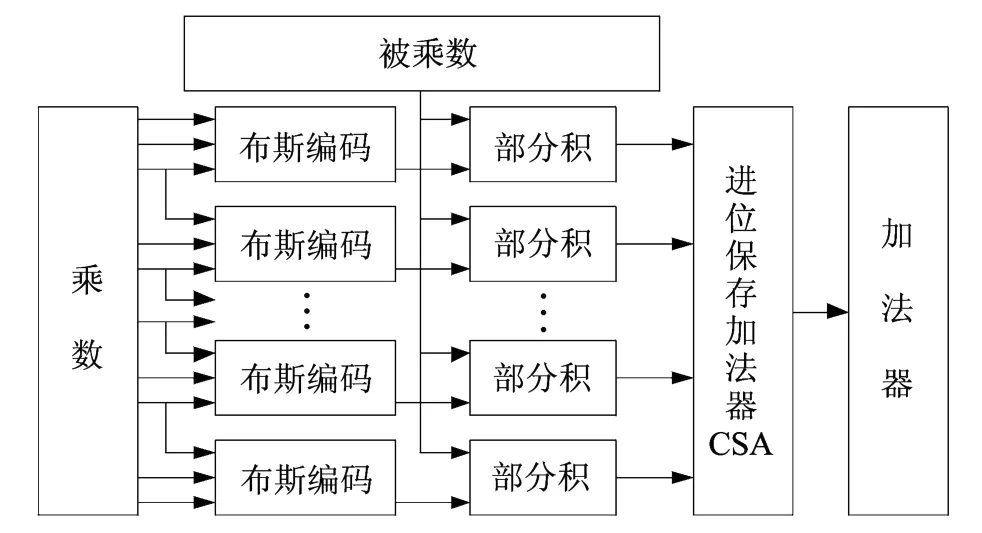
图6 修正布斯算法 MBA乘法器结构图Fig.6 Architecture of modified booth algorithm

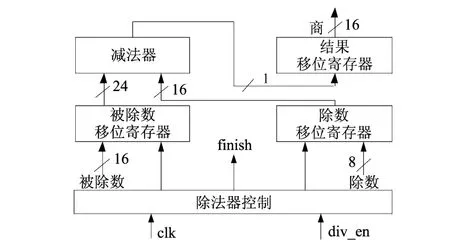
图7 除法器结构图Fig.7 Architecture of divider

本设计的除法器的组成原理结构如图7所示,它是一个16位/8位的除法器,它在16个时钟周期内完成除法运算.与纯组合电路构成的除法器相比,本除法器的最大优点是可以大大节省芯片资源.

2.5 系统控制模块的实现

系统控制模块采用一个米立型状态机来实现.为了减少了高速运转下的状态误码率,提高状态机的稳定性,设计中的状态机采用ONEHOT编码,为使得状态机更加容易维护,其编写方式则采用了三段式状态机的模式.图8为本系统控制模块的状态图.

图8 系统控制模块的状态图Fig.8 State diagram of system control module

3 控制器的FPGA实现结果

本系统采用Verilog硬件描述语言进行逻辑描述,采用Quartus 8.0和Modelsim SE 6.0进行作为设计和调试的工具,最后选用Altera公司的Stratix II系列中的EP2S15F484C3芯片实现了本系统.其主要模块及系统总体的仿真结果分别如图9～图12所示.经分析,系统的逻辑功能符合系统的设计要求,证明了Verilog程序的正确.逻辑综合适配后,系统消耗的资源为:Total AlUTs 548/12 480(4%),Totals registers 203,Total memory bits 20032/419 328(5%),Total PLLs 1/6(17%);系统的最高时钟频率是273.22 MHz.

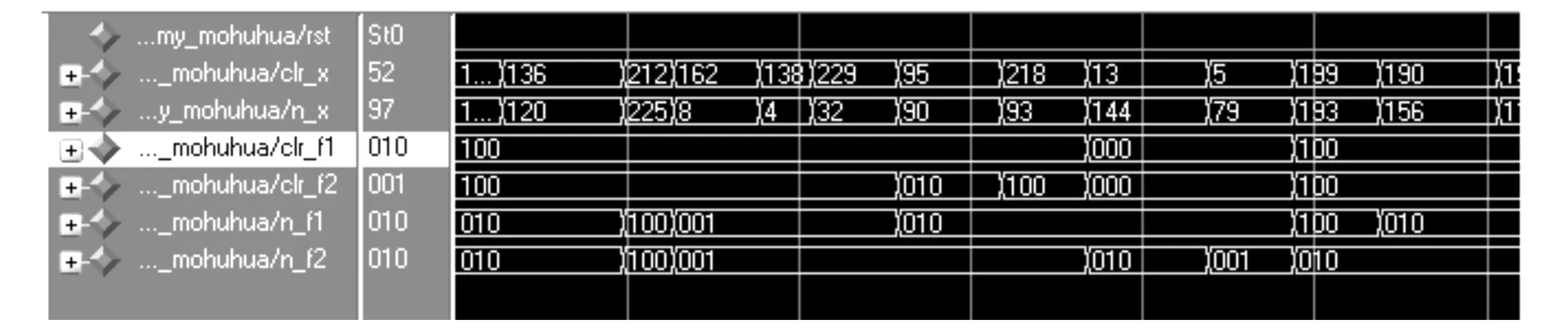
图9 模糊化模块的功能仿真结果Fig.9 Functional simulation result of fuzzification module

图10 模糊推理模块的功能仿真结果Fig.10 Functional simulation result of fuzzy inference module

图11 去模糊模块的功能仿真结果Fig.11 Functional simulation result of defuzzification module

图12 模糊控制器的功能仿真结果Fig.12 Functional simulation result of fuzzy controller

4 结 论

基于FPGA开发了一个用于网络通信流量的模糊控制器.该模糊控制器是利用缓冲器和模糊控制技术对不同优先级的通信流量进行管理,既可保证高优先级通讯的服务质量,又可利用未使用的缓冲资源去提供最有效的通信控制,以增大系统的吞吐容量.基于优先模糊控制原理和并行技术、流水线技术等硬件设计优化技术,提出了基于FPGA的网络流量优先模糊控制器的总体实现结构和模糊化、模糊推理和去模糊化模块的实现方法,给出了Verilog HDL程序实现的功能仿真、逻辑综合及典型时序分析结果.实验结果验证了本控制器结构设计的有效性和程序设计的正确性,并且与传统的单片机或DSP实现方法相比,既提高了系统的实时性,又增加了系统的可靠性,而且系统非常容易修改和移植.本系统可以应用于ATM和IP网络的流量控制,修改后也可应用于智能交通控制.

[1]Catania V,Ficili G,Panno D.A fuzzy logic based approach to multipriority control in ATM networks[J].Computer Standards&Interfaces,1999(21):19-23.

[2]Ascia G,Gatania V,Panno D.An efficient fuzzy system for traffic management in high-speed packet-switched networks[J].Soft Computing,2001(5):247-256.

[3]Tessier R,Burleson W.Reconfigurable computing for digital signal processing:a survey[J].Journal of VLSI Signal Processing,2001(28):151-163.

[4]Monmasson E,Cirstea M N.FPGA design methodology for industrial control systems—a review[J].IEEE Transctions on Industrial Electronics,2007,54(4):1824-1842.

[5]Guo Yongqiang,Fang Kangling.Design of Fuzzy Feed-forward Decoupling System based on FPGA[C].The 2008 International Conference on Embedded Software and Systems(ICESS2008),IEEE computer society,2008:405-409.

[6]Juang Chiafeng,Lu Chunming,Lo Chiang,et al.Ant colony optimization algorithm for fuzzy controller cesign and its FPGA implementation[J].IEEE Transactions of Industrial Electronics,2008,55(3):1453-1462.

[7]Evmorfopoulos N E,Avaritsiotis J N.An adaptive digital fuzzy architecture for application-specific integrated circuits[J].Active and Passive Elec.Comp.,2002(25):289-306.

[8]白瑞林,江吕锋,王建.基于FPGA的模糊自整定PID控制器的研究[J].仪器仪表学报,2005,26(8):833-837.

Bai Ruilin,Jiang Lvfeng,Wang Jian.The study of fuzzy self-tuning PID controller based on FPGA[J].Chinese Journal of Scientific Instrument,2005,26(8):833-837.(in Chinese)

[9]Shanbhag N R.Algorithms transformation techniques for low-power wireless VLSI systems design[J].International Journal of Wireless Information Networks,1998,5(2):147-170.

[10]Al-Khalili A J.32-bit constant(k)coefficient multiplier[J].IEEE Catalogue CH37239,2001(1):306-308.