基于有限元仿真的简支梁结构损伤分析✴

罗 裴

(武汉理工大学光纤传感技术国家工程实验室,湖北武汉 430070)

结构的损伤源于微小裂纹,而裂纹的产生将影响结构的振动特性参数.通过分析结构的振动特性参数即可预测和确定损伤的产生和位置[1-2].在研究结构损伤识别之前,需要对结构进行理论计算和模拟,这样可减少实际工作量,同时还可少走弯路.因此,对结构的理论计算和模拟在结构损伤检测中起着极为重要的作用,也为准确识别损伤奠定基础.

有限元分析软件是结构分析中的通用软件,以有限元分析结果作为结构损伤识别的参考,对结构损伤识别的实现具有指导性作用[3-7],因此,采用有限元分析软件对结构进行实验前的理论计算和模拟,将对实验结果起着指导性的作用.

本文采用有限元分析软件,对待研究简支梁结构进行了前期的计算和分析,模拟了简支梁结构在未损伤、单个损伤、多个损伤的模态频率和振型的变化,并对模拟的结果进行了比较和分析.

1 简支梁的振动特性分析

要研究裂纹对简支梁振动特性的影响,必须先建立完好梁和裂纹梁的振动力学模型,然后对比研究不同状况下的梁的振动特性,从而探讨裂纹对梁振动的影响规律[1].

根据结构动力学理论,结构自由振动的方程可以表示为

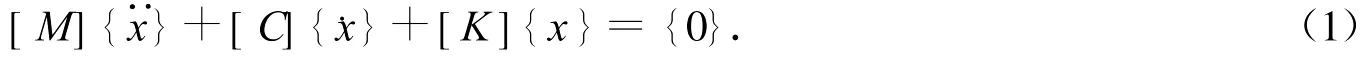
其特征方程可以表示为

由式(2)可以看出,结构的固有频率主要与结构的刚度和质量有关,因此,当结构发生损伤时,结构的刚度和质量均会发生变化.而二者的变化必然会引起结构的固有频率和振型发生变化,那么,由式(2),可以得出结构发生损伤后的特征方程

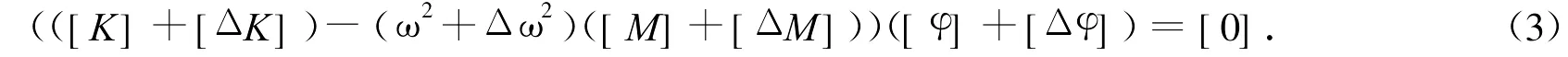
在实际发生损伤的裂纹结构中,结构质量发生改变非常小,可以忽略不计,因此,在忽略质量改变的情况下,式(3)可写为

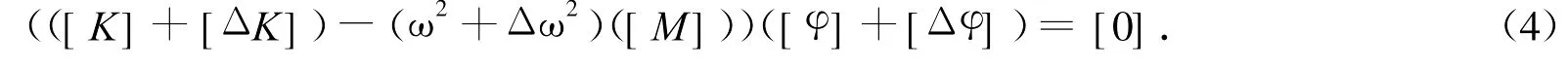
把式(4)展开,并忽略频率的平方项,则得固有频率的改变量为

对于第i阶振型[φi]有

式(6)即为频率损伤方程.若结构发生损伤后,第j个单元刚度发生的变化为[ΔKj],则式(6)可变为

若假设特征值的变化可以表示为单元损伤位置和损伤程度的函数,即

βj为一个标量,它表示第j个单元的损伤程度,有下式成立

将式(9)代入式(7),可得

由式(10)可知,简支梁结构的频率变化不仅依赖于结构的损伤位置,而且依赖于损伤程度.因此,通过简支梁的自由振动方程,可求出简支梁的各阶固有频率,而且不同的裂纹长度对梁的刚度的影响不同.随着单元刚度的减小,简支梁各阶自振频率逐渐减少;对称位置的单元刚度降低幅度相同时,对频率的影响也相同,由于不同位置的损伤程度有区别,也会引起相同频率的变化值.当单元刚度降低较小时,裂纹简支梁各阶自振频率变化不大,当简支梁损伤单元的刚度降低超过50%或者更大时,简支梁的自振频率减少量就会明显增大.

2 简支梁结构有限元模型的建立

在实验装置搭建之前,进行有限元分析是十分必要的.通过在有限元分析软件上对研究结构进行结构参数的模拟,从而确定待研究结构的基本尺寸和材料.在确定这些基本参数后,将对损伤结构的模态参数进行模拟,并获得有效数据.

根据有限元分析的模拟和计算,确定待模拟的简支梁的基本参数为:长 1.5 m,宽 0.1 m,高0.005 m,弹性模量为210 GPa,泊松比为0.3,密度为(7.8)3.所得到的简支梁完好与有损伤的有限元模型分别如图1,图2所示,其中,图2对模型进行了放大,可以清晰地看见损伤的位置.网格的大小为0.005 m,裂纹宽度为0.001 m.

图1 未损伤简支梁有限元模型Fig.1 Finite element model of simple-supported beam with no damage

图2 一个损伤简支梁有限元模型Fig.2 Finite element model of simple-supported with one damage

在用ANSYS10进行模拟计算过程中,由于所采用的简支梁比较薄,故简支梁单元采用SHELL63,所得简支梁在不同损伤状况下的各阶固有频率模拟结果如表1,表2所示.

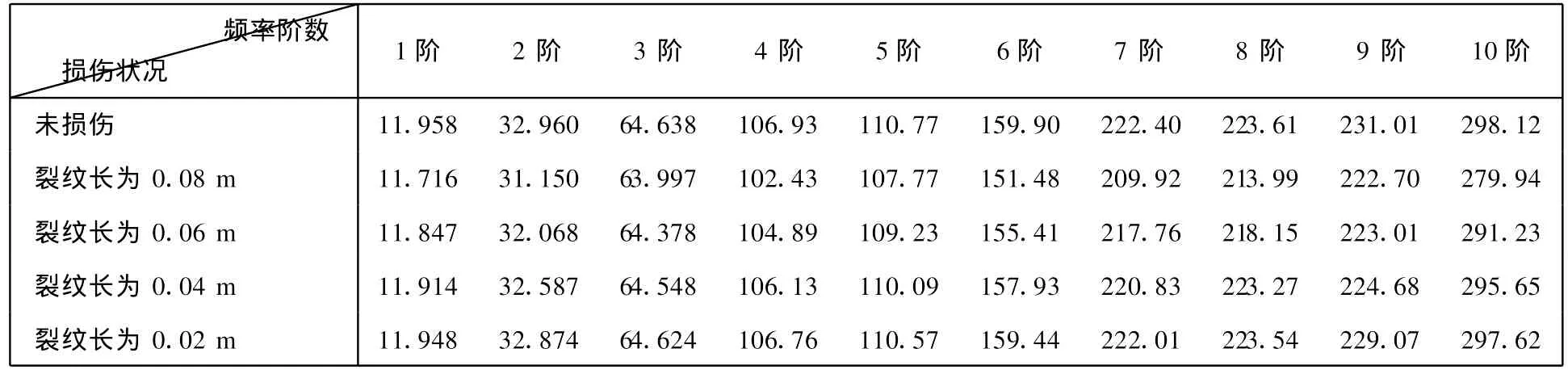
表1 简支梁在完好和损伤在同一位置但损伤程度不同的情况下的各阶频率的变化Tab.1 Changes of each order frequency of simple-supported beam under different damage status of the same location with no damage and damages

表2 简支梁在不同损伤个数状况下的各阶频率的变化情况Tab.2 Changes of each order frequencies of simple-supported beam under different damage status

由表2可以看出,损伤越严重,简支梁的各阶频率变化就越大,在低频阶段,频率变化随损伤程度的变化不大,在高频阶段,简支梁的各阶频率的变化较明显.

表1研究了未损伤和在同一位置损伤的不同程度的简支梁各阶固有频率变化状况,表2研究了简支梁在一个损伤、两个损伤和三个损伤以及一个损伤在不同位置状况下固有频率的变化.由表 2可以看出,损伤个数越多,梁的固有频率的变化就越大,但也有个别频率因多个损伤位置的不同而出现不同的变化,但总体来说,有损伤,则固有频率必有变化;而损伤位置不同,对各阶频率的影响也不同,由表2可以看出,当损伤在0.3 m处时,其4,5,6,10阶固有频率的变化比当损伤在0.8 m处时的相应阶固有频率的变化要大,而其他阶的固有频率的变化则相反,因此,可以看出,损伤位置的不同,其对各阶固有频率的影响不同.因此,在研究简支梁结构的损伤识别时,若采用固有频率进行损伤识别,必须针对同一位置而言,否则将得出错误结果.同时也说明,损伤识别前的模拟计算十分重要.

3 简支梁结构振型的有限元分析

前面研究了简支梁结构在不同损伤状况下的固有频率的变化,下面将研究简支梁在不同损伤状况下的振型的变化,同样采用有限元分析软件进行模拟和计算,主要研究简支梁在完好和一个损伤、三个损伤状况下的振型的变化,并进行比较,从中寻找简支梁的振型在不同损伤状况下的变化规律.图 3～9是简支梁在未损伤,一个损伤,三个损伤状况下的振型比较图.

从简支梁在不同损伤状况下的振型图可以看出,当简支梁结构有损伤时,其振型就有明显的变化.在振型图中可以看到,结构一旦发生损伤,其振型图均有变化,结构的损伤个数越多,其振型图变化就越明显(见图 11),因此,若采用振型来进行结构损伤识别也是完全可以实现的,而且精度比较高,这在很多文献中均有报道.

图3 未损伤简支梁的 1阶振型Fig.3 One order vibration mode of simple-supported beam with no damage

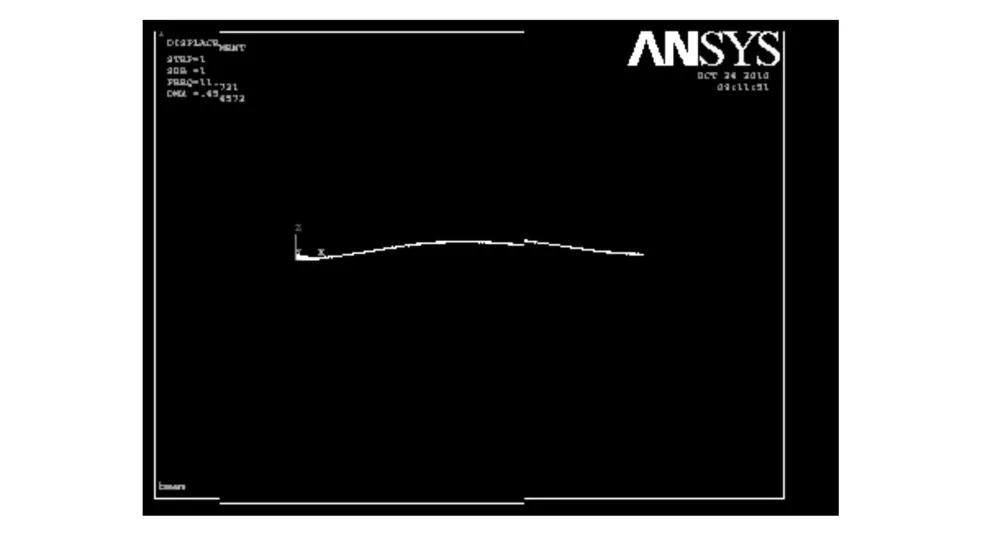
图4 一个损伤简支梁的1阶振型Fig.4 One order vibration mode of simple-supported beam with one damage

图5 三个损伤简支梁的1阶振型Fig.5 One order vibration mode of simple-supported beam with three damages［HT］

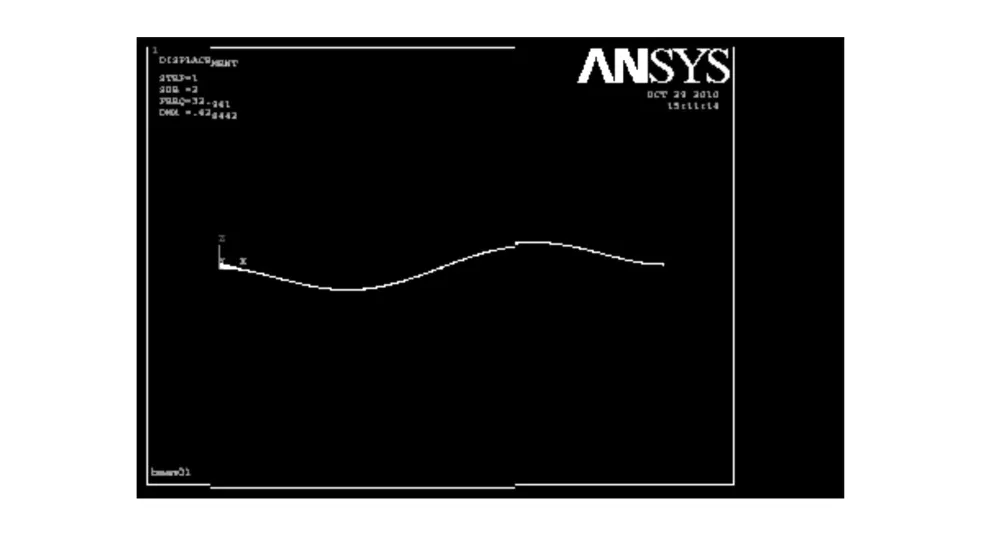
图6 完好简支梁的2阶振型Fig.6 Two order vibration mode of simple-supported beam with no damage

图7 一个损伤简支梁的 2阶振型Fig.7 Two order vibration mode of simple-supported beam with one damages

图8 三个损伤简支梁的2阶振型Fig.8 Two order vibration mode of simple-supported beam with three damages

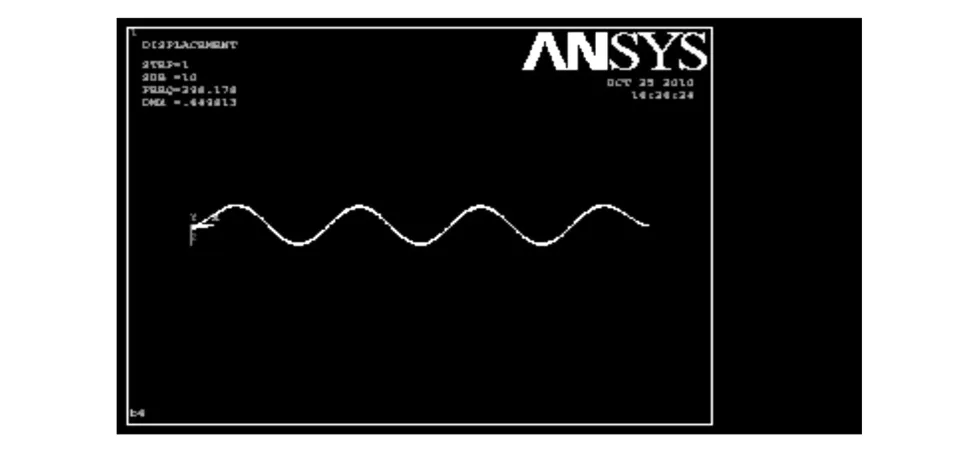
图9 未损伤简支梁的 10阶振型Fig.9 Ten order vibration mode of simple-supported beam with no damage

图10 一个损伤简支梁的10阶振型Fig.10 Ten order vibration mode of simple-supported beam with one damage

图11 三个损伤简支梁的 10阶振型Fig.11 Tenth-order vibration mode of simple-supported beam with three damages

4 结 论

由有限元分析方法模拟计算发现,损伤裂纹使简支梁结构各阶固有频率降低,且各阶固有频率的下降幅度随裂纹的相对深度增大而增大;简支梁结构的各阶固有频率和振型随损伤裂纹深度增大呈现规律性变化,裂纹深度对梁固有频率的影响与裂纹位置密切相关,但不同位置的裂纹对同阶和不同阶的固有频率的影响并不相同.

[1]李学平,余志武.含多处裂纹梁的振动分析[J].应用力学学报,2007,24(1):66-69.

Li Xueping,Yu Zhiwu.Vibration analysis to multiple cracked beam[J].Chinese Journal of Applied Mechanics,2007,24(1):66-69.(in Chinese)

[2]Moaveni P H S.Finite element analysis-theory and application with ANSYS[J].Minerals Engineering,1999,12(8):992-993.

[3]高丽宏,龙江启.基于有限元模型的梁结构损伤识别技术研究[J].茂名学院学报,2006,16(3):70-74.

Gao Lihong,Long Jiangqi.A Study of the damage identification techniques for beam structures based on finite element method[J].Journal of MaoMing College,2006,16(3):70-74.(in Chinese)

[4]武喜.基于有限元的简支梁加固受力分析的研究[J].科学之友,2010(7):66-68.

Wu Xi.Simply supported beams reinforcement stress analysis with finite element[J].Friend of Science Amateurs,2010(7):66-68.(in Chinese)

[5]李建,薛刚,李奉阁.损伤简支梁模态频率变化规律有限元分析[J].内蒙古科技大学学报,2009,28(4):350-353.

Li Jian,Xue Gang,Li Fengge.Finite element analysis on modal frequency change regulations of the damage simple-supported beams[J].Journal of Inner Mongolia University Science and Technology,2009,28(4):350-353.(in Chinese)

[6]Damatty A A E,Rahman M,Ragheb O.Component testing and finite element modeling of standing seam roofs[J].Thin-Walled Structures,2003,41(11):1053-1072.

[7]Her S C,Liang Y C.The finite element analysis of composite laminates and shell structures subjected to low velocity impact[J].Composite Structures,2004,66(4):277-285.