密封环扰动状态下稳定性分析及动态响应

宫 燃，葛如海，谢明祥

(1.江苏大学 汽车与交通工程学院，镇江 212013;2.浙江大学 机械工程学系，杭州 310027)

涨圈型密封环是属于流体动密封的一类部件。在工程应用类重载车辆中，传动装置中湿式离合器使用涨圈型密封环作为流体密封装置来实现其结合油压的建立。密封性能影响到传动装置的动力性和稳定性，是评价总体传动性能的一个重要指标。

随着使用条件的提高，特别是要满足车辆大功率的传动需求，密封环需要在高速、高压、高温工况下运行。在实际使用中，密封环却出现了提早失效的现象，直接影响到整个传动装置的使用性能，其失效形式是密封环的密封面磨损，引起密封实际接触面积减小，泄漏量增多等失效现象，影响传动系统的正常运行。引起密封环磨损的原因有很多，而非正常磨损是导致密封性能恶劣以及加速失效的显著因素［1，2］，其中最不应忽视的就是密封环在轴向或角向扰动下的偏摆而导致局部碰摩产生磨损问题。

在实际工况中，受车辆工况波动、冲击和传动系统零部件加工精度的影响，密封环工作状态下受到随机扰动而产生偏摆，这将改变密封端面间的油膜厚度，并导致承载力、泄漏量和摩擦扭矩等密封特性参数的变化［3，4］，引起密封面产生局部不均匀磨损。现有关于密封环的研究成果多基于过程稳态的假设［5，6］，无法真实考察密封环在扰动下的状态响应。因此在密封环的设计和试验阶段，掌握非稳定因素对密封面磨损的影响，研究在扰动状态下密封环的稳定性及其动态响应情况，以期为设计和开发适用于高功率密度传动的旋转密封件提供科学依据。本文重点讨论在扰动状态下密封环的稳定性，以及动态响应导致磨损的情况。

1 扰动模型

涨圈型密封环通常在一定的介质温度、介质压力和旋转速度下稳定运转，是密封环正常工作的前提［7］。在这样的负荷下，密封环与旋转轴凹槽侧面组成一对摩擦副，正常工作时相互贴合且相对转动并实现密封，图1表示密封环纵向截面结构和密封原理。

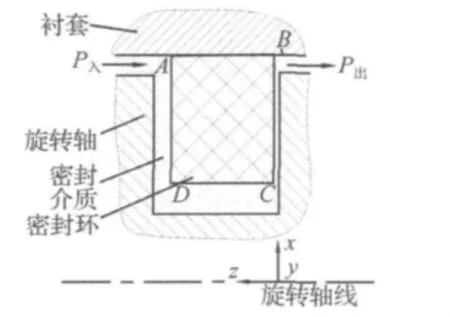
图1 密封环结构和原理示意图Fig.1 Schematic diagram of rotary seal

分析扰动状态下动态响应及其对密封面磨损的影响，需要得到密封环的运动方程和扰动作用下密封环的润滑方程，在此基础上分析稳定性，从而指定各个因素对密封环稳定性及其磨损的影响规律。

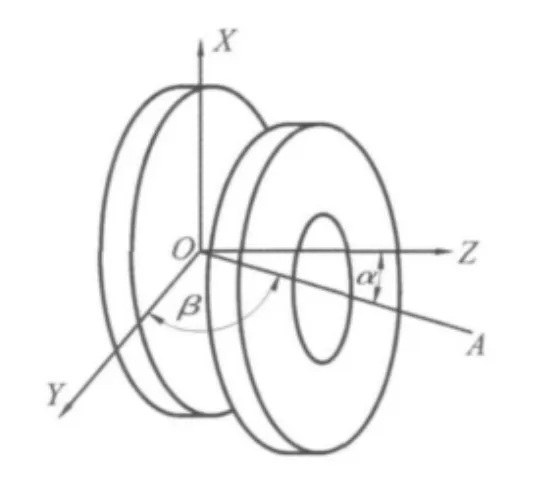
图2 扰动分析模型及坐标系Fig.2 Seal ring under perturbation and coordinate system

密封环扰动分析模型及坐标系如图2所示。坐标原点建立在旋转轴横截面的圆心位置上，密封环既可轴向移动又可角向摆动，OA表示密封环空间偏移的圆心位置与坐标原点的连线。密封环的扰动有三个自由度，即沿Z轴的轴向移动z、绕X轴的角向摆动α和绕Y轴的角向摆动β，相应的扰动位移和扰动速度分别用z，α，β和来表示。

按照图2的模型，得到密封环在微扰下的运动方程，表示为:

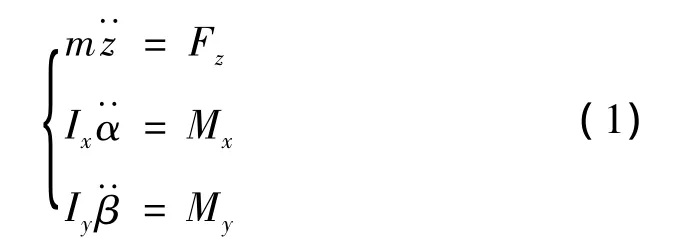
式中:m为密封环质量，kg;Fz、Mx、My分别为密封环的轴向作用力，N，及 X 向、Y 向动态力矩，N/m2;Ix，Iy为分别为密封环绕X和Y轴的转动惯量，kg·m2。由于密封环的轴对称性，有Ix=Iy=I。

微扰位移和微扰速度使油膜厚度变化，影响油膜压力，进而影响油膜对密封环的作用力和力矩，即Fz、Mx、My也是微扰位移和微扰速度的函数［8］，则运用Taylor展开，保留到微扰为一次方的线性项，得到式(2)～式(4):

式中:Fz0、Mx0、My0为在平衡位置时油膜对密封环的力与力矩;Fz'、Mx'、My'为微扰产生的作用力与力矩的增量。

轴向微扰和角向微扰之间的交叉作用较微小故忽略不计［9］。这样根据式(2)～式(4)，可以定义轴向、周向的刚度系数和阻尼系数，表示如下:

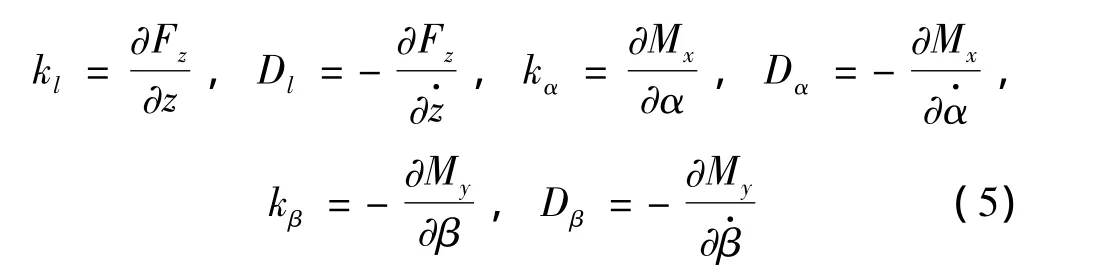
式(2)～式(4)中微扰产生的作用力Fz'及偏转力矩Mx'，My'是由于油膜的微扰压力 p'引起的，有下式成立:

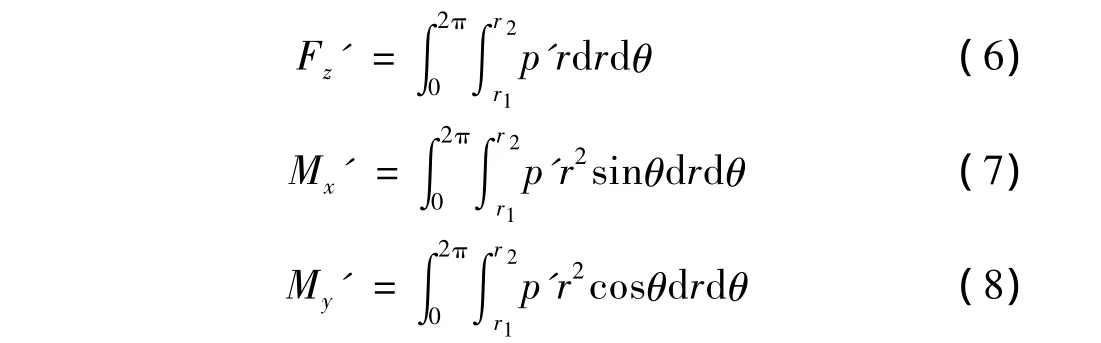
式中:r1、r2为分别为密封环的内径和外径，mm。

其中微扰压力p'应视作密封环的微扰位移和微扰速度的函数，利用Taylor展开，并只保留线性项，得到:

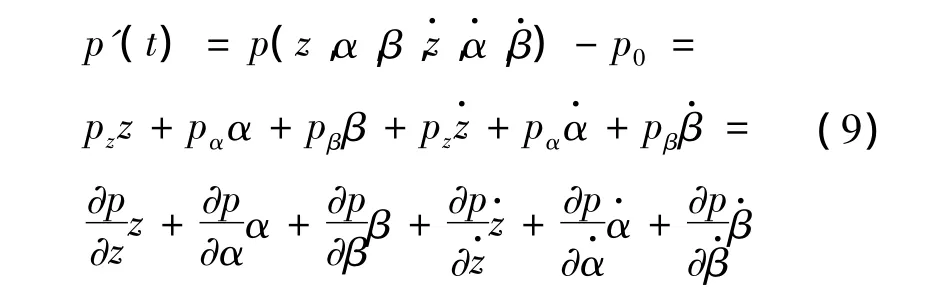
式中:p0为油膜的稳态压力，即平衡位置时油膜的压力，MPa;p为油膜的瞬态压力，MPa;pz、pα、pβ为分别对应扰动位移和扰动速度的微扰压力，MPa。

这样根据式(5)的定义，把式(6)～式(9)代入其中，得到:

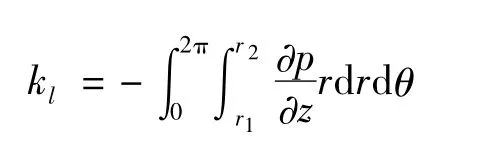
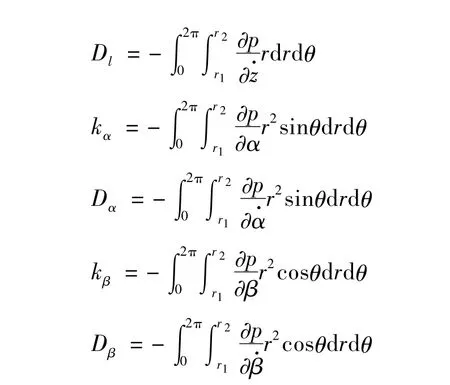
图3表示密封环动态特性系数计算的分析模型与坐标系，坐标系X轴建立在密封环的动平衡位置上，efgh代表密封环的横向截面，在扰动的影响下，密封面位于e'f'g'h'位置。密封环的独立扰动有三个自由度，如图3所示，β为密封环绕Y轴的偏摆角，α为密封环绕X轴的偏摆在YZ平面上的投影角，z表示密封环在Z轴方向的移动距离。

根据图2和图3，在扰动时油膜厚度会发生变化，表示为:

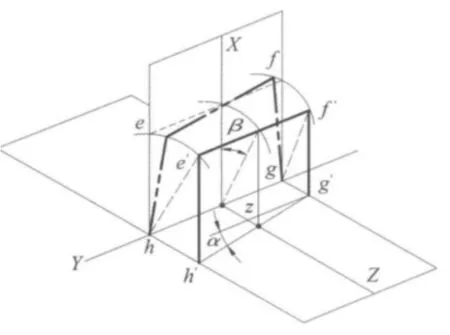
图3 密封环动态参数计算模型Fig.3 Compution model of dynamic coefficients

式中:h0为油膜的稳态厚度，mm。

其中θ为密封环圆周角，其起始线与Y轴重合。

2 润滑方程

如果获得密封环扰动下的规律，需要计算油膜对密封环的作用力Fz及偏转力矩Mx、My。这样需要建立和求解Reynolds方程，通过油膜压力求得力和力矩值。在此需要考虑膜厚变化的影响，因为在扰动影响下密封环偏摆使油膜厚度不断变化，引起油膜压力产生变化，这样写出在密封环扰动时的Reynolds方程:

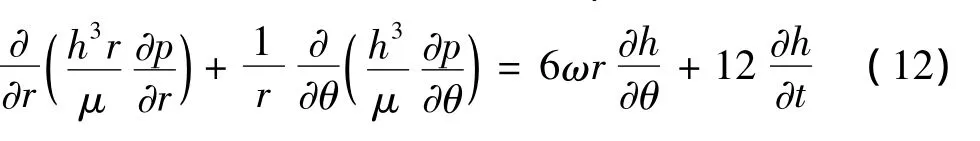
由于在Reynolds方程中考虑了油膜的变厚度，方程中的系数不是常数，故整个方程呈现出非线性特征。在本文中采用有限差分法来求解Reynolds方程，在求解域内采用中间差分格式进行离散。单元的中间差分格式表示为［10］:

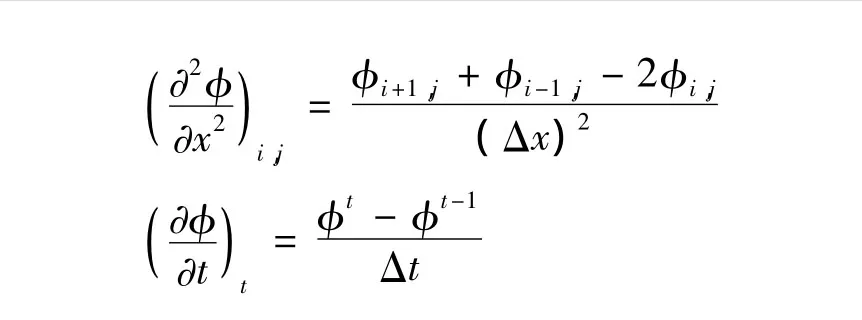
式中的φ代表文中所求的未知量，例如膜厚h，压力p等，φt表示在t时刻的取值，i与j代表离散后的节点，Δt表示时间间隔。

将求解域离散划分成多个单元后，离散方程应用到求解域中每个待求节点上，最终可得到一非线性方程组。对方程采用无量纲形式，定义无量纲的刚度与阻尼系数:

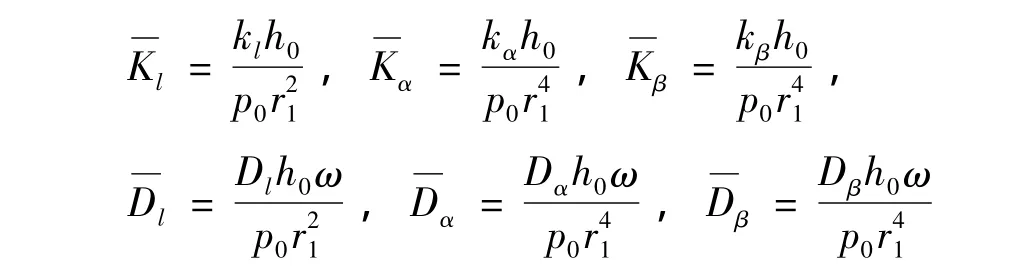
在某一油膜厚度下迭代求解各节点油膜压力时，利用下式来判断迭代计算是否达敛:

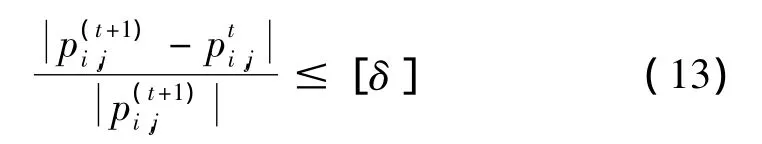
其中pi，j为求解域内任意一节点油膜压力;t表示时间量;［δ］为一给定收敛误差，以此来控制油膜压力的收敛精度，取0.001。如果计算所得油膜压力不满足式(13)，则需重新进行迭代计算。

3 结果分析

以外径为125 mm的密封环作为研究对象，模型几何参数为:内径119.2 mm，轴向厚度2.6 mm，密封介质为15W－40CD柴油机油。建立密封环模型，对模型进行离散，得到密封环差分网格模型，模型共1580个单元。数值计算得到几组反映参数对偏摆的影响规律曲线，如图4所示。设定初始条件后，给密封环一个初始绕X轴偏转的扰动，使它开始运动，求解方程，得到在压力1.8 MPa，转速3500 r/min的给定工况下密封环的受扰响应，如图4(a)，表示X向偏转角度与偏转力矩的关系曲线。随着偏转角度的增大，由此而引起的油膜对密封环的偏转力矩也随之增加，但偏转到达一定程度时，偏转力矩增长缓慢，最后保持平稳。在偏转力矩的作用下，密封环发生倾斜，导致密封面的局部磨损。引起密封环偏转的因素主要有:端面压力的不轴对称分布、密封环外圆柱面的不均匀磨损，主轴的端面跳动及加工精度的影响等。引起油膜压力分布不均的原因有密封环密封面本身的不平度，同时在磨损过程中端面的不均匀磨损等，都将引起端面压力的不对称，引起密封环偏转或倾斜。如果密封环随轴转动，由于各部分磨损程度的不同，会在油压作用下发生扭转，产生偏转力矩。另外，主轴的端面跳动、进油衬套内径较大的椭圆度等这些装配和加工质量问题也在干扰密封环的平衡状态，偏离平衡位置导致局部接触产生磨损。

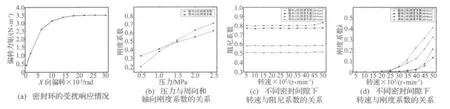
图4 偏摆及动态特性的影响规律曲线Fig.4 Law curves of run-out and dynamic coefficients

从图4(b)可知，在密封间隙不变的情况下，无量纲轴向刚度系数与周向刚度系数随着油压的增加而增大，轴向刚度系数的上升幅度更大一些，说明压力越大，产生轴向作用的动态力更加明显，磨损的机率也会更大。图4(c)与图4(d)是转速与阻尼系数、刚度系数的关系曲线。由图4(c)可知，无论是轴向阻尼系数还是周向阻尼系数基本不随转速变化，曲线基本呈现平行趋势，只是在高转速下，大于4500 r/min时曲线有轻微的上扬，以膜厚为8μm时的周向阻尼系数变化最为明显，说明在高速大膜厚时可以减缓周向的偏摆，但影响有限。另一方面，密封端面间隙即油膜厚度的变化对阻尼系数有影响，间隙越大阻尼系数越大。油膜厚度增加一倍时，阻尼系数值也近50%的幅度增加，表明膜厚是衰减扰动的一个显著因素。图4(d)表示不同密封间隙下转速与刚度系数关系。在转速低于2500 r/min时，刚度系数基本为零，说明在较低转速下，产生扰动的作用并不明显。在转速大于3500 r/min时刚度系数才逐渐增大，随着速度的进一步增加，刚度系数的增长趋势明显，高转速下的刚度大于低转速下的刚度，表明转速是影响刚度系数的重要因素，也是触发扰动的条件之一。由图进一步得出，密封间隙的影响也更加明显，在密封间隙由4μm增大到8μm时，刚度系数显著减小，说明在膜厚较大时，密封的不稳定性增强，使密封工作在小间隙下，从而具有较高的刚度，更有利于密封环的稳定。

4 结论

本文考察了重载车辆传动装置密封环在扰动状态下油膜厚度的变化规律，建立扰动运动模型，联立扰动状态下的时变Reynolds方程，经过数值计算得到偏摆对密封稳定性和密封面磨损的影响规律和特征。

由分析结果可知，降低偏摆的影响需要提高密封环及其装配件的加工精度，同时也要降低密封环的初始变形及累积的密封环局部磨损的影响，因为往往这样的变形或磨损会引起压力分布不均。经过分析表明油膜厚度对扰动有较强的干预作用，恰当的控制膜厚是一举两得的方法:不但可以减小端面磨损，还可以降低扰动的影响。基于这点，对密封环的设计可以考虑采用密封环结构型式优化来达到这样的效果。

［1］Green I.A transient dynamic analysis of mechanical seals including asperity contact and face deformation［J］.Tribology Transactions，2002，45(3):284 －293.

［2］Salant R F，Cao B.Unsteady analysis of a mechanical seal using Duhamel’s method［J］.Journal of Tribology，2005，127(3):623－631.

［3］Kaneko S，Tanaka T，Abe S，et al.A study on squeeze films between porous rubber surface and rigid surface:analysis based on the viscoelastic continuum model［J］.Journal of Tribology，2004，126(7):19 －27.

［4］朱汉华，严新平，刘正林，等.转速对油膜刚度与螺旋桨轴振动影响［J］.船海工程，2007，36(4):83－85.

［5］周 丹，盛选禹.水平孔道O形环密封结构有限元接触分析［J］.核动力工程，2008，29(5):22－24.

［6］Sekiguchi S，Suzuki H，Ryper R G，et al.Development of a new seal material to reduce energy losses in vehicle transmissions［J］.Sealing Technology，2009(11):8 － 11.

［7］顾永泉.流体动密封［M］.北京:中国石化出版社，1990.

［8］徐 华，朱 均.螺旋槽式液体机械密封的动力学性能分析［J］.西安交通大学学报，2004，38(5):474 －478.

［9］刘雨川，徐万孚，王之栎，等.端面气膜密封动力特性系数的计算［J］.清华大学学报(自然科学版)，2002，42(2):185－189.

［10］阎 超.计算流体力学方法及应用［M］.北京:北京航空航天大学出版社，2006.