汽车减振器外特性仿真与试验分析

徐中明，李仕生，张志飞，杨建国，李传兵

(1.重庆大学 机械工程学院，重庆 400030;2.重庆大学 汽车噪声振动和安全技术国家重点实验室，重庆 400030)

减振器是汽车的重要组成部分，其动态阻尼特性对于整车动力学性能具有很大的影响［1，2］。但传统设计方法主要根据经验确定设计参数然后进行试验修正，需要进行反复调整，并经多次试制与试验，这种设计方法不但周期长、成本高，而且较难获得最优的减振器特性。基于此，从20世纪70年代开始，国外学者就开展了传统液压减振器工作特性的建模分析研究。如Duym［3］建立了减振器各腔室间流动的模型，对减振器速度特性的滞后现象进行了专门的研究，另外他在还建立了考虑温度影响的参数模型。但这些文献建立的模型大多是利用实验测试结果来获得部分或全部模型参数，因此不便于在设计阶段预测减振器特性。Lee等［4］建立了一种既能展示减振器特性又较为简明的模型;Besinger等［5］建立了重型车辆悬架减振器的模型。但作为试探性的工作，这些模型仿真结果仅在减振器的低频运动工况下能够与实验结果较好地吻合。

目前，国内对一般双筒液压减振器的建模过程中应用了流体力学缝隙流动、管嘴流动、薄壁小孔节流理论［6］。但大多仅考虑了复原阀、压缩阀的工况，而忽略了流通阀及补偿阀的影响;同时对于阀系采用纯阀片结构的减振器，工作过程中其阀片属于“受均布载荷作用的环形薄板阀片挠曲变形”，而采用此方法建立减振器数学模型的文献却很少。因此本文采用“受均布载荷作用的环形薄板阀片挠曲变形”方法建立数学模型，在建模过程中考虑补偿阀及流通阀对阻尼力的影响，同时对比分析了在建模中考虑与不考虑“补偿阀”及“流通阀”二种情况对仿真后的减振器阻尼力的结果影响规律，分析了“补偿阀”及“流通阀”阀系结构参数变化时对减振器阻尼力的影响及敏感程度。

1 阀片弯曲变形微分方程

如图1所示是减振器阀系采用纯阀片结构时圆环形弹性阀片的装配示意图。阀片内圆是固定约束，其约束的内半径为ra，外圆是自由约束，外半径为rb，阀片厚度为δ，所受压力为 p，在半径r处弯曲变形量为fr。

以节流阀片圆心为极点建立极坐标系，由于结构和载荷都是绕中心轴对称，根据弹性力学原理可得薄板弹性阀片弯曲变形曲面微分方程［7－9］

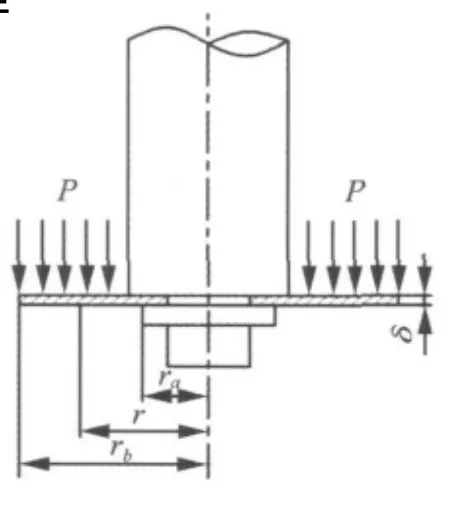
图1 阀片力学模型Fig.1 Mechanical model of throttle-slice

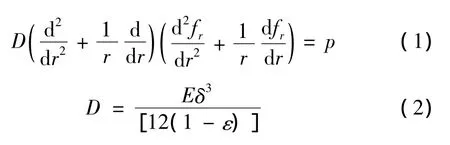
式中:E为阀片弹性模量，ε为泊松比;r为极径，r∈［ra，rb］。

当多个阀片叠加时，δ需按等效厚度计算［9，10］，即:

因此，微分方程(1)的通解表达式为:

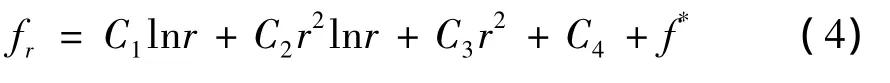
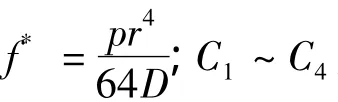
求解 C1，C2，C3，C4后的结果为［8］:

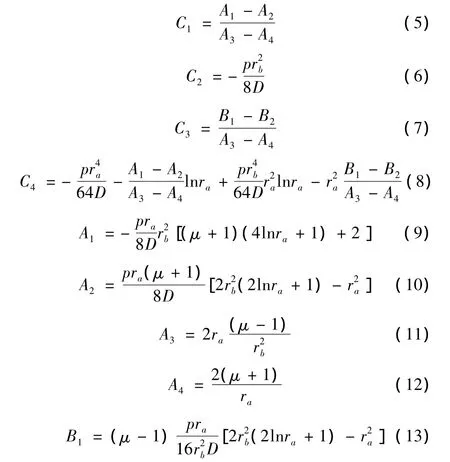
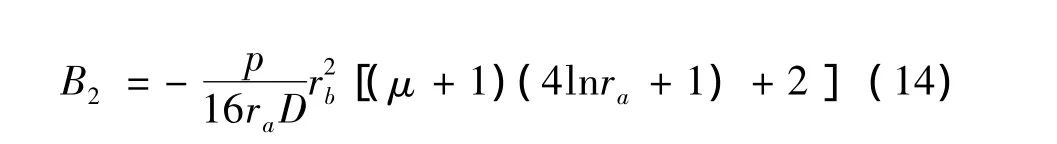
由式(4)～式(14)可计算出阀片在一定压力下任意半径r处的弯曲变形解析式fr。

2 减振器动力学分析与油液流动分析

油液在减振器内的流动有管嘴流动、薄壁小孔流动和缝隙流动，阀系内管嘴和小孔或缝隙间形成串联管路。

如图2所示，设上腔油液压强为Pr，下腔油液压强为Pc，储油腔油液压强为P0。

复原行程中，油液分二部分流动，一部分是油液由储油腔经底阀阀系流到下腔，另一部分是上腔油液经活塞阀系流到下腔。流经底阀阀系的油液，先流经底阀座补偿孔，设其节流压差为 P11，再流经补偿阀阀片和底阀座上凹槽两边凸起油线之间形成的内外两条缝隙，其节流压差为P12。流经活塞阀系的油液先流经活塞复原孔，其节流压差为P21，再流经活塞下端的复原阀节流孔(复原阀开启前)或节流阀片与活塞下端面油线间的缝隙(复原阀开启后)流入下腔，其节流压差分别为P22，P23。

压缩行程中，油液分二部分流动，一部分是油液由下腔经活塞阀系流到上腔，另一部分是下腔油液经底阀阀系流到储油腔。流经活塞阀系的油液，先流经活塞流通孔，其节流压差为P31，再经活塞上凹槽两边凸起油线和流通阀片之间的缝隙流入上腔，其节流压差为P32。流经底阀阀系的油液先流经底阀座压缩孔，其节流压差为P41，再流经底阀座下端的压缩阀节流孔(压缩阀开启前)或压缩阀阀片与底阀座下端面油线间的缝隙(压缩阀开启后)流入储油腔，其节流压差分别为 P42，P43。

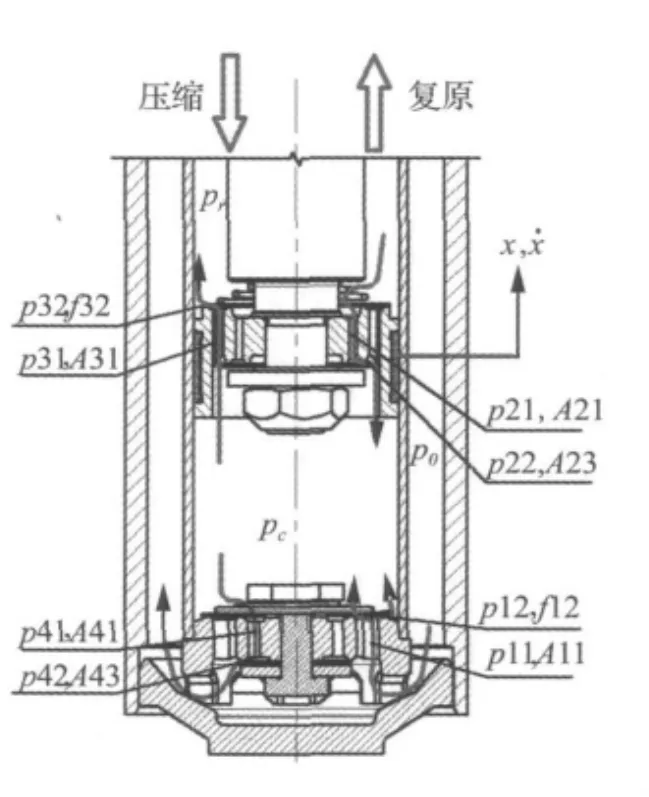
图2 复原及压缩行程中油液流动与压力的示意图Fig.2 Schematic diagram of the fluid flow and pressure during the rebound and compression strokes

2.1 减振器阻尼力的计算

减振器的阻尼力Fd由活塞上下两侧的压差所决定，如图2所示。

在复原行程中，由减振器活塞的受力关系可得:

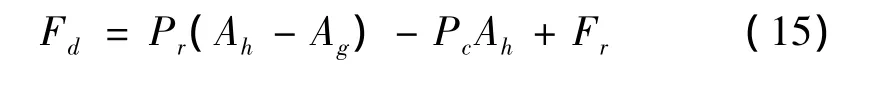
在压缩行程中，由减振器活塞的受力关系可得:

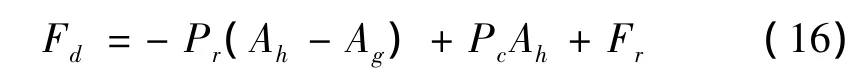
式中:Ah为活塞端面积;Ag为活塞杆的横截面积;Fr为活塞及活塞杆在运动过程中的摩擦力。

2.2 复原行程

复原行程中，设流经底阀阀系的流量为Q1，流经活塞阀系的流量为Q2。

2.2.1 底阀阀系压差的计算

在复原行程中底阀阀系上下总压差为:

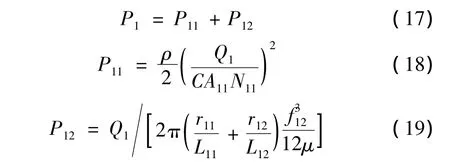
上式中:ρ为油液密度;C为压力损失系数，取0.82;A11为底阀座补偿孔截面积;N11为底阀座补偿孔数量;r11，r12分别为底阀座上凹槽的油线内、外半径;L11，L12分别为底阀座上凹槽两边凸起内、外油线宽度;f12为补偿阀阀片的开度;μ为油液的动力粘度。

由式(17)～式(19)可解出P1。

2.2.2 活塞阀系压差的计算

在复原行程中，活塞阀系上下总压差为:

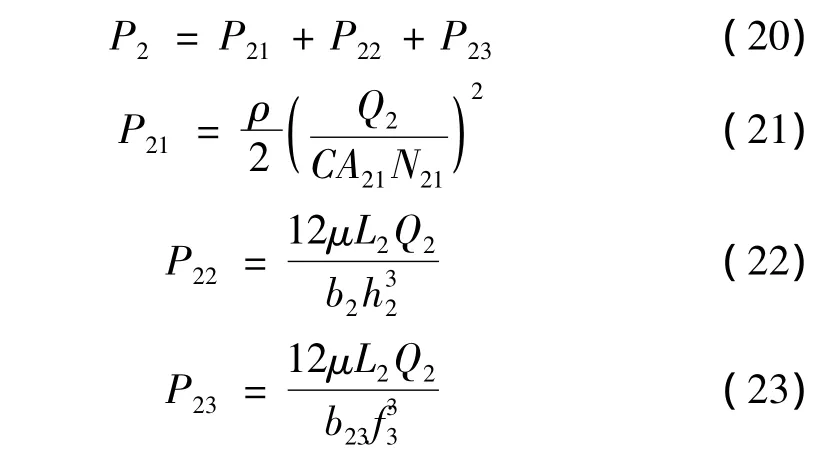
其中，复原阀开启前P23=0。

上式中:A21为活塞复原孔截面积;N21为活塞复原孔数量;h2为复原阀节流阀片缺口的高度;L2为与复原阀阀片接触的活塞下端面凸起油线宽度;b2为复原阀节流阀片缺口的总长度;b23为活塞下端凸起油线内圈周长;f3为复原阀的开度。

根据复原阀的结构参数，由式(4)～式(14)可求解出f3，然后再由式(18)～式(21)可解出 P2。则由式(15)可知复原阻尼力为:

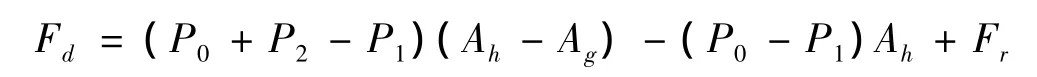
2.3 压缩行程

压缩行程中，设流经活塞阀系的流量为Q3，流经底阀阀系的流量为Q4。

2.3.1 活塞阀系压差的计算

在压缩行程中活塞阀系上下两端的总压差为:

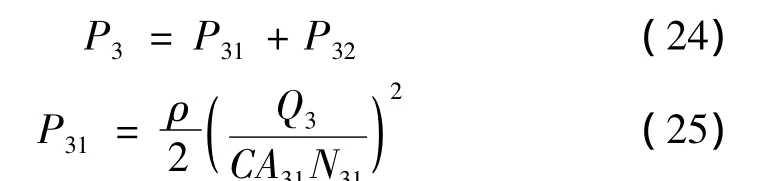
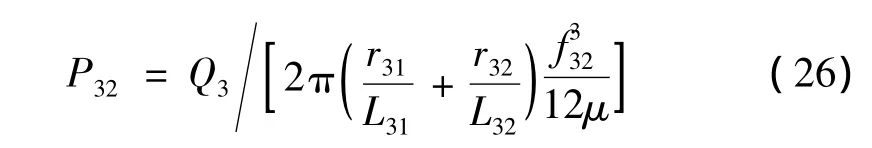
上式中:A31为活塞流通孔截面积;N31为活塞流通孔数量;r31，r32分别为活塞上凹槽的内、外半径;L31，L32分别为活塞上凹槽两边凸起内、外油线宽度;f32为流通阀的开度。

由式(24)～式(26)可解出P3。

2.3.2 底阀阀系压差的计算

在压缩行程中，底阀阀系上下总压差为:

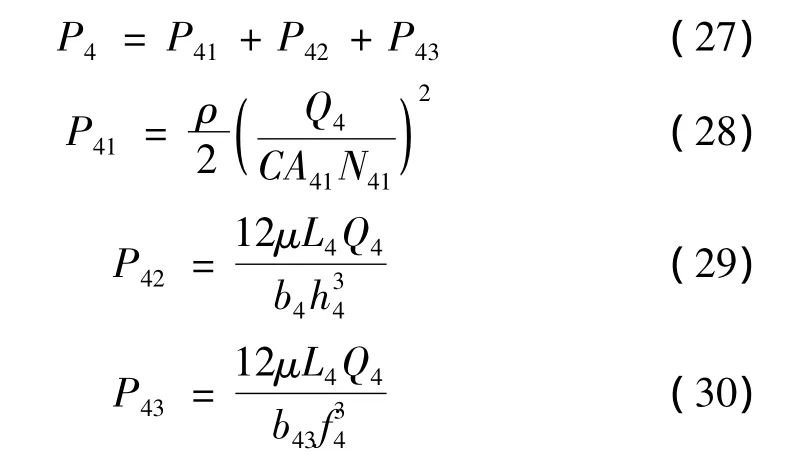
其中，压缩阀开启前P43=0。

上式中:A41为底阀座压缩孔截面积;N41为压缩孔数量;h4为压缩阀节流阀片缺口的高度;L4为与压缩阀阀片接触的底阀座下面凸起油线宽度;b4为压缩阀节流阀片缺口的总长度;b43为底阀座下端凸起油线内圈周长;f4为压缩阀的开度。

根据压缩阀的结构参数，由式(4)～式(14)可求解出f4，然后再由式(27)～式(30)可解出 P4。则由式(16)可知压缩阻尼力为:

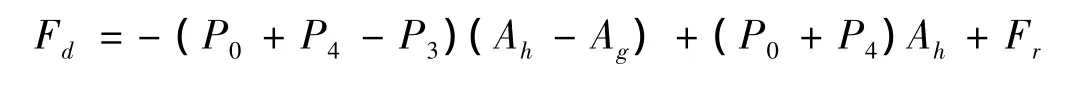
3 减振器外特性仿真与试验数据对比

根据减振器台架试验标准QC/T545，在减振器台架测试设备上采用正弦激励方式对减振器进行测试。

3.1 示功图(即力－位移曲线)

减振器阀系主要结构参数的设计数值见表1。

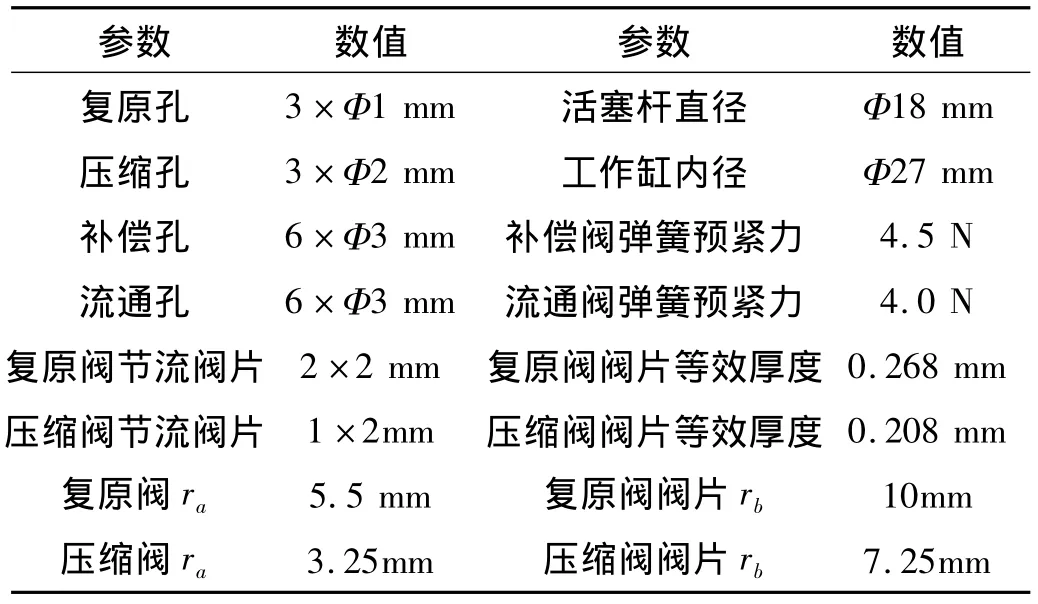
表1 减振器阀系参数Tab.1 Parameters of shock absorbers valve system

对减振器进行测试并仿真其示功图，测试行程为40mm，得到速度为 0.05，0.1，0.3，0.6，0.8，1.0(m/s)共六个速度点的示功图，如图3所示。

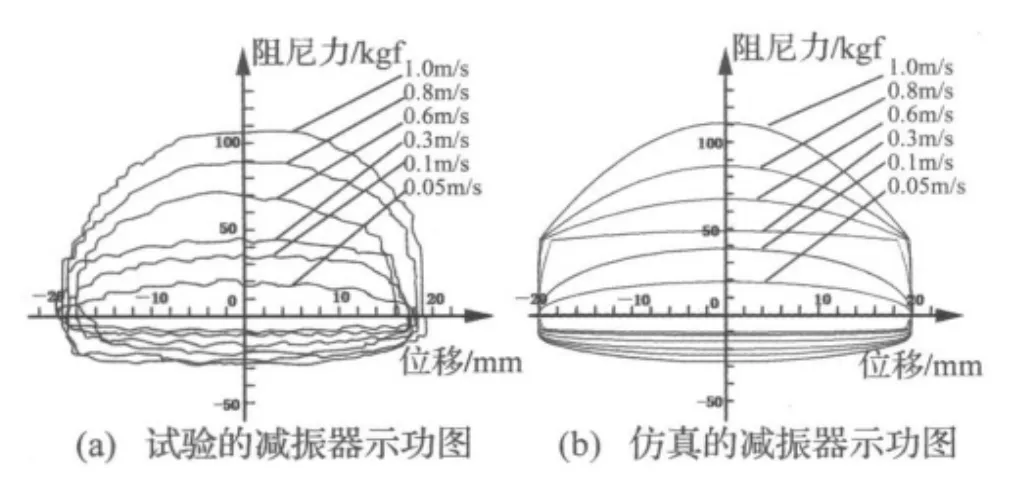
图3 试验与仿真的减振器示功图Fig.3 Experimental and simulation result of F-S curve

从上述示功图可看出:该减振器在各速度点的压缩阻力和复原阻力的示功图均饱满，无畸形;各速度点的复原及压缩阻尼力仿真与试验结果趋势一致，符合性较好，误差较小。证明在建模中考虑“补偿阀”及“流通阀”的影响并应用“受均布载荷作用的环形薄板阀片挠曲变形”理论及流体力学缝隙流动、管嘴流动及薄壁小孔节流理论建立的数学模型正确可靠。

3.2 速度特性曲线(力－速度曲线)

对该减振器进行测试并仿真其速度特性曲线，速度范围为50 mm/s～800 mm/s，测试及仿真结果如图4所示。

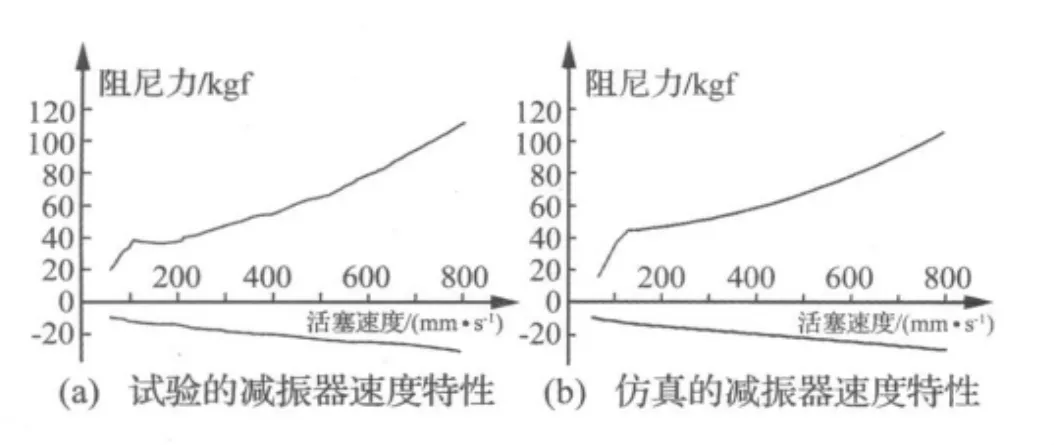
图4 试验与仿真的减振器速度特性Fig.4 Experimental and simulation result of F-V curve

从图中看出减振器的阻尼力随速度的增加而增加，模型仿真结果与试验结果趋势一致、符合较好。当速度达到120 mm/s左右时，试验及仿真的阻尼力有明显的突变，此点就是复原阀的开阀速度点，试验数据证明了仿真时对开阀速度的计算是准确的。

从上述仿真计算和试验结果来看，该减振器的示功特性及速度特性仿真结果都与其试验结果符合性较好，证明了本文提出的数学模型正确可靠。

4 补偿阀及流通阀对减振器阻尼力的影响

为了更准确地认识补偿阀及流通阀的作用，同时也为了更好、更方便地将此模型应用于工程设计并达到在设计过程中预测减振器外特性的目的，本文以下就补偿阀及流通阀参数对减振器阻尼力的影响及敏感程度进行了研究。

4.1 补偿阀及流通阀对阻尼力仿真结果的影响

以下就建模过程中考虑和不考虑“补偿阀”及“流通阀”这二种情况对所仿真的减振器阻尼力结果进行对比，其结果如图5所示。

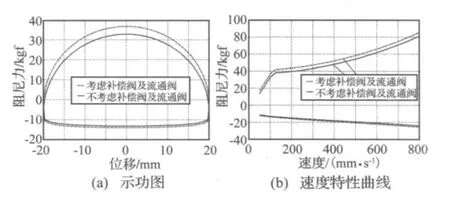
图5 补偿阀及流通阀对减振器仿真特性的影响Fig.5 The effects of the suction valve and intake valve on the shock absorber simulation characteristic

图5(a)是某一固定频率时，二种情况下的减振器示功图，由图中可看出，考虑“补偿阀”及“流通阀”时其仿真的复原及压缩阻尼力值比不考虑“补偿阀”及“流通阀”时要大。图5(b)是仿真二种情况时的速度特性曲线，从敏感程度来看，从低速到高速，二种情况对减振器的阻尼力的影响是一致的，是随活塞速度增加二者几乎平行的增大。

4.2 补偿阀及流通阀结构参数敏感性分析

运用上述所建立的减振器模型分别研究减振器“补偿阀”及“流通阀”阀系中其弹簧预紧力的大小、补偿孔和流通孔孔数对减振器阻尼力的影响，其仿真结果如图6所示。

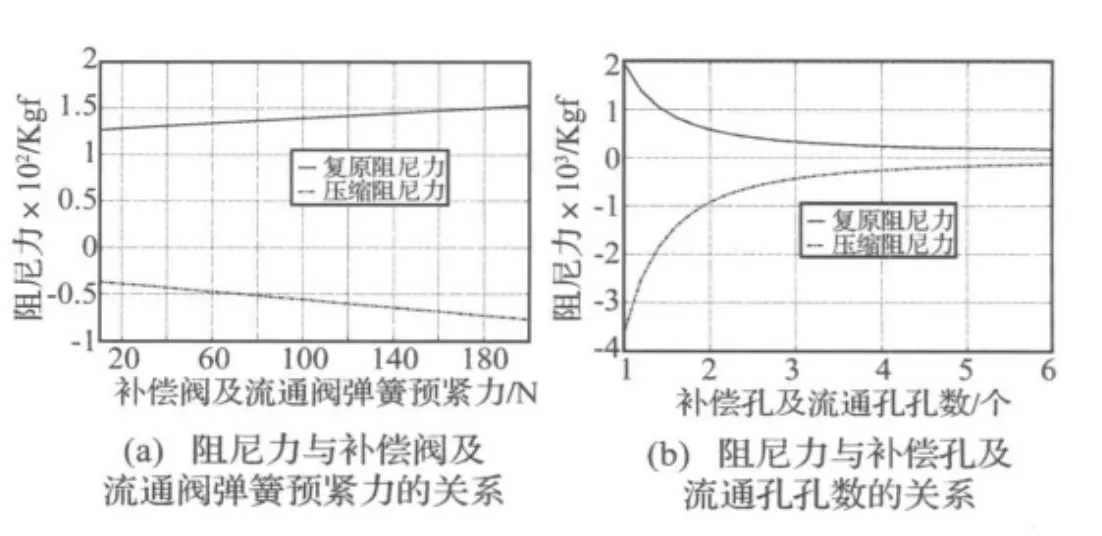
图6 补偿阀及流通阀对减振器特性的影响Fig.6 The effects of the suction valve and intake valve on the shock absorber characteristic

由图6(a)可知补偿阀及流通阀弹簧的预紧力越大，减振器阻尼力越大。就其敏感程度而言，其阻尼力与弹簧预紧力间基本上呈线性变化关系。由图6(b)可知补偿孔及流通孔孔数越多，减振器阻尼力越小。就其敏感程度而言，当孔数减少到一定值时，其阻尼力呈几何极数变化。因此，当“补偿阀”、“流通阀”的设计与复原阀和压缩阀的设计不匹配时，将会极大地影响到减振器的阻尼力，甚至出现示功图畸形。

5 结论

本文推导出了“受均布载荷作用的环形薄板阀片挠曲变形”微分方程，并用此方程得到了任意半径处的变形量;采用“受均布载荷作用的环形薄板阀片挠曲变形”方法，建立了汽车双筒式液压减振器的详细模型，模型中不仅应用了流体力学缝隙流动、管嘴流动、薄壁小孔节流理论，还考虑了流通阀、补偿阀对减振器阻尼力的影响;对所建立的数学模型采用MATLAB软件进行仿真研究，通过仿真得到了其外特性，将仿真结果和试验数据进行比较，二者符合较好，证明应用上述理论建立的数学模型正确可靠;应用所建立的数学模型，对比分析了在建模中考虑与不考虑“补偿阀”及“流通阀”这二种情况对仿真的减振器阻尼力的结果影响规律，同时还分析了“补偿阀”及“流通阀”阀系参数对减振器阻尼力的影响规律及敏感程度。这些复杂因素的考虑，使减振器阻尼特性的描述更为精确细致、能更准确地反映实际物理结构特性的规律，并为减振器的设计和性能预测提供参考。

［1］Duym S W R.Simulation tools，modelling and identification，for an automotive shock absorber in the context of vehicle dynamics［J］.International Journal of Vehicle Mechanics and Mobility，2000，33(4):261－285.

［2］Simms A，Crolla D.The influence of damper properties on vehicle dynamic behavior［J］. Society of Automotive Engineers，2002，1:79－86.

［3］Duym S W R，Reybrouck K.Physical characterization of nonlinear shock absorber dynamics［J］.Euro J Mech Eng M.1998，43:423－433.

［4］Lee K.Numerical modeling for the hydraulic performance prediction of automotive monotube dampers［J］.Vehicle System Dynamics.1997，28:25 －39.

［5］Besinger F H，Cebon D，Cole D J.Damper models for heavy vehicle-ride dynamics［J］.Vehicle System Dynamics，1995，24(1)，35–64.

［6］Zhou C C，Zheng Z Y，Zhang X Y.Design method for throttle holes area of telescopic shock absorber for small electric vehicles［J］.Journal of Asian Electric Vehicles，2009，7(1):1191－1197.

［7］周长城，顾 亮，王 丽.节流阀片弯曲变形与变形系数［J］.北京理工大学学报，2006，26(7)，581－584.

［8］陈轶杰，顾 亮，管继富.减振装置节流阀片均布载荷变形解析计算［J］.重庆大学学报，2008，31(9):988－991.

［9］周长城，顾 亮.筒式减振器叠加节流阀片开度与特性试验［J］.机械工程学报，2007，43(6):210 －215.

［10］Lee C T，Moon B Y.Simulation and experimental validation of vehicle dynamic characteristics for displacement-sensitive shock absorber using fluid-flow modelling［J］.Mechanical Systems and Signal Processing，2006，20:373－388.