纵向与横向振动耦合作用下轴向运动梁的非线性振动研究

黄建亮，陈树辉

(中山大学 应用力学与工程系，广州 510275)

传动系统广泛应用于各类工程领域中，例如磁带、空中缆车的缆绳、高速电梯绳、高速转动的锯片、动力传输带、造纸带等，它们的振动一直以来都是国内外研究的热点，大部分的模型可看作是轴向运动梁绳，属于经典的陀螺系统［1］。早期对该轴向运动系统的研究集中在线性振动问题的分析上，包含了固有频率、模态分析和运动临界速度等，然而线性振动分析解释不了振幅大或在临界速度附近出现的一些自激振动、参数振动、内共振、次谐波共振、超谐波共振、组合谐波共振、跳跃问题等非线性振动特有的现象，这些共振点会给工程设计带来隐患，仅研究线性问题无能为力，所以非常有必要考虑该类系统的非线性振动问题。

对轴向运动系统的非线性振动问题，国内外已有大量的文献报道。Wickert等［2］全面评论了至1988年以前的研究工作，Pellicano 等［3］和 Chen［4］分别在 2000年和2005对轴向运动系统的研究工作做了很好的综述。其中Riedel等［1］采用多尺度法研究了轴向运动体系的内部共振，Chen等［5］分析了粘弹性运动梁的横向振动的稳态响应，最近丁虎和陈立群对轴向变速运动黏弹性梁的受迫振动响应作了分析［6］。Öz等［7］研究了变速下运动梁的横向振动的稳定性问题。Sze等［8，9］应用IHB法研究了在恒定速度下运动梁的横向振动的基谐波、超谐波、次谐波等一系列复杂的稳态响应，陈树辉等［10］进一步研究了内部共振的情况，以及利用多元L－P法研究运动梁的横向非线性振动［11］。张伟等［12］分析具有Kelvin黏弹性材料的传动带，利用多尺度法和Galerkin离散法得到在1∶3内共振时平均方程，用数值模拟方法得到系统的周期振动和混沌动力学。由于运动梁的纵向振动频率远离横向振动频率，多数的研究都是直接忽略纵向振动对横向振动的影响。然而，在高速传动或振动幅度大时，纵向振动对系统振动响应的影响将不可忽略，并直接影响系统的内部共振特征。

本文探讨在纵向振动和横向振动耦合作用及受简谐外激励作用下轴向运动梁的非线性振动，应用IHB法深入分析在横向第1，2固有频率1∶3内部共振条件下系统的响应特征。

1 运动方程

图1所示为轴向运动梁的示意图，采用欧拉－伯努利梁力学模型。梁在两端铰支的条件下以轴向速度V运动，梁的横截面积为A，质量密度ρ，长度为L，抗弯刚度为EI，P为轴向张力，X为轴向坐标，XOZ是固定坐标系。记运动梁的横向位移为W(X，T)，纵向位移U(X，T)，T为时间。根据哈密顿原理(Hamilton’s Principle)建立梁的运动微分方程，得到下列无量纲化的纵向与横向耦合的非线性振动方程［8］:

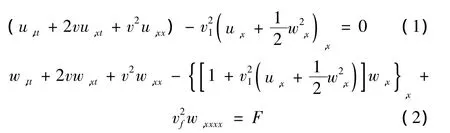
考虑运动梁两端为铰支，忽略支座处的弯矩，其边界条件为:

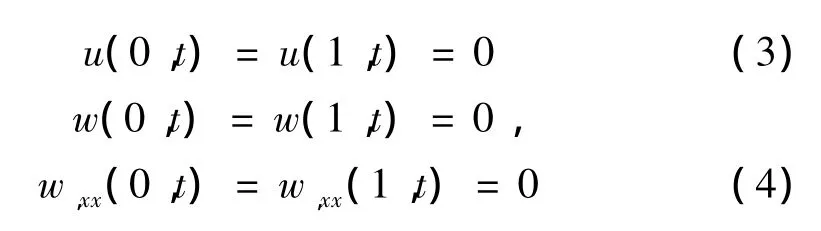
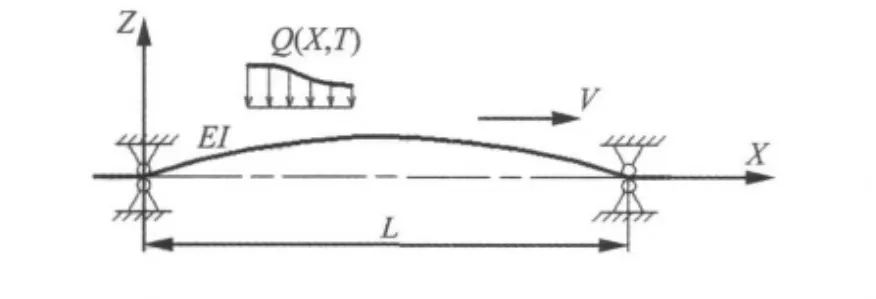
图1 运动梁的以速度V运动的示意图Fig.1 Schematic of an axially moving beam with velocity V

其中无量纲量:

2 Galerkin方法

首先采用变量分离，把时间变量t和空间变量x进行分离，为此，令:

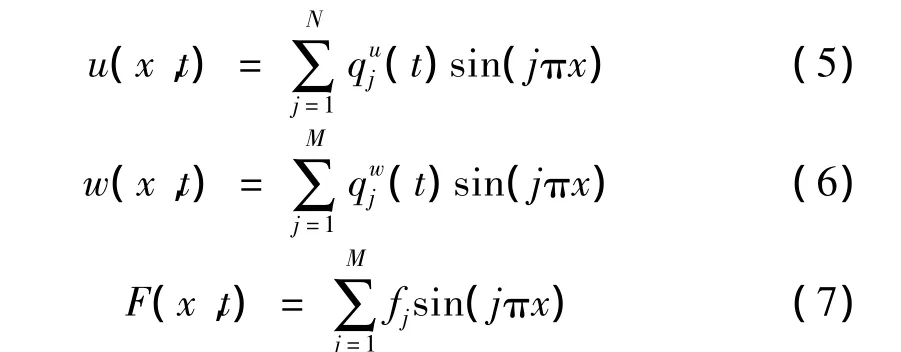
为简便计，只取N=M=2，将式(5)，式(6)和式(7)代入式(1)和式(2)后，应用Galerkin方法进行运算。在实际运动梁系统中存在着材料结构阻尼或粘弹性阻尼，为简单计，这里加入模态阻尼项μ，从而得到下列方程:

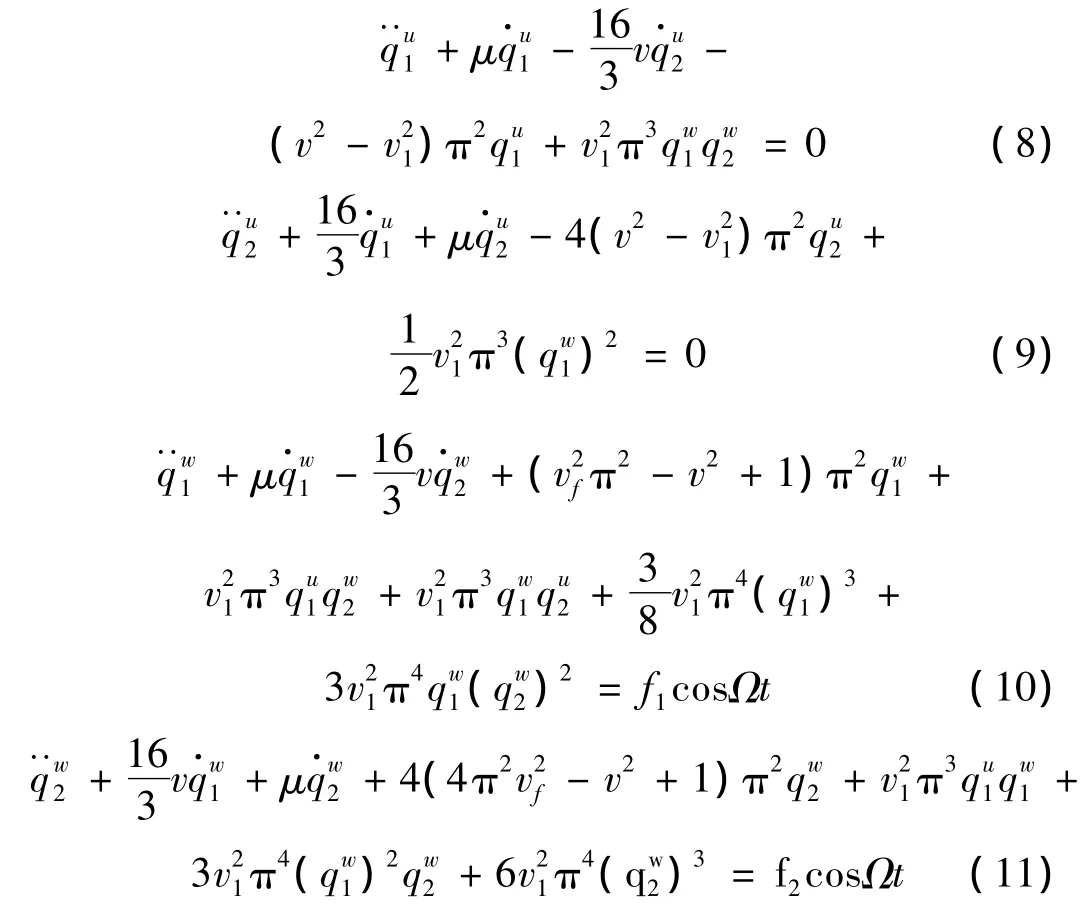
由方程(8)～方程(11)得知，阻尼矩阵具有反对称性质，所以该类系统具有陀螺特性，且方程中的恢复力包含了2次和3次非线性项。方程(8)和方程(9)及方程(10)和(11)可表示成矩阵形式:

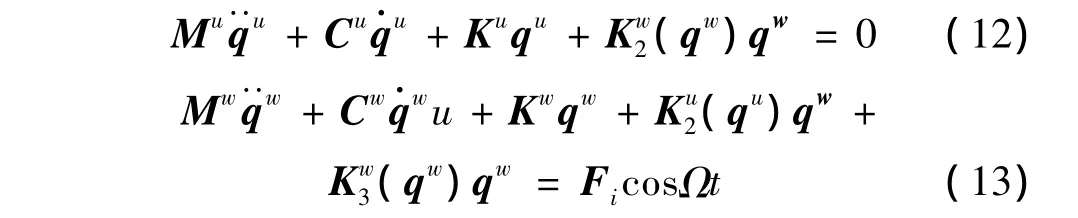
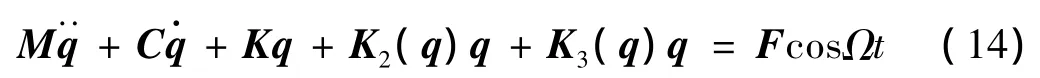
其中:

3 增量谐波平衡法(IHB法)

增量谐波平衡法(IHB法)自提出以来，在解决非线性振动的问题被广泛应用。Sze，陈树辉等［8，9］进一步推广到适合于含有陀螺系统特性的轴向运动梁的横向非线性振动。

引入新的时间变量τ，令:

方程(14)变为:

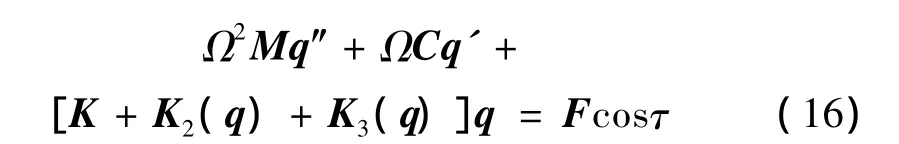
IHB法的第一步是Newton－Raphson的增量过程。令qj0和ω0表示振动过程中的某一状态，则其邻近的状态可以表示为增量的形式:

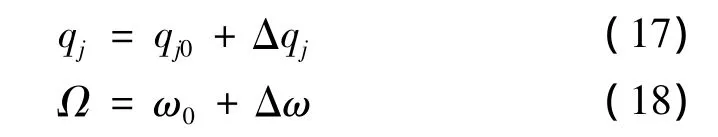
其中 j=1，2，…，m， m=N+M

将表达式(17)，(18)代入方程(16)并略去高阶项，便得到矩阵形式的增量方程:

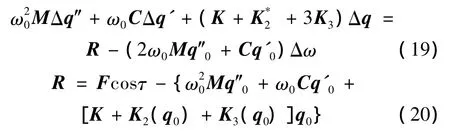
其中:

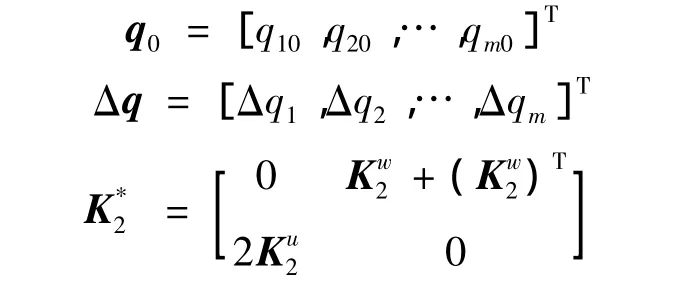
R是误差向量，当q0，ω0为准确解时，其值为零。

IHB法的第二步骤是谐波平衡过程。为此把q0和Δq展开成傅里叶级数:

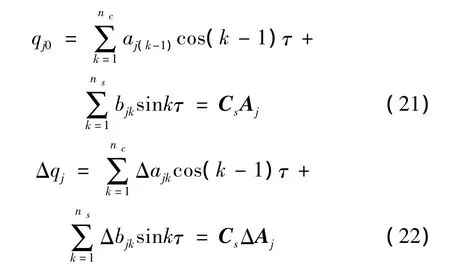
其中:

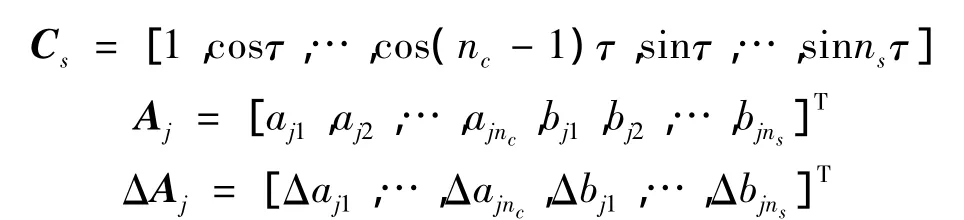
于是，

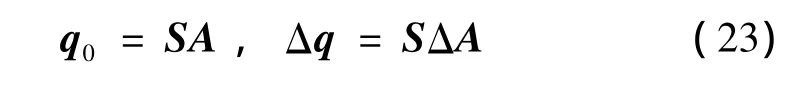
其中:

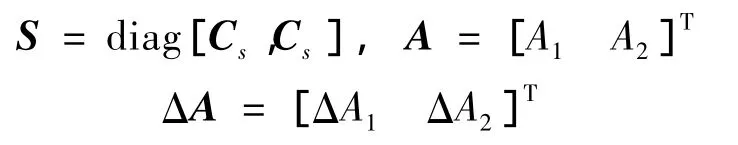
将式(23)代入公式(19)并应用Galerkin过程，可以得到以ΔA，Δω表示的线性方程组。

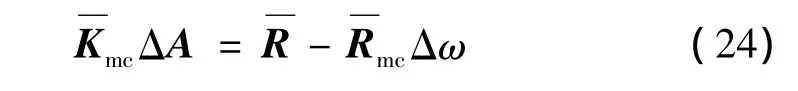
其中:

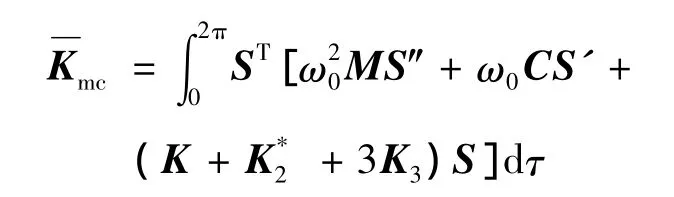
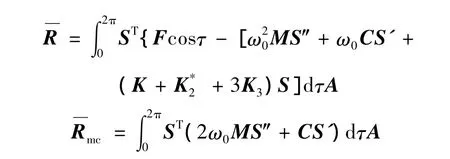
方程是一个线性方程组，其未知量的数目比方程数目多一个。因此，求解时必须选定其中一个增量作为控制增量。如果我们选择 Δω作为控制增量的话，则在给定的增量中，Δω是已知值，其他的增量从下列方程求解得到。

求得ΔA后，由表达式(16)求得Δq，q0，再由表达式求得q，从而求得新的，于是又可以从方程求得ΔA。这一过程称为迭代过程。迭代过程一直进行下去，直到误差向量R小于预先规定的误差值，此时就得到对应于Ω的振幅A，从而求得原方程的解。当迭代过程结束，再给控制增量Ω增加一个增量Δω，于是在新的Ω值之下进行上述的迭代过程，以求出对应新的Ω值的振幅A。这一人为给出增量Δω的过程称为Ω增量过程。整个非线性振动问题的求解过程就是反复交替应用增量过程和迭代过程。

4 算例

［1］所取的具有工程背景的参数=1124，=0.03，v=0.6。那么系统的固有频率可由方程(14)线性化后确定，表示为:

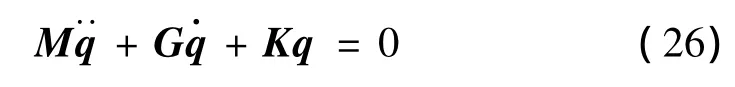
其中G为去除阻尼项之后的具有陀螺性质矩阵系数。

由式(26)得到横向振动的2个固有频率为2.82和 9.14，纵向振动的 2个固有频率为 105.29和210.65。纵向的前2阶模态的固有频率已远离横向的前2阶模态的固有频率，当横向振动幅度较小或轴向运动速度低时，纵向对横向振动的影响是有限的，然而不在上述情况时，我们不得不考虑两者耦合作用时的非线性振动。

在方程(21)中，取 nc=5，ns=4，令:

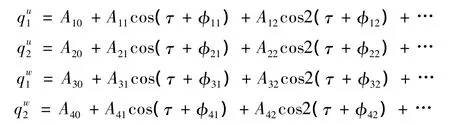
图2为横向振动的各阶频幅响应曲线图，实线和虚线分别表示为有无纵向振动影响下的响应曲线。从图中得知系统的呈现出硬弹簧特性，且Ω/ω1－A31的响应占主导地位，说明该系统的振动以横向的第一基谐波振动为主。图2(a)所示为横向振动的第一阶模态的频幅响应，当系统的振幅小时，纵向振动对横向振动的影响很小，而当振幅大时，纵向振动对横向振动的影响越来越明显，在同一频率处，在纵向振动的影响下，其横向振动的振幅要比没有耦合情况时要大，说明了纵向振动的能量向横向振动转移。但整个过程两者的非线性特性没有发生改变，在Ω/ω1≈1.2附近发生了内部共振现象，然而有耦合情况下，内部共振的特性更为复杂。图2(b)和(c)所示为横向振动第2阶模态的频幅响应，第1和第3谐波项响应较为接近。但因横向第2阶模态响应较小，所以纵向振动对它的影响非常大，图2(b)可看出其第1谐波响应的特性在纵向振动的影响下已完全改变;从图2(c)可看出在纵向振动的影响下第3 谐波响应分别在 Ω/ω1=1.14，1.25，1.62三个点趋于零，然而只考虑横向振动时没有出现该类现象。

图2 横向振动的频幅响应，f1=0.0055，f2=0Fig 2 .Frequency response of the first and third transverse mode with f1=0.0055，f2=0

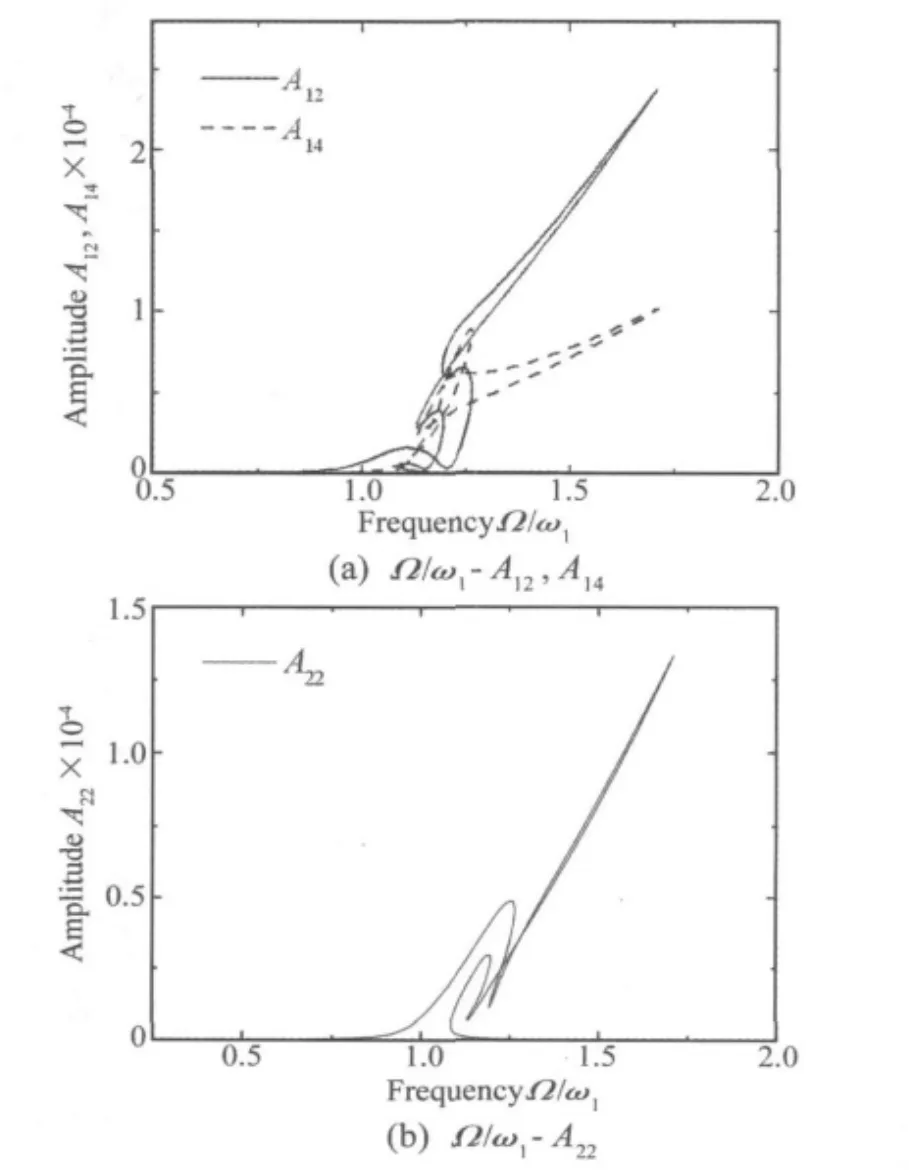
图3 纵向振动的频幅响应，f1=0.0055，f2=0Fig 3 .Frequency response of the first and third transverse mode with f1=0.0055，f2=0

图3所示为纵向振动各阶模态的频幅响应曲线图，图3(a)为第2，4阶模态各谐波响应，图3(b)为第2阶谐波响应(第4阶太小，未给出)。从图3得知，纵向振动响应远小于图2中的横向振动响应。其振动也呈现出硬弹簧特性，在Ω/ω1≈1.2附近也发生了复杂的内部共振现象。

5 结论

IHB法是一种十分有效的非线性动力学定量分析方法，应用该法对纵向振动与横向振动耦合时的横向两个模态之间1∶3的内部共振的运动梁的系统响应作了理论分析。纵向模态的频率虽然远离横向模态的频率，在只考虑横向振动的非线性特性时，为了进行简化，我们可先忽略纵向模态的影响。然而在纵向振动的影响下，横向振动其出现的内部共振现象更为复杂，在振幅较大时，纵向振动对横向振动的影响越来越大，且纵向模态的能量会向横向模态转移。所以设计高速传动的运动梁时，我们不得不考虑纵向模态与横向模态之间的耦合作用。

参考文献

［1］Riedel C H，Tan C A.Coupled，forced response of an axially moving strip with internal resonance［J］.Internal Journal of Non－linear Mechanics，2002，37:101 －116.

［2］Wickert J A，Mote Jr.C D，Linear transverse vibration of an axially moving string－particle system［J］.Journal of the Acoustic Society of America，1988，84:963－969.

［3］Pellicano F，Vestroni F，Nonlinear dynamics and bifuecations of an axially moving beam［J］.Journal of Vibration and Acoustics，2000，122:21 －30.

［4］Chen L Q.Analysis and control of transverse vibrations of axially moving strings［J］.Applied Mechanics Reviews，2005，58:91－116.

［5］Chen L Q，Yang X D.Steady－state response ofaxially moving viscoelastic beams with pulsating speed:comparison of two nonlinear models［J］.International Journal of Solids and Structures，2005，42:37 －50.

［6］丁 虎，陈立群.轴向运动黏弹性梁横向非线性受迫振动［J］.振动与冲击，2009，28(12):128－131.

［7］Öz H R，Pakdemirli M，Boyacm H.Non－linear vibrations and stability of an axially moving beam with time－dependent velocity［J］.International Journal of Non－Linear Mechanics，2001，36:107－115.

［8］Sze K Y，Chen S H，Huang J L.The incremental harmonic balance method for nonlinear vibration of axially moving beams［J］.Journal of Sound and Vibration，2005，281:611－626.

［9］陈树辉，黄建亮，佘锦炎.轴向运动梁横向非线性振动研究［J］.动力学与控制学报，2004，2(1):40－45.

［10］陈树辉，黄建亮.轴向运动梁横向非线性振动的内部共振研究［J］.力学学报，2005，37(1):57－63.

［11］Chen S H，Huang J L，Sze K Y.Multidimensional lindstedtpoincare method for nonlinear vibration of axially moving beams［J］.Journal of Sound and Vibration，2007，306(1 －2):1－11

［12］张 伟，温洪波，姚明辉.黏弹性传动带1∶3内共振时的周期和混沌运动［J］.力学学报，2004，36:443－454.