具有压电分流电路的声子晶体杆振动带隙研究

陈圣兵，韩小云，王 刚，温激鸿

(1.国防科技大学 机电工程研究所，长沙 410073;2.国家光子/声子晶体教育部重点实验室，长沙 410073)

声子晶体概念的提出为减振降噪理论研究和工程设计提供了新的思路。声子晶体是具有弹性波带隙的周期性结构功能材料，频率落在带隙范围内的振动会被禁止［1］。根据带隙频率所对应的波长与晶格常数的比例关系，声子晶体可分为Bragg散射型和局域共振型。局域共振型声子晶体中，单个散射体的共振特性起主导作用。通常是在基体材料中引入局域谐振子，通过振子的机械共振与基体中的长波行波相互耦合作用形成带隙。

随着智能材料的发展，将智能结构引入声子晶体，通过主动控制，使声子晶体的带隙可调，已经逐渐被人们重视。Ruzzene和Baz等人［2］首先将形状记忆合金引入到周期结构中，通过改变形状记忆合金的弹性模量来调节带隙。随后他们又将压电陶瓷材料及简单控制电路周期性地附加在一维杆［3，4］、管路［5－7］和二维周期弹簧质量系统［8］中，采用简单的控制电路，对周期结构的振动带隙进行调节。李凤明等［9，10］采用传递矩阵法研究了周期嵌有压电材料的杆和梁结构中的波动传播特性及其振动主动控制问题。张文群等［11］研究了负电容压电分流阻尼系统的能量耗散特性，分析了不同连接方式电路的特点。孙浩和杨智春等［12］也对压电分流阻尼系统中压电片的拓扑优化做了较为深入的研究。

本文提出在基体杆上周期性粘贴连有分流电路的压电片，用分流电路中LC回路的电磁振荡代替局域共振声子晶体中传统机械局域谐振子的振动。利用压电片的机电转换能力和LC电路的谐振特性设计了局域共振声子晶体杆结构，运用传递矩阵法计算了杆的带隙结构，并分析了杆的带隙形成机理以及在LC电路中引入耗散电阻后对带隙的影响。最后，采用商用有限元分析软件ANSYS中的压电模块和电路模块对杆的振动特性进行了仿真计算。

1 声子晶体杆振动的波动模型

声子晶体杆的结构如图1所示。在基体杆上周期性对贴压电陶瓷片，形成周期结构。因为压电陶瓷片本身存在电容，所以采用并联电容分流电路可以使振荡电路中总电容等于外接电容和压电片电容之和，与串联电容分流电路相比，可以有效增大电路中总电容的调节范围，而且可以使电路固有振荡频率与电容的调节关系更直观。所以将压电陶瓷片与电容C、电感L和电阻R并联，形成并联分流电路。

图1 周期杆示意图Fig.1 Schematic diagram of periodic rod

图2 压电分流电路Fig.2 Piezoelectric shunting circuit

1.1 压电方程和杆的结构动力学方程

压电分流电路如图2所示，假设压电片除去沿长度的两端外其余表面均自由，且压电片只受沿厚度方向的电场作用，则d－型压电方程简化为［13］:

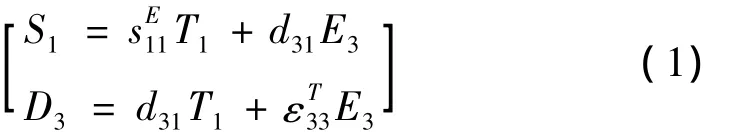
其中T1、S1为压电片在长度方向的应力和应变，D3为压电片厚度方向表面电位移，E3为压电片在厚度方向的电场强度，为弹性柔顺常数，为厚度方向恒应力介电常数，d31为压电常数。

将电场和电位移公式代入方程(1)解得［4］:

其中:s为拉普拉斯算子，As为压电片电极面积，hp为压电片厚度，Cp为压电片电容，

将s=iω代入式(2)得简谐振动下压电片应力与应变的关系为:

其中i为虚数单位，ω为振荡频率。

即在分流电路作用下，压电片的等效弹性模量变为:

其中Cto为电路中总电容，Cto=C+Cp。

取杆的一个基本周期单元，如图3所示。基体杆的截面为矩形，厚度为hb，宽度为lb，截面面积为Ab，弹性模量为Eb，密度为ρb;压电片的长度为b，宽度为lp，截面面积为Ap，密度为ρp。M表示未贴压电片的杆，N表示贴有压电片的杆。设y(x，t)为杆在x处的振动位移，则杆的振动方程为［14］:

式中:ρ、E为杆x处的密度和弹性模量，y为杆x处的振动位移，y=X(x)eiωt。

图3 单个周期单元Fig.3 Sketch map of the cell

由方程(5)解得，杆的第n个周期单元中M部分的振动幅值在局部坐标系下为:

其中:

杆的第n个周期单元中N部分振动幅值在局部坐标系下为:

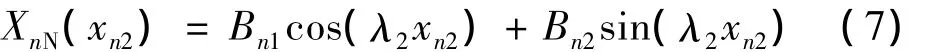
其中:

1.2 杆单元的边界条件

在周期单元n中N部分的左边界处，位移X(x)、力EAX'(x)的连续性可得:

整理为矩阵形式为:

式中 ψn=［An1An2］T，γn=［Bn1Bn2］T。

在周期单元 n中 N的右边界处，位移X(x)、力EAX'(x)的连续性可得:

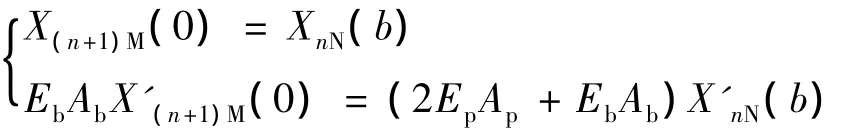
整理为矩阵形式为:

式中:ψn=［A(n+1)1A(n+1)2］T，γn=［Bn1Bn2］T。

将式(8)代入式(9)得:

1.3 杆中波传播的动力学特性

杆是由相同的周期单元组成的，根据 Bloch定理［15］:

其中μ为波传播常数。

将式(10)代入式(11)得特征值方程:

其中:I为单位矩阵。

由方程可得，对于给定频率ω，可以求出波传播常数μ。当频率位于某些范围时，波传播常数实部为零，这表明周期杆中这些频率范围内的弹性波将无衰减传播。而波传播常数实部不为零时，周期杆中弹性波仅存在衰减的传播模式，这些频率范围形成带隙。

1.4 杆中局域共振带隙形成机理研究

压电片与分流电路相互作用，其等效刚度变为式(4)所示，整理为:

则杆上贴有压电片的N部分的等效弹性模量为:

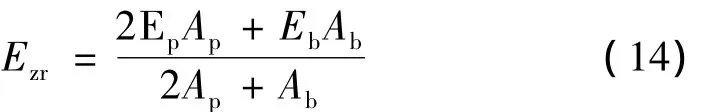
联立式(13)、式(14)得，当 ω =ωzr时，Re(Ezr)=0。

式中:ω0—— 分流电路固有频率。

此时杆中N部分的等效弹性模量实部为0，那么弹性波显然不能在杆中传播，必然形成带隙。因此杆的局域共振带隙在ωzr处，比电路振荡固有频率高。

2 数值计算结果

基体杆的材料选用环氧树脂，其弹性模量Eb=4.35 ×1010Pa，密度为 ρb=1180 kg/m3，厚度为 hb=0.01 m，宽度 lb=0.02 m，a=0.03 m，b=0.04 m。压电陶瓷片选用 P ZT －5H，d31= －274×10－12C/m2，=3.01 × 10－8F/m，=16.5 ×10－12m2/N，厚度 hp=0.0005 m，lp=0.02 m。

2.1 杆的带隙结构

由以上参数仿真计算得到杆的带隙结构如图4所示。图4(a)为电感L=0，R=10 Ω时的带隙结构，此时分流电路不能产生电磁振荡，其带隙由压电陶瓷片与基体杆间的Bragg散射引起，为Bragg带隙。图4(b)为电感 L=7 ×10－3H，C=0，R=10 Ω 即 Cto=Cp时的带隙结构，此时分流电路中能产生电磁振荡，其带隙包括局域共振带隙和Bragg带隙。

图4 杆的带隙结构Fig.4 Band gaps of the rod

2.2 电感、电容和电阻对局域共振带隙的影响

从式(15)可以看出，调节分流电路中电感L和电容C的值，可改变局域共振带隙位置，如图5所示。图5(a)为带隙随电感L的变化，局域共振带隙频率随着电感值的增大而降低。当L=3×10－3H时，局域共振带隙和Bragg带隙位置重合，合并为一个带隙。图5(b)为带隙随电容的变化，局域共振带隙频率也是随着电容值的增大而降低。

图6为带隙随电阻的变化，从图中可以看出随着电阻的增大局域共振带隙衰减幅值是逐渐减小的，因为电阻的增大会使电路中电流减小，减弱了LC回路的电磁振荡作用或者说振荡回路的Q值下降。

为了验证理论计算的正确性，利用ANSYS有限元软件对有限周期的杆进行了有限元计算。取6个周期进行有限元计算，其中基体杆用solid45单元进行网格划分，压电陶瓷片采用solid5单元，电感和电容采用circuit94单元。在杆没有粘贴压电片的一端以恒定位移1×10－5m进行激励，利用ANSYS的谐响应分析进行有限元计算，得到振动在杆中传到另一端的位移响应如图7 所示，其中 R=10 Ω，C=0，L=7 ×10－3H。

从ANSYS有限元计算结果可以看出在8980 Hz～9520 Hz出现了局域共振带隙，与图4所示的理论计算结果基本一致。

图5 带隙随电感和电容的变化Fig.5 Band gaps’variations with the inductance and capacitance

图6 带隙随电阻的变化Fig.6 Band gaps’variations with the resistance

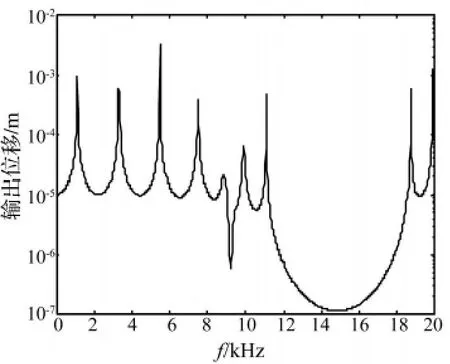
图7 ANSYS计算传输特性Fig.7 Transmission properties calculated by ANSYS

3 结论

通过对含有压电分流电路声子晶体杆的理论计算和ANSYS分析可以得到以下结论:

(1)杆的带隙是Bragg散射和局域共振共同产生。当分流电路中电感等于零时，电路中不能产生电磁振荡，带隙由基体梁与压电片之间的Bragg散射形成，为Bragg带隙。当分流电路中电感不等于零时，分流电路的电磁振荡会形成局域共振，产生局域共振带隙。

(2)局域共振带隙的带隙频率为贴有压电片部分等效弹性模量实部为零所对应的频率，比分流电路的固有频率略高。通过改变电容和电感参数，可以调节局域共振带隙的位置。

(3)分流电路中的耗散电阻会使电路中电流减小，电磁振荡变弱即振荡回路的Q值下降，从而减小了局域共振带隙在带隙频率内的振动幅值、增加了带宽。

总之，利用压电材料的机电转换作用，激励分流电路，通过电磁振荡形成局域共振，为局域共振型声子晶体设计提供了新的思路。与传统机械振子局域共振声子晶体相比，由于分流电路中电感、电容和电阻可以方便的调节，因而可以根据需要主动控制局域共振带隙频率的位置。而且分流电路不参与杆的机械振动，减小了振动结构的质量。

［1］温熙森.光子/声子晶体理论与技术［M］.北京:科学出版社，2006.

［2］Ruzzene M，Baz A.Attenuation and localization of wave propagation in periodic using shape memory inserts［C］.Proceedings of SPIE，2000，3991:389－407.

［3］Baz A.Active control of periodic structures［J］.J.Vibration and Acoustics，2001，123:472－479.

［4］ThorpO，Ruzzene M，Baz A.Attenuation and localization of wave propagation in rods with periodic shunted piezoelectric patches［C］.Proceedings of SPIE，2001，4331:218 －238.

［5］Ruzzene M.Active control of wave propagation in periodic fluid-loaded shells［J］.Smart Materials and Structures，2001，10:893－906.

［6］Ruzzene M，Gu Z，Baz A M.Wavelet analysis of wave propagation in shells with periodic stiffeners［C］.Smart Structures and Materials 2001:SmartStructures and Integrated Systems，Newport Beach，CA，USA，2001.

［7］Thorp O， RuzzeneM， BazA. Attenuation ofwave propagation in fluid-loaded shells with periodic shunted piezoelectric rings［J］.Smart Materials and Structures，2005，14:594－604.

［8］Kim Y，Baz A M.Active control of a two-dimensional periodic structure［C］.Smart Structures and Materials 2004:Damping and Isolation.Proceedings of the SPIE，2004，5386:329－339.

［9］李凤明，汪越胜.压电周期结构振动主动控制研究［J］.振动工程学报，2004，17:828－830.

［10］Chen A L，Li F M.Localization of flexural waves in disordered periodic piezoelectric beam［J］.Journal of Sound and Vibration，2007，304:863 －874.

［11］张文群，张 萌，吴新跃.负电容压电分流阻尼系统的能量耗散特性［J］.振动与冲击，2008，27(10):70－73.

［12］Sun H，Yang Z C，Li K X，et al.Vibration suppression of a hard disk driver actuator arm using piezoelectric shunt damping with a topology-optimized PZT transducer［J］.Smart Materials and Structures，2009，18:1－13.

［13］栾桂冬，张金铎，王仁乾.压电换能器和换能器阵［M］.北京:北京大学出版社，2005.

［14］温激鸿.声子晶体振动带隙及减振特性研究［D］.长沙:国防科技大学，2005.

［15］温激鸿，郁殿龙，等.周期结构细直梁弯曲振动中的振动带隙［J］.机械工程学报，2005，41(4):1－7.