基于蠕动泵的注排液式转子自动平衡实验研究

李 燕，王维民，黄立权，高金吉

(北京化工大学 诊断与自愈工程研究中心，北京 100029)

不平衡是导致转子振动故障的主要原因，这类故障严重影响了设备的生产效率和使用寿命。传统的平衡方法是对转子进行离线平衡，这在一定程度上增加了维修开销。转子在线平衡系统不但能够及时降低振动，而且能够在设备的长期运转过程中调整不平衡状态，从而保持设备的良好运转过程。目前应用的主要在线平衡系统分为两类，一类是电磁式平衡系统［1－5］，另一类是注液式平衡系统［6－9］。注液式自动平衡系统的原理是利用调整平衡盘上的多个腔内的液体来补偿转子的不平衡，每一个腔体对应不同的注液孔，注液孔通过电磁阀进行控制。系统根据转子不平衡情况向不同腔内注入不同质量的液体，以改变平衡头的重心位置，达到在线平衡。但是常规的平衡盘及传统注液算法存在两个缺点，一是常规注液式平衡盘在工作一段时间后由于液体无法排出会失去平衡能力。针对这一问题，高金吉、张鹏等［10］设计了连续注排式自动平衡装置。该平衡盘在各个腔室外沿设计有排液小孔，在设备运行时，液体会由于离心力而被排出平衡盘。通过不受控的排液和可控的注液来控制腔内的液体容量，从而避免了平衡盘容腔被注满失去平衡能力的缺陷。二是传统的注液算法常会出现首次注液振动增大的情况，这种瞬时的振动突增危险性更大，本文的研究内容解决了这一问题。另外，传统单注液式平衡系统采用的电磁阀在工作过程中开关频繁，容易造成故障，使设备无法正常工作，为解决这一隐患，利用多台蠕动泵研制了流量控制系统，提高了系统的可靠性。

使用连续注排液式平衡盘，构建转子振动在线实时自愈系统。利用矢量平衡法计算转子的振动和不平衡量的关系，从而能够将测得的振动准确的转换为转子上的不平衡量，使注液系统能够准确的注液，避免了首次注液振动会增大的情况。并且该系统具备单注液式和注排液式两种工作模式，对于振动变化比较剧烈的设备，可以选择注排液式;对于振动变化不大的设备，可以选择单注液式的工作模式。

1 转子不平衡响应特性及控制策略

以超重力机悬臂转子为研究对象，构建实验装置，研究转子的不平衡响应。实验室用超重力机是一台由于振动问题无法正常进行生产的设备，其结构如图1所示。其物料盘直径为450 mm，据用户报告运行一段时间后会产生1000 g左右的残留物质，因此最大可能产生225000 g·mm的不平衡量。超重力机转子工作转速为1495 r/min，通过有限元方法计算其一阶临界转速为3810 r/min，因此可以将此转子看为刚性转子。在此转子上加上一定的配重后，会产生一定的不平衡响应，对于转速稳定的转子来说，可以计算不平衡量和响应之间对应关系即影响系数k。方法如下:

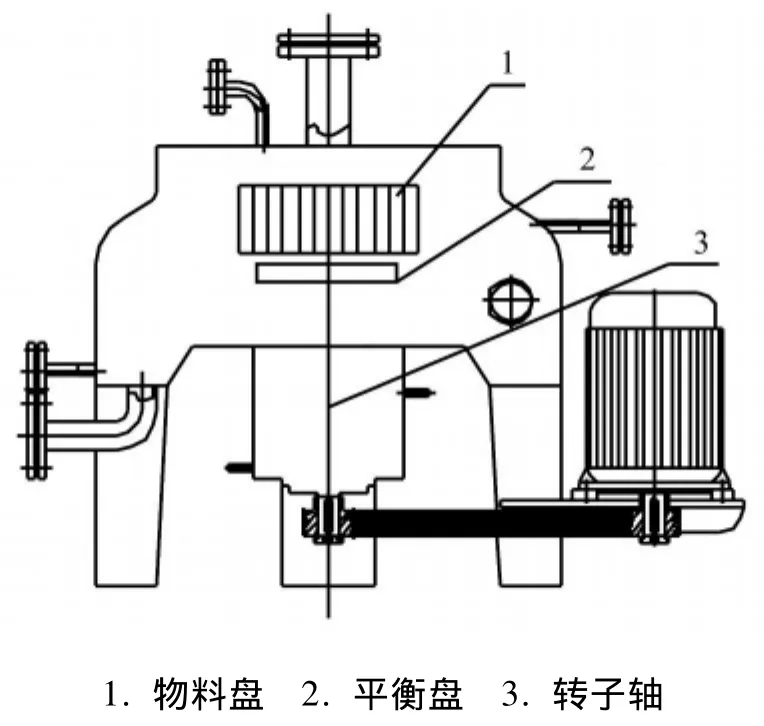
图1 超重力机转子示意图Fig.1 The diagram of the high-gravity machine

可计算 。得到影响系数k值后，系统就可以将实时振动信号转为不平衡量。

根据刚性转子的平衡方法，只需知道转子不平衡量的振幅和相位，即可通过质量补偿，消除振动。则消除振动所需要的配重为:

在得到转子不平衡量之后，即可以通过注液将不平衡量消除。

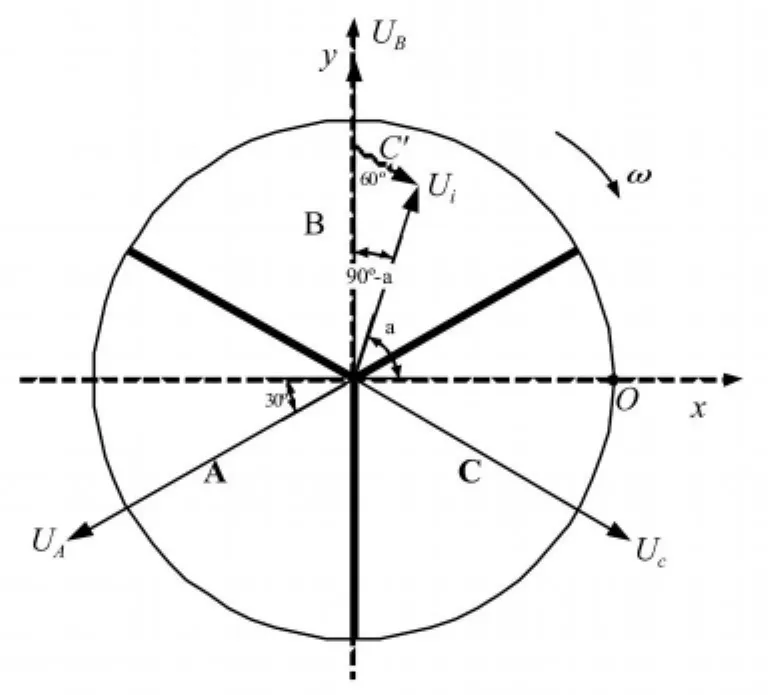
图2 不平衡量的消除计算示意图Fig.2 The computational diagram of unbalance mass

因为Ug和α已知，因此可以求出B和C腔内应注入的液体量，当落在其他位置时，也可以根据余弦定理求出。

将平衡盘紧靠在物料盘下方安装，并使平衡盘C腔区域内O点处与转子轴的键相槽相对应，O点是物理0°点，测得的相位也是以此点为基准。

对于某一扇形夹角为θ，厚度为h的扇形空腔储液室，其中液体可产生的质量不平衡矢量U可通过积分算得，如图3所示。对于半径在r到r+dr范围，角度在α到α+dα范围内(以扇形角θ平分线方向向外为0°)的一微元体积 M ，其重量为(rdα)drhρ，其不平衡量为［(rdα)drhρ］r，则对于为液面所处位置的半径)范围内的储液室可产生的总不平衡量可得:

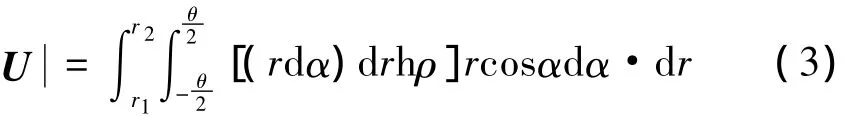
从式(4)可以看到腔的平衡能力是由当前液面r1决定的，设备运行时，平衡盘腔内的液面难以测量，而平衡盘的排液速度是一定的，因此可以通过控制进液速度来得到式(3)计算所得的各腔的平衡质量。

图3 储液室平衡能力的计算Fig.3 Correction capacity of a chamber

2 转子振动自愈系统

2.1 流量控制系统

传统的注液式转子振动系统的注液部分多采用电磁阀或者阀组来实现流量控制，采用阀有两个缺点，一是小流量控制时，由于加工精度等影响，流量控制不精确;另一缺点是电磁阀在平衡过程中开关比较频繁，易发生故障，当某一路电磁阀出现故障时，系统将无法工作。因此考虑使用蠕动泵组来实现流量精确控制，并采用故障代偿的方法使流量控制系统具备故障自愈能力。

图4 蠕动泵组流量控制系统结构框图Fig.4 The structure of liquid control system with peristaltic pump

图4是针对三腔式平衡头设计的蠕动泵组流量控制系统，由三台蠕动泵组成，分别向平衡盘的三个腔内注液，每相邻两路注液管用装有电磁阀的管道连接，并且三路注液管中安装有电磁阀和流量测量装置。计算机通过串口对蠕动泵进行控制，通过数字量I/O卡控制电磁阀的开关状态。在正常工作状态下，两台蠕动泵工作，一台后备，系统会实时判断管道中的流量是否和应该输出的流量一致，如果误差大于5%，则可判断该路蠕动泵出现故障;设图4种1号，3号蠕动泵正常工作，1号泵突然发生故障，此时系统会驱动2号泵工作，并同时打开2号泵和1号泵之间连通管道的电磁阀，关闭2号泵本身注液管道的电磁阀，实现系统的稳定可靠运行。

2.2 振动自愈系统

图5是转子振动自愈系统框图。其中UA、UB和UC为平衡盘3个腔体注液矢量，fa、fb和fc为注液量。由于超重力机转子的振动变化比较剧烈，因此选用连续注排液的工作模式。图6是流量控制系统及实验台转子及测量装置和平衡盘的安装图。

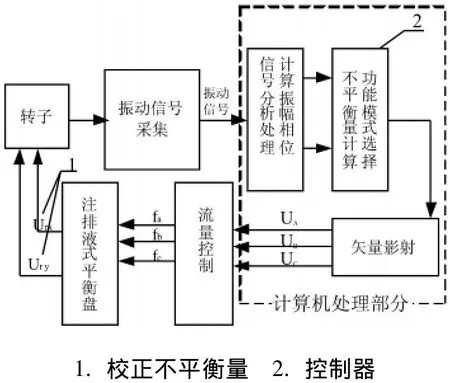
图5 超重力机振动自愈系统框图Fig.5 The structure of rotor vibration self-recovering system

3 振动控制实验

(1)以物料盘转轴键相槽所处位置为0°点，在135°，半径220 mm的地方加配重62.5 g，振动自愈调控结果如图7中曲线1所示;

图6 超重力机振动自愈调控实验台Fig.6 The experiment high-gravity machine

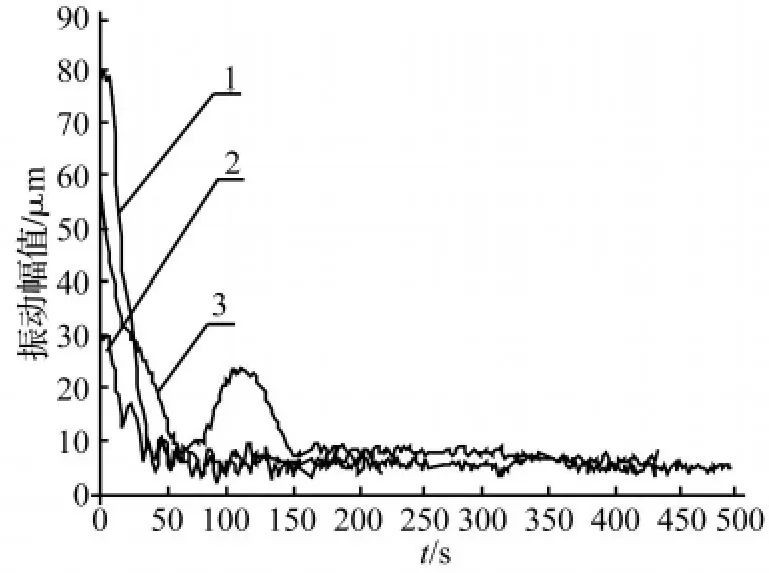
图7 转子振动幅值控制曲线Fig.7 The vibration curve in control

(2)以物料盘转轴键相槽所处位置为0°点，在22.5°，半径 180 mm 的地方加配重 47.5 g，振动自愈调控结果如图7中曲线2所示;

(3)以物料盘转轴键相槽所处位置为0°点，在物料盘上方安装2个配重支架，2个配重螺丝通过棉线连接，棉线中间夹一段蚊香，点燃后启动设备，一段时间后棉线被烧断，配重螺丝产生瞬时不平衡量，振动自愈调控结果如图7中曲线3所示。

从图7中，使用连续注排式平衡盘的振动自愈系统能在50 s内将振动减小10 μm左右，对于瞬时变化的振动也能快速反应，将振动保持在比较小的范围内。长时间实验显示，在平衡盘的平衡能力范围内，可以将振动控制在10 μm以下。

4 结论

(1)实验研究结果表明，连续注排液自动平衡装置能解决常规注液平衡盘因腔被注满而失去平衡能力的问题，有效延长设备的生产周期，提高生产效率，减少维修成本，而且不会产生首次注液加大振动的故障。

(2)通过在多角度加配重以模拟不同相位的振动的实验研究，表明该系统能够对各个相位的不平衡量进行快速消除，平衡效果明显。

(3)该系统能够对瞬时振动变化快速响应，从而快速有效地缓解或避免由于瞬时不平衡造成的危害，具有很好的工程实用价值。

(4)蠕动泵组式流量控制系统具有流量控制精确、扩容简单，可靠性高、易于实现液体循环使用和故障自愈等优点。

通过超重力机振动自愈调控系统的实现，证明了连续注排液式平衡盘能够长时间的保持平衡能力，有效减少转子的振动。这些实验数据为进一步提高其平衡效率和实际应用奠定了基础。

［1］Shin K K，Ni J.Adaptive control of multi-plane active balancing systems for speed-varying rotors［J］.Journal of Dynamic Systems，Measurement，Control，2003，125(3):372－381.

［2］Dyer S W ，Ni J，Shi J J.Robust optimal influence-coeffcient control of multiple-plane active rotor balancing systems［J］.Journal of Dynamic Systems，Measurement and Control，2002，124(1):41－46.

［3］Shin K K.Adaptive control of multi-plane active balancing systems for speed-varying rotors［J］.Journal of Dynamic Systems，Measurement and Control，2003，125(3):372 －381.

［4］Delvaux S，Van B M.Rank structures preserved by the QRalgorithm:The singular case［J］.Journal of Computational and Applied Mathematics.2006，189(1):157 －178，

［5］Zhou S，Dyer S W，Shin K K.Extended influence coefficient method for rotor active balancing during acceleration［J］.Journal of Dynamic Systems， Measurement and Control，2004，126(1):219 －223.

［6］李长河，原所先，修世超，等.超高速磨削中的砂轮自动平衡技术［J］.新技术新工艺，2004，5:29－31.

［7］余鹤轩.微机控制砂轮液体动态平衡装置的研制［J］.磨床与磨削，1989，1:13 －17.

［8］母德强，赵心文，毛志阳，等.径注式砂轮在线液体平衡装置的设计［J］.中国机械工程，1996，7(3):58－59.

［9］贺世正.释放液体式自动平衡头的研究［J］.浙江大学学报，2001，35(4):418－422.

［10］Gao Jinji， Zhang Peng. Simulativestudyofautomatic balancing of grinding wheel using a continuously-dripping liquid-injection balancing head［C］//WCICA 06，The Sixth World Congress on Intelligent Control and Automation，IEEE Press，DaLian，2006，2:8002 －8005.