基于比例风险模型的板级无铅焊点跌落寿命分析

王 文，孟 光，刘 芳，尤明懿

(上海交通大学 机械系统与振动国家重点实验室，上海 200240)

随着手提式、便携式电子产品的广泛使用，并朝着多用途、多功能化发展，使得电子封装设计趋向高密度、小尺寸，这使得焊点的跌落可靠性问题变得越来越突出。跌落碰撞不仅会导致电子产品外壳的机械损坏，而且由于能量的传递与转化，依附于外壳上电路板(printed circuit board，简称:PCB)的电子元器件及其不同部位的焊点由于受到变化的应力应变也会发生失效破坏，轻则造成电子产品部分功能的丧失，重则可造成整个电子设备的失效。近年来，随着环境问题日趋重视电子产品无铅化已成必然［1，2］;然而，研究表明无铅焊点相对传统含铅焊点而言刚度大且较脆，使得无铅焊点对冲击载荷更加敏感。因此板级无铅焊点在冲击载荷下的可靠性研究具有重要意义。

焊点可靠性的研究通常采用实验与软件模拟仿真相结合的方法，许多研究人员已经做了大量的研究工作。大多数针对焊点疲劳寿命预测的研究都是建立在复杂的力学模型基础上，需要测得焊点应变或建立复杂的有限元模型分析得到应力等参数，很少从外部环境因素角度分析其对焊点寿命的影响。Wong［3－5］和Qiang 等［6］以断裂力学理论研究焊点寿命，Seah［7］和Caers［8］从焊点内部微损伤累积的原理研究焊点疲劳寿命，Tee［9］等把最大拉应力作为跌落碰撞下焊点失效的判断准则，用Power原理建立了一个将最大拉应力和焊点失效时跌落次数联系起来的寿命预测模型。

本文采用圆形电路板组件［10］作为跌落试件，分别测得0.34 m，0.46 m和0.78 m三种不同高度跌落时封装焊点失效数据。运用比例风险模型［11－13］以跌落高度分析其对焊点寿命的影响，并与实验数据分析得到的结果进行比较验证了模型的有效性，最后结合Miner准则［14］预测焊点损伤寿命，得到的焊点跌落寿命损伤累积模型无需建立复杂的有限元模型，无需做大量不同跌落高度下的疲劳试验，有着很好的经济性，而且以容易测得的跌落高度作为环境因素，非常便于工程应用。

1 跌落实验

文中引入贴装八个封装组件的圆形PCB板组件为跌落试件如图1。该PCB板的设计制作同JEDEC测试板，其直径为160 mm，厚度是1 mm，PCB板上焊盘类型为非焊接屏蔽界定(NSMD)，BGA封装的尺寸为11 mm×l3 mm，焊球直径为0.35 mm，球间距为0.8mm，焊料为无铅的Sn96.5Ag3.0Cu0.5。板上八个 BGA封装以PCB的中心线为轴，对称的分布在PCB上，PCB组件在跌落试验中用八个螺栓固定在基础平面上如图2，所以跌落时PCB板上的BGA封装处于同一应力应变水平，而且BGA贴装在PCB上后形成焊点的菊花链如图3所示。试验中将BGA封装形成的菊花链接入菊花链监测系统，图4是跌落碰撞下实时监控菊花链焊点动态阻值的电路原理图，外接电阻R0(1.4 Ω)与菊花链焊点串联连接到直流电源上，菊花链两端的动态阻值可以表示为:

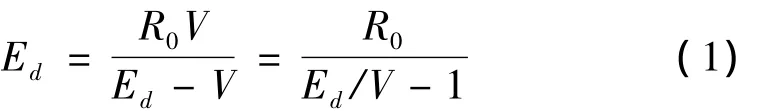
其中Ed为直流电源电压，V是菊花链两端的动态电阻Rd的动态电压，当V→Ed，Rd，→∞，电路形成开路则断定焊点失效。跌落实验中的跌落台类同于JEDEC制定的跌落测试仪器［15］。

图1 圆形PCB板试件Fig.1 The PCB board for drop test

图2 跌落固定边界条件Fig.2 The fixed boundary for the test board

图3 焊点的菊花链图Fig.3 Dynamic voltage monitoring system

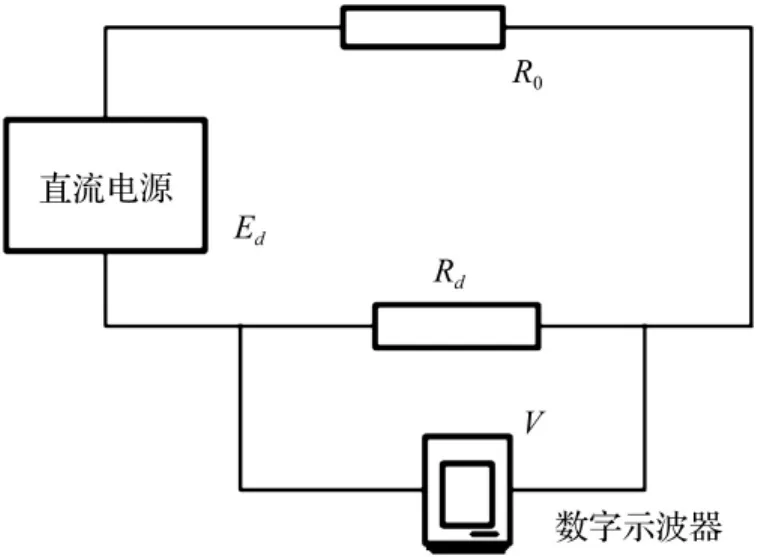
图4 菊花链检测系统Fig.4 The monitoring system of daisy chain

试验采用LMS采集器测量输入加速度的脉冲时间、脉冲形状和幅值，通过反复调整跌落高度和碰撞基面，得到试验要求的加速度脉冲幅值和脉冲时间。分别进行了三组不同脉冲幅值和脉冲时间的跌落碰撞试验:第一组，跌落高度 H=0.34 m时，产生1500 G，0.55 ms半正弦加速度脉冲;第二组，跌落高度H=0.46 m时，产生2000 G，0.5 ms半正弦加速度脉冲;第三组，跌落高度 H=0.78 m 时，产生 2700 G，0.48 ms半正弦加速度脉冲。跌落试验中采用示波器监测菊花链两端的电压，并记录每个试件上BGA封装首次失效时的跌落次数。对以上每组分别进行3个试件的跌落试验，每组可得到24个样本的跌落失效数据(如表1)做后续疲劳寿命分析。

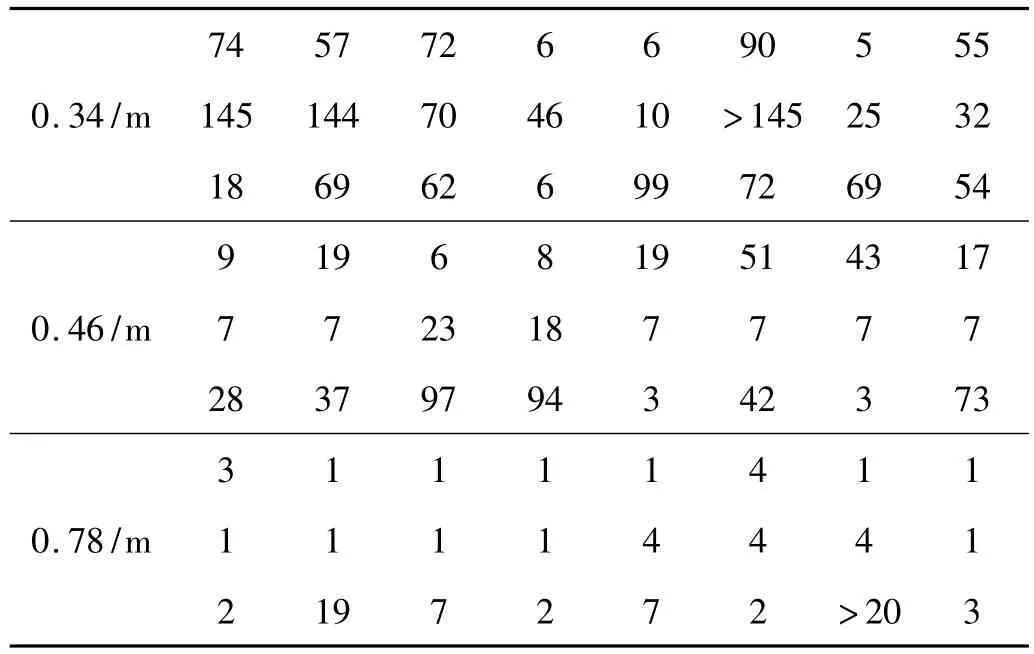
表1 跌落试验焊点失效数据Tab.1 The failure lifetines of solder joints under drop test

2 实验结果及分析

2.1 比例风险模型

比例风险模型已经被广泛运用到医学及工程领域［16－19］，分析各种因素变化对样本寿命的影响。在工程领域运用的实例表明模型能有效地估计外界因素对样本寿命产生的影响。包含时变协变量的比例风险模型由如下定义:

这里的h［t，Z(t)］为风险函数，h0(t)为基准风险函数是与时间相关的任意参数或非参数形式的函数，Z(t)为时变协变向量，β为回归系数向量。

参数比例风险模型中可以选Weibull分布，对数正态分布等作为参数基准函数，其中以Weibull分布为基准函数的应用最为普遍。本文采用Weibull分布作为比例风险模型的基准函数，其比例风险函数如下:

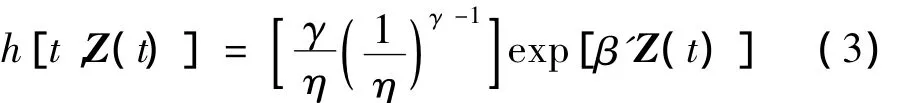
这里的γ ＞0，η ＞0为Weibull分布的形状参数和寿命参数。

一般可由极大似然估计原理得到比例风险模型中的γ，η，β等参数的估计值。假定样本由n个(包含右删失)数据组成且表示为 ［Ti，δi，，(Zi(t)，0≤t≤Ti)］，δi，为删失指数，Ti为观测失效时间则 δ=1 或为观测删失时间则δ=0，Zi(t)为协变量从0到 Ti的历史数据，则模型的极大似然函数表述如下:

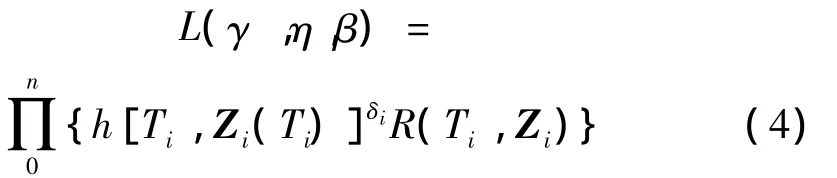
其中R(·)为样本的可靠度，可由如下积分得到:

对方程(4)两边取自然对数可得:

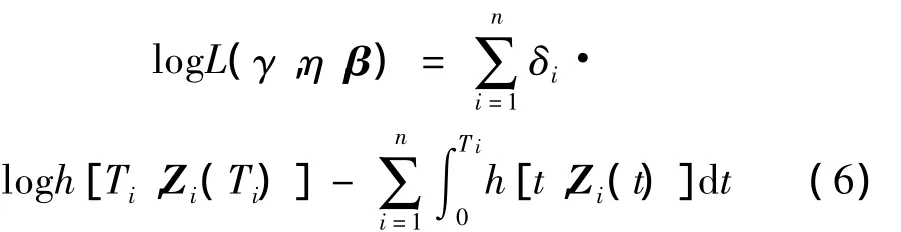
将所得样本寿命数据代入方程(6)，由最大似然估计可得各参数的估计值。

2.2 实验数据分析

本文考虑跌落高度H作为环境因素研究对焊点寿命的影响，可将H作为比例风险模型的协变量;由于每组样本的跌落高度H为定值且为非时变的，故只需一个回归系数β，则可得到考虑跌落高度H的焊点寿命的比例风险模型(PHM)为:

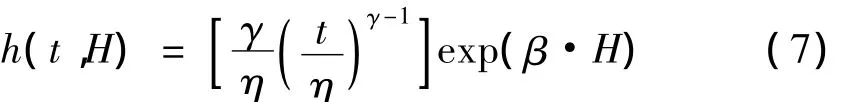
则可靠度可由积分得到:

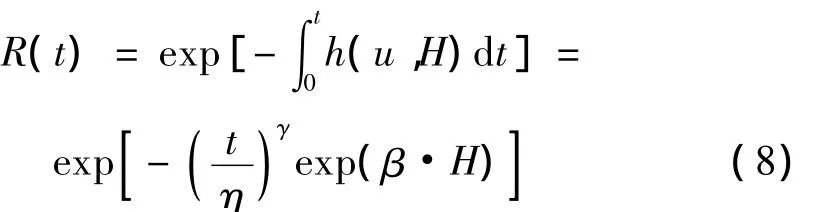
将方程(7)、(8)代入方程(6)得到模型的自然对数最大似然函数为:

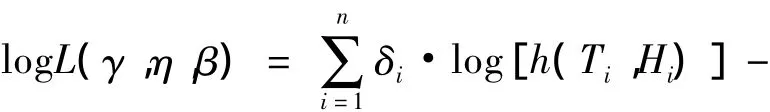
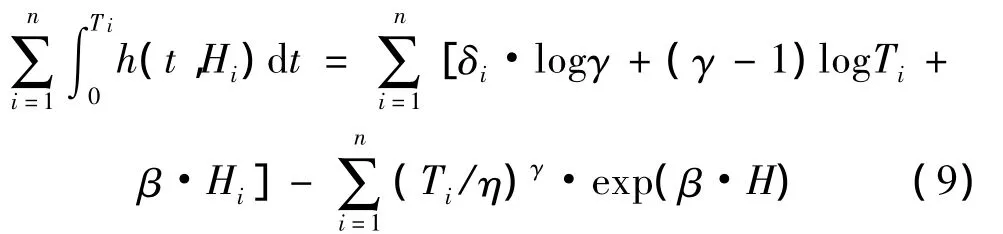
失效概率密度函数为:

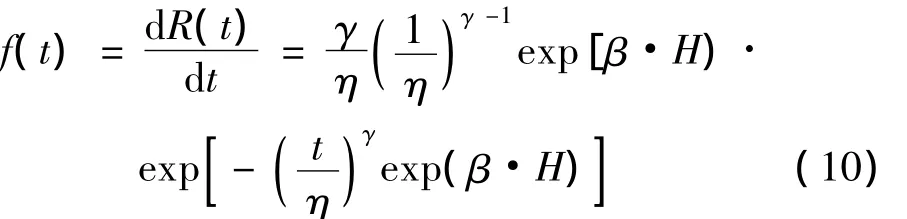
其寿命的数学期望为:

将跌落试验得到的72个样本失效数据和与其对应的跌落高度代入方程(9)，由最大似然估计原理通过求取L(γ，η，β)函数的最大值，最终得到焊点寿命PHM模型的三个参数的估计值和似然函数 L(γ，η，β)最大值如表2。

表2 PHM模型各参数γ，η，β的估计值与似然函数 L(γ，η，β)最大值Tab.2 The estimated value of γ，η，β and maximum of L(·)

由于需要用预测得到的寿命期望(MTTF)值进行焊点寿命的后续损伤累积分析，所以PHM模型估计得到的MTTF值的误差大小是评估模型的重要数据。用求得的PHM模型的参数估计值和每组跌落高度H代入方程(11)求得对应跌落高度下的焊点MTTF值并比较试验数据如表3，Experiment一栏表示试验数据算得每组跌落高度下焊点寿命均值，error一栏为PHM模型算得的焊点MTTF值与实验数据算得均值的误差。由表3对比数据可以看出PHM模型算得的结果误差都比较小，所以用得到的PHM模型来估计焊点MTTF值是精确的。

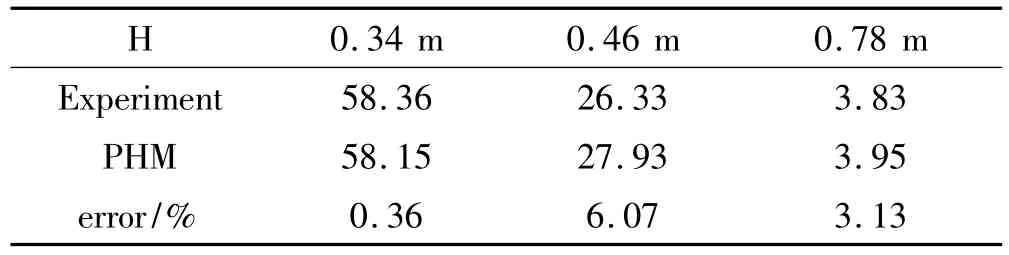
表3 PHM模型算得的焊点MTTF值及实验数据算得的均值数据Tab.3 The MTTF caleulated by PHM model and experimental data

将PHM模型各参数的估计值代入方程(10)得到随跌落高度H变化的失效概率密度函数(PDF)为:

取跌落高度 H 为 0.34 m、0.46 m、0.78 m 代入方程(12)得到对应跌落高度下焊点寿命的失效概率密度函数和实验数据得到的焊点寿命的失效概率密度函数如图5～图7。由图可知除了0.34 m跌落高度下PHM模型与试验数据在0～30、60～90寿命段有偏差外，其余都能较好地吻合。而且PHM模型估计得到的焊点寿命的失效概率密度函数在寿命的主要分布段与实验值都能够较好地吻合，特别是在高跌落高度下PHM模型能较精确地估计出焊点寿命的失效概率密度函数，说明PHM模型是有效的且能够揭示出跌落高度H与焊点寿命的失效概率密度函数隐含的数学关系。

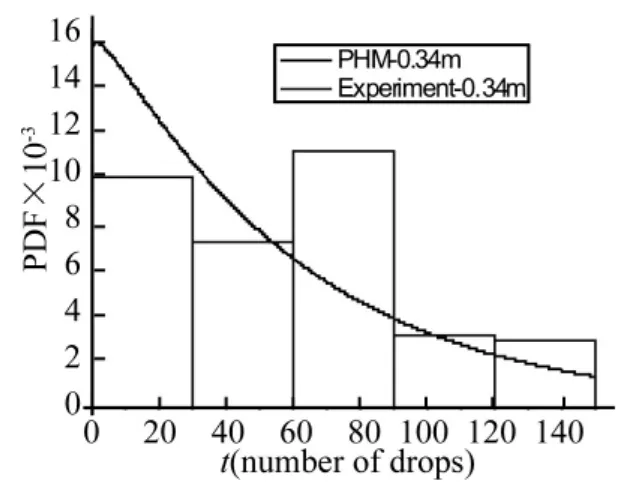
图5 0.34 m跌落高度下PHM模型与实验数据的失效概率密度函数曲线Fig.5 The failure probability density of PHM model and experimental data under drop height of 0.34 m

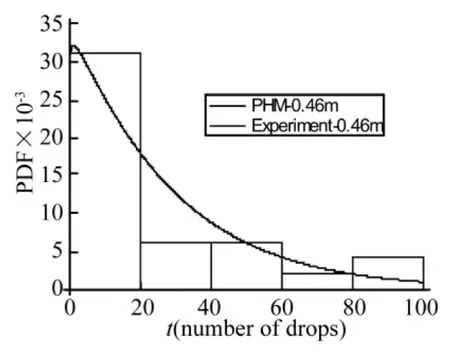
图6 0.46 m跌落高度下PHM模型与实验数据的失效概率密度函数曲线Fig.6 The failure probability density of PHM model and experimental data under drop height of 0.46 m

图7 0.78 m跌落高度下PHM模型与实验数据的失效概率密度函数曲线Fig.7 The failure probability density of PHM model and experimental data under drop height of 0.78 m

将PHM模型参数的估计值代入公式(11)得到跌落高度H变化的MTTF值别如下:

MTTF=464.426［exp(6.281·H)］0.937(13)由方程(13)得到焊点跌落MTTF值随高度变化曲线如图8，由图可知焊点MTTF值的变化率随着跌落高度递减，最终趋近于零，且图8中实验得到焊点寿命均值基本落在PHM模型估计的焊点MTTF值变化曲线上。图中由红线标出的10次跌落线可以看出，当跌落高度略大于0.6 m时焊点MTTF值都小于10次，表明无铅焊点对冲击载荷非常敏感。而且本PHM模型得到的MTTF值有着很好的经济性，只要我们得到特定跌落高度下的几组失效数据即可预测其他跌落高度下的MTTF值，而无需做大量不同跌落高度下的疲劳试验。

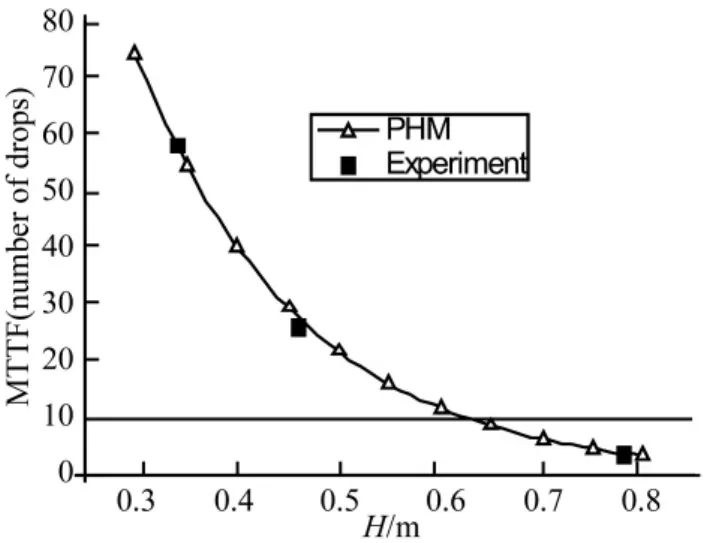
图8 跌落寿命期望值随高度变化曲线Fig.8 Lifetime curve of solder joints under drop test

Miner损伤累积原理被广泛运用于不同载荷下预测封装的疲劳寿命，如果不同载荷下累积损伤是线性的，则可得到损伤累积因子CDI为:

其中Ni为第i载荷下的样本疲劳寿命，ni为在i载荷下循环的次数，CDI取值范围从0到1.0;一般认为，0时为无损伤状态，1.0时为完全损伤状态。那么本文将Hi跌落高度下的MTTF值作为疲劳寿命代入方程(14)得到:

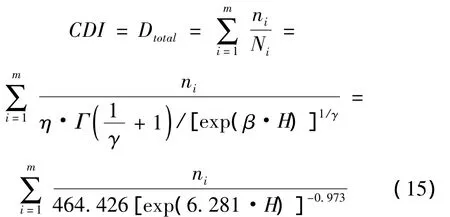
由方程(15)得到的焊点跌落寿命损伤累积模型无需建立复杂的有限元模型，跌落高度又较容易测得，而且只要我们得到特定跌落高度下的几组失效数据即可预测其他跌落高度下的MTTF值，而无需做大量不同跌落高度下的疲劳试验，节省了大量的人力和财力，非常便于工程应用。而基于损伤的可靠性分析能够被运用到以下不同的方式:工程技术人员能够计算出给定不同跌落高度及其跌落次数的累加损伤因子，得到结构损伤状况用以评估结构可靠度及其剩余寿命;设定CDI阀值作为安全设计因子，在确定载荷状况下预测结构的失效时间。

3 结论

本文以圆形电路板组件为试验试件，进行了三组不同高度的跌落试验。以跌落高度作为环境因素运用比例风险模型分析其对无铅焊点寿命的影响，用PHM模型估计的焊点MTTF值对比实验数据的均值误差较小;而且该PHM模型估计得到的焊点寿命的失效概率密度函数在寿命的主要分布段与实验值能够较好地吻合，特别是在高跌落高度下PHM模型能较精确地估计出焊点寿命的失效概率密度函数，说明此PHM模型是有效的且能够揭示不同跌落高度H与焊点寿命的失效概率密度函数隐含的数学关系。而且由焊点跌落寿命期望值随高度变化曲线可看出，当跌落高度略大于0.6 m时焊点MTTF值都小于10，表明无铅焊点对冲击载荷非常敏感。最后用估计得到的MTTF值公式结合Miner准则作为焊点跌落寿命损伤累积模型，该模型无需建立复杂的有限元模型，无需做大量不同跌落高度下的疲劳试验，有着很好的经济性，而且其参数跌落高度较容易测得，非常便于工程应用。

［1］ICER.Waste Electronic and Electrical Equipment［R］.4th draft，European Commission directive，2000，14.

［2］Challenges and efforts toward commercialization of lead free solder-Road map 2000 for commercialization of lead free solder［P］. Japan Electronic Industry Development Association，2000.

［3］Wong E H，Wong C K.Tri-layer structures subjected to combined temperature and mechanical loadings［P］.IEEE Trans Comp Packag Technol;in press.

［4］Wong E H，Lim K M，Lee N，et al.Drop impact test mechanics and physics of failure［P］.Proceedings of the fourth electronic packaging technology conference，2002:327－333.

［5］Wong E H，Seah S K W，Selvanayagam C S，et al.Recent advances in drop-impact reliability of interconnects［P］.Proceedings of the ninth EuroSIME conference，2008.

［6］Qiang Y U，Kikuchi H，Ikeda S，et al.Dynamic behaviour of electronics package and impact reliability of BGA solder joints［P］.Proceedings of the inter society conference on thermal phenomena，2002:953 －960.

［7］Seah S KW，Wong E H，Mai Y W，et al.High-speed bendtest method and failure prediction for drop impact reliability［P］.Proceedings of the 56th electronic components and technology conference，2006，1003 －1008.

［8］Caers J F J M，Seah S K W，Wong E H，et al.A study of crack propagation in Pb-free solder joints under drop impact［P］. Proceedings ofthe 58th electronic component＆technology conference，2008，1166 －1172.

［9］Tee T Y，Ng H S，Lim C T，et al.Board level drop test and simulation ofTGBGA packages for telecommunication applications［P］. Proceedings ofthe 53rd electronic component technology conference，2003，121 －129.

［10］Liu Fang，Meng Guang，Zhao Mei，et al.Board Level Drop Test Analysis Based on Modal Test and Simulation［J］.Journal of Electronic Packaging.JUNE，2008，130:021007.

［11］Chevalier R，Garnero M A，Jardine A K S，et al.Optimizing CM data from EDF main rotating equipment using proportional hazard model［P］.Surveillance 5 Conference.France，11 －13 October，2004.

［12］Danielyan S A，Zharinov G M，Osipova T T.Application of the principal components method and the proportional hazards regression model to analysis of survival data［J］.Biometrical，1986，28:73 －79.

［13］Gao Y.Application of DPCA to oil data PH model building and comparison of optimal CBM policies［R］.MSC thesis，2003，University of Toronto:Canada.

［14］Miner M A.Cumulative fatigue damage［M］.J Appl Mech，1945，12:A159 －164.

［15］JEDEC Standard JESD22 － B111，Board level drop test method ofcomponentsforhandheld electronic products［S］，2003.

［16］Jardine A K S，Joseph T，Banjevic D.Optimizing conditionbased maintenance decisions forequipmentsubjectto vibration monitoring［J］.Journal of Quality in Maintenance Engineering，1999，5:192 －202.

［17］Lin D， Banjevic D， Jardine A K S. Using principal components in a proportional hazards model with applications in condition-based maintenance［J］，Journal of Operational Research Society，2006，57:910 －919.

［18］Makis V，Jardine A K S.Optimal replacement in the proportional hazards model［J］.INFOR，1992，30:172 －183.

［19］Banjevic D，Jardine A K S，Makis V，et al.A control-limit policy and software for condition-based maintenance optimization［J］.INFOR，2001，39:32 －50.