预应力CFRP布加固损伤RC梁的动力特性研究

艾 军，单 岗，王侠伟，钱 江，杨 杰，陆耀清，徐春林

(1.南京航空航天大学 土木工程系，南京 210016;2.浙江顺畅高等级公路养护有限公司，杭州 310051)

纤维增强复合材料(Fiber Reinforced Polymer/Plastic，简称FRP)是由纤维材料与基体材料按一定比例混合并经过一定工艺复合形成的高性能新型材料。FRP以其高强、轻质、耐腐蚀等优点，开始在土木工程中得到应用，并受到工程界的广泛关注［1，2］。近些年来，预应力CFRP布加固方法逐渐成为研究热点。但是综合国内外研究现状，针对预应力CFRP布加固钢筋混凝土简支梁桥动力性能的研究较少，国内还未见有相关的报道。

本文拟通过理论与试验相结合的办法，研究预应力CFRP布加固钢筋混凝土简支梁桥的动力特性，分析预张力与被加固损伤梁固有频率之间的定量关系，以期为预应力CFRP布加固钢筋混凝土简支梁桥的加固设计提供一定的参考，同时也为预应力加固钢筋混凝土简支梁桥的检测提供一定的依据。

1 理论分析

对于预应力CFRP布加固钢筋混凝土简支梁桥，由于CFRP布被张拉后，具有一定的抗弯刚度。因此研究预应力CFRP布加固RC梁的动力特性，不能忽略预应力CFRP布的刚度影响，需要将两者综合考虑［3］。建立预应力CFRP布加固完好梁计算模型，如图1所示。

根据简支梁振动的基本理论，可推导其振动微分方程为:

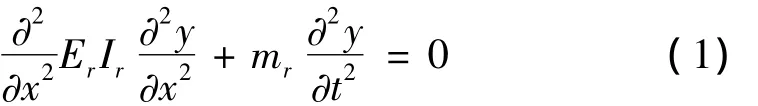
式中:ErIr为预应力加固梁总体抗弯刚度，ErIr=ECIC+ESIS;mr为预应力加固梁的总的单位长度质量，mr=ρCAC+ρSAS;ESIS为预应力CFRP布的抗弯刚度;ρSAS为预应力CFRP布单位长度的质量。

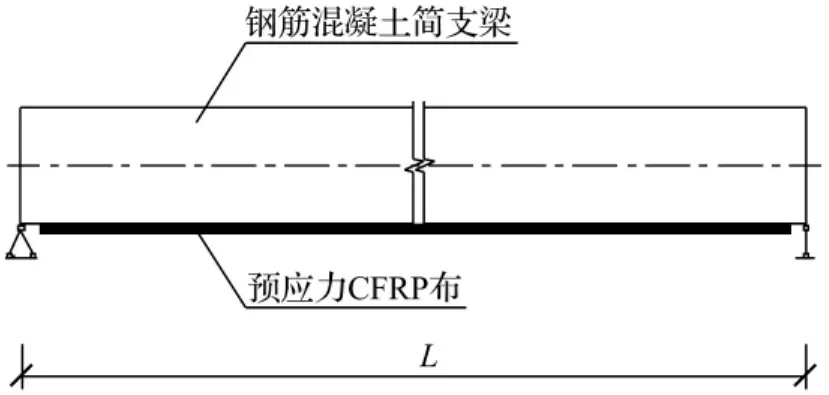
图1 理论计算模型Fig.1 Theoretical calculation model

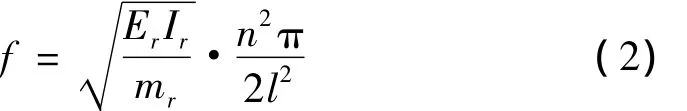
由于CFRP布的密度相对于混凝土来说很小，其质量可以忽略不计。因此求解加固梁的频率，只要求得加固梁总抗弯刚度ErIr即可，由于ECIC已知，关键是求出ESIS。

CFRP布由于被施加了预应力，使得其处于拉紧状态。同时CFRP布的宽度与长度相比很小，可将其近似为梁，计算模型如图2所示。其振动微分方程为:

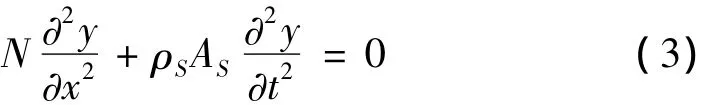
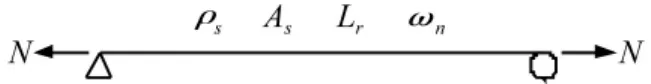
图2 预应力CFRP布计算模型Fig.2 Calculation model of prestressed CFRP sheets

图3 CFRP布等效计算模型Fig.3 Equivalent calculation model of CFRP sheets

对于式(3)，通过分离变量可以求得预应力CFRP布的频率为:

同时将预应力CFRP布的计算模型进行等效变换(计算模型如图3所示)，将其等效为具有一定抗弯刚度的普通CFRP梁，根据简支梁的振动基本理论，可以得到等效预应力CFRP梁的自振频率为:

对于式(4)与式(5)，两者应等价，进行简化后可以得到:

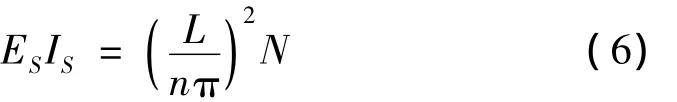
将式(6)代入式(2)，进行分析和化简，最后得到预应力CFRP布加固完好梁的自振频率计算公式如(7)所示:

其中:

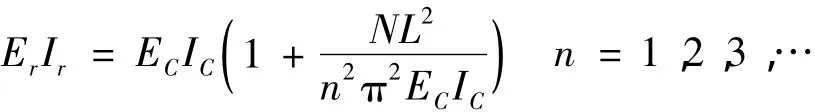
对于式(7)，未考虑混凝土压实所带来的影响;同时在计算预应力CFRP布的刚度时，将其等效为具有一定抗弯刚度的CFRP梁，故利用式(7)来计算不同预张力下完好梁的固有频率，会存在一定的误差。

因此，考虑上述两因素，引入频率影响系数λ对式(7)进行修正，修正后的结果如式(8)所示。

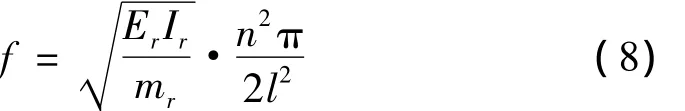
其中:

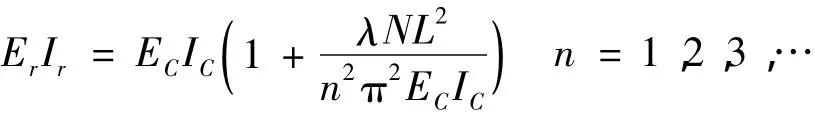
损伤梁相对于完好梁，最主要的变化就是刚度折减，引入刚度折减系数β。因此损伤梁的抗弯刚度为ErIr=βECIC，则预应力CFRP布加固钢筋混凝土损伤梁的总抗弯刚度为:

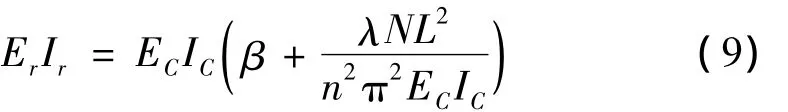
以预应力CFRP布加固完好梁的理论分析为基础，引入刚度折减系数β，则预应力CFRP布加固钢筋混凝土损伤梁的自振频率计算公式如式(10)所示:

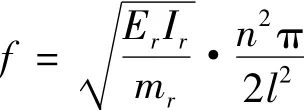
其中:

2 动力特性试验

2.1 试验简介

本次试验以一根钢筋混凝土梁为对象，其截面尺寸为150 mm×250 mm×4200 mm，计算跨径为3900 mm。架立筋为 2φ8，主筋为 2φ14，箍筋为 φ8@200，钢筋保护层厚度为25 mm。截面配筋如图4所示。

试验首先进行预应力加固完好梁的动力特性试验，而后将完好梁进行预裂，使梁体产生一定的损伤，最后进行预应力加固损伤梁的动力特性试验。试验仪器设备主要有:DH5935动态数据采集分析系统、C-AKZ型号的加速度传感器、力锤、YE2538程控静态应变仪、裂缝观测仪等。

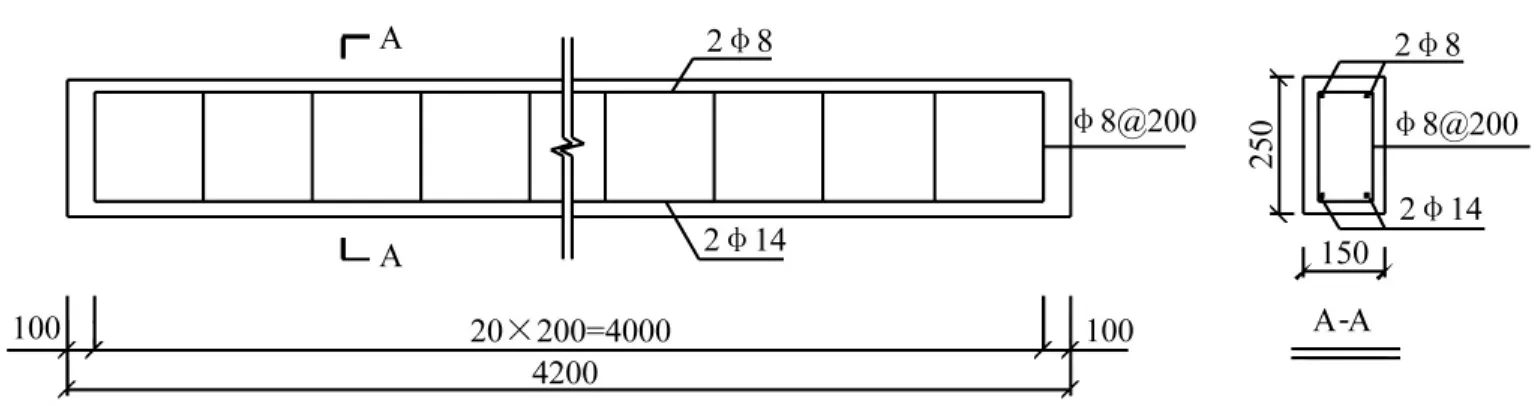
图4 试验梁截面配筋图(单位:mm)Fig.4 Reinforcement drawing of test beam

图5 锚固端实图Fig.5 Graph of anchor end

图6 试验梁实图Fig.6 Graph of test beam

图7 张拉装置实图Fig.7 Graph of straining device

图8 预应力施加示意图Fig.8 Schematic diagram of applying prestress

2.2 预应力CFRP布加固试验梁

2.2.1 锚固端处理

在完成准备工作后，进行锚固端处理。先用螺杆把上下两块钢垫板固定，在垫板与混凝土接触界面刷上胶体，再用螺帽固定。待胶凝固达到一定强度后，取一小段表面刷过胶的光圆钢筋，将CFRP布刷上胶体，绕过钢筋后，用钢压板压紧，旋紧螺帽固定，锚固端如图5所示。最后完成锚固后试验梁如图6所示。

2.2.2 预应力施加

预应力的施加主要依靠拧紧螺栓和螺帽的过程中逐渐缩短CFRP布的纵向长度而施加预应力，张拉过程中，CFRP布任何横截面均匀受力，不会产生应力集中，最大程度克服了纤维束分别受力、先后断裂的缺陷，CFRP布张拉装置及预应力施加原理如图 7、8所示。

2.3 试验梁的振动试验及实测频率

本次试验采用锤击法，利用东华DH5935动态数据采集分析系统对试验梁的振动加速度响应信号进行了测量。试验共有五个加速度传感器，在梁表面分别布置在梁的1/8跨，1/6跨，2/6跨，4/6跨，5/6跨，其中1#～5#为力锤敲击位置，具体布置情况如图9所示。

具体试验过程如下:将CFRP布张拉至相应预张力，待CFRP布应变读数稳定后，进行三种不同激振位置的振动试验，间隔击打10次，时间间隔一要保证数据采集顺利进行，二要保证上一次击打引起的振动衰减完毕。完成该预张力下试验后，利用扳手将CFRP布张拉至下一预张力，完成相应振动试验［4］。

控制预张力为 4.8、7.2、9.6、12、14.4、16.8、19.2(单位kN)，对测得加速度响应信号进行傅里叶变换(如图10～图13所示)，得到不同预张力作用下完好梁的第一阶固有频率结果如表1所示。

控制预张力为 4.8、7.2、9.6、12、14.4、16.8、19.2(单位kN)，对测得加速度响应信号进行傅里叶变换(如图14～图17所示)，得到不同预张力作用下损伤梁的第一阶固有频率结果如表2所示。

表1 实测不同预张力下完好梁第一阶固有频率(单位:Hz)Tab.1 The primary frequency value of good beam under different pretension

图9 测试传感器布置及锤击位置示意图(单位:mm)Fig.9 Arrangement of test sensor and hammering position

表2 实测不同预张力下损伤梁第一阶固有频率(单位:Hz)Tab.2 The primary frequency value of damage beam under different pretension

3 基于ANSYS钢筋混凝土损伤梁的模型修正

本章利用ANSYS软件，采用整体式建模方法，选用SOLID45单元来模拟钢筋混凝土，建立钢筋混凝土完好梁的三维有限元模型［5］。

根据式(8)，由于未施加预应力，则N=0，故完好梁各阶固有频率理论解的计算公式如下:

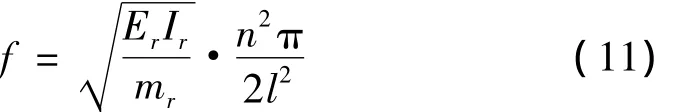
其中:

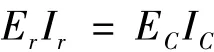
通过对模型进行模态分析，得到前四阶固有频率值，而后与理论公式的计算值进行对比分析，选取基频作为对比值，ANSYS计算的基频与理论计算结果吻合较好，相对误差仅为0.01%。

图10 完好梁在0 kN作用下频域分析曲线Fig.10 Frequency Domain analysis curve of good beam under 0 kN

图11 完好梁在7.2 kN作用下频域分析曲线Fig.11 Frequency Domain analysis curve of good beam under 7.2 kN

图12 完好梁在12 kN作用下频域分析曲线Fig.12 Frequency Domain analysis curve of good beam under 12 kN

图13 完好梁在16.8 kN作用下频域分析曲线Fig.13 Frequency Domain analysis curve of good beam under 16.8 kN

图14 损伤梁在0 kN作用下频域分析曲线Fig.14 Frequency Domain analysis curve of damage beam under 0 kN

图15 损伤梁在7.2 kN作用下频域分析曲线Fig.15 Frequency Domain analysis curve of damage beam under 7.2 kN

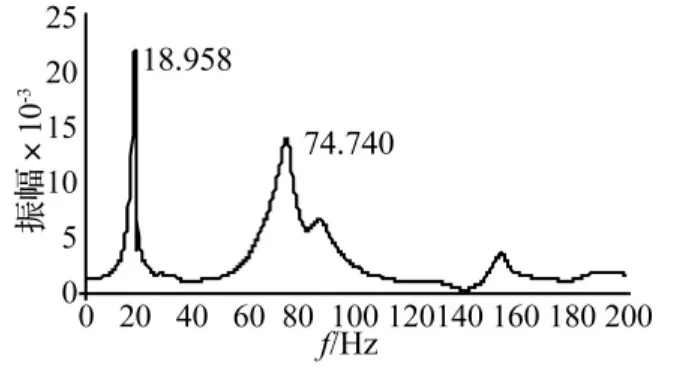
图16 损伤梁在12 kN作用下频域分析曲线Fig.16 Frequency Domain analysis curve of damage beam under 12 kN

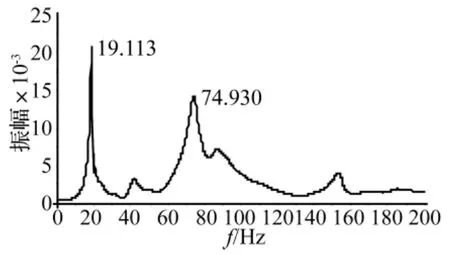
图17 损伤梁在16.8 kN作用下频域分析曲线Fig.17 Frequency Domain analysis curve of damage beam under 16.8 kN

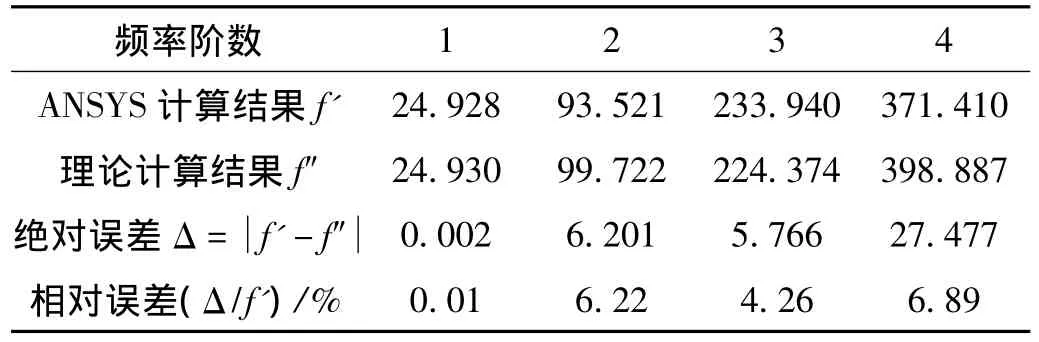
表3 ANSYS计算结果与理论求解对比分析(单位:Hz)Tab.3 Comparative analysis between results of ANSYS and theoretical calculation

由于混凝土刚度对动力特征影响较大，并且自振频率随混凝土刚度的减小而减小。为了使损伤梁的有限元模型和存在裂缝的实际模型更接近，引入刚度折减系数β。根据损伤梁的动力测试结果，以完好梁的有限元模型为基础，利用ANSYS的优化设计功能，进行损伤梁的模型修正。根据三次的优化结果，最后得到当β=0.55999时，有限元模型与实际损伤梁模型误差最小，仅为0.0085%。

4 试验值与理论值比较分析

4.1 一阶频率的线性拟合

由于本试验预张力变化范围为4.8 kN～19.2 kN。当预张力为19.2 kN时，经过计算，并未起到完全的卸荷作用，因此本试验所施加的预张力属于低预应力［6］。

分析式(8)，对于一阶频率，可以得到如下关系:

其中:

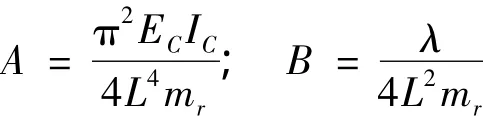
由式(12)可知，f2与N成线性关系，利用Origin软件，对试验结果进行线性拟合，结果如图18所示。

图18 完好梁的一阶频率线性拟合Fig.18 The primary frequency linear fitting of good beam

根据分析结果可知，拟合直线为:f2=617.318+1.101·N。线性拟合的相关系数为0.99135，说明拟合效果良好。

最后得到预应力CFRP布加固RC梁，预张力与频率之间的关系如式(13)所示。

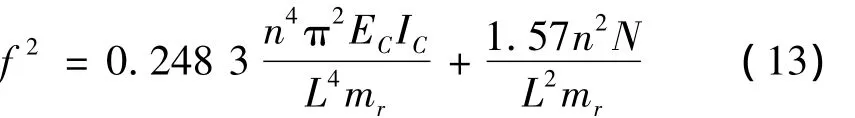
4.2 损伤梁一阶频率的试验值与理论值对比分析

对于式(13)，考虑刚度折减系数 β=0.55999，可以得到预应力CFRP布加固损伤梁预张力与频率之间的关系，如式(14)所示。

对于一阶频率与预张力之间的关系如式(15)所示。

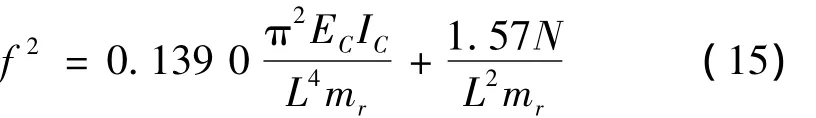
将预应力CFRP布加固损伤梁的一阶频率的试验值与理论值进行对比，具体如图19所示。

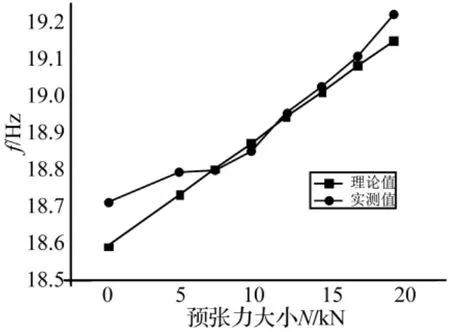
图19 损伤梁一阶频率试验值与理论值的对比Fig.19 Comparison of damage beam between test value and theoretical value

根据图19可知，当预张力N为7.2 kN和9.6 kN时，损伤梁的一阶频率的理论值大于试验值，当预张力继续增大的时候，一阶频率的试验值大于理论值，同时，随着预张力的增大，试验值的增幅也在不断地增大。经过分析认为，随着预张力的不断增加，损伤梁的混凝土被压实，同时内部的裂缝逐渐地闭合，使得损伤梁的刚度得到了提高，频率相应地增大，而且作用的预张力越大，损伤梁刚度的提高也越大，使得实测一阶频率的增幅也不断地增大。

通过分析认为，在低预应力范围内，利用式(15)所计算得到的理论结果，能基本反映出一阶频率的试验值随预张力变化的趋势。证明了利用有限元计算得到刚度折减系数方法的可行性和式(14)对计算加固损伤梁一阶频率的适用性。

5 结论

本文通过理论推导，同时考虑了相关因素影响，引入频率影响系数及刚度折减系数，得到了预张力与损伤梁频率之间的定量关系。利用完好梁一阶频率的试验数据对理论公式进行线性拟合，得到了相关的拟合系数及损伤梁频率的计算公式，最后将试验值与理论值进行比较，发现在低预应力作用下，理论计算结果能基本反映出加固损伤梁一阶频率的试验值随预张力变化的趋势，试验值与理论值吻合较好。

本文得到的预张力与被加固损伤梁固有频率之间的定量关系，可以为预应力CFRP布加固钢筋混凝土简支梁桥的加固设计提供一定的参考，同时也为预应力损失的检测提供一定的依据。

［1］田安国.预应力FRP加固混凝土受弯构件试验及设计理论研究［D］.南京:东南大学，2006.

［2］吴 刚.FRP加固钢筋混凝土结构的试验研究与理论分析［D］.南京:东南大学，2002.

［3］Jeong-Tae K，Yeon-Sun R，Chung-Bang Y.Vibration-based method to detect prestress-loss in beam-type bridges［J］.Proceedings of the SPIE-The International Society for Optical Engineering，2003，5058:559－568.

［4］胡海岩.机械振动基础［M］.北京:北京航空航天大学出版社，2005.

［5］刘相新，孟宪颐.ANSYS基础与应用教程［M］.北京:科学出版社，2006:3－8.

［6］张学富，姚国文.桥涵维护与加固技术［M］.北京:人民交通出版社，2007.