大型冷却塔双塔干扰的风洞试验研究

沈国辉，余关鹏，孙炳楠，楼文娟，李庆祥，杨仕超

(1.浙江大学 土木工程学系，杭州 310058;2.广东省建筑科学研究院，广州 510500)

大型双曲自然通风冷却塔由于体型巨大，壁厚极薄，风荷载是主要的控制荷载。1965年英国渡桥电站冷却塔群中，处于下风向的三座塔在五年一遇的大风中发生倒塌，引起人们对冷却塔干扰效应的重视。对于在实际工程中较为常见的双塔干扰问题，已有一些研究人员采用风洞试验和数值模拟等手段进行研究。

在风洞试验方面，顾志福等［1］分析不同排列时冷却塔的平均和脉动风压;Orlando等［2］研究三种排列情况下典型风压的干扰系数;张彬乾等［3］分析冷却塔双塔干扰时平均风压的变化规律;赵林等［4］根据某电厂实际布局采用等效风荷载比例系数来量化干扰。在数值模拟方面，刘若斐等［5］采用CFD方法分析受干扰冷却塔的压力系数;沈国辉等［6］针对不同的塔间距和风向角，获得冷却塔阻力系数的变化规律。以上成果主要分析了双塔情况下冷却塔表面风压的变化，对冷却塔整体风荷载作用如阻力、升力、底部剪力等的系统研究尚缺乏。

本文采用风洞试验的同步测量技术获得冷却塔外表面的风压，通过增加模型表面粗糙度的方法以补偿模型试验的雷诺数效应，应用本征正交分解法(POD)［7，8］进行风压数据点的插值和加密，最后通过对阻力系数、升力系数、底部剪力系数等分析进行双塔干扰效应的研究。

1 风洞试验简介

1.1 冷却塔模型

冷却塔高150 m，塔顶半径为 36 m，底部半径为 60 m，颈部高112.5 m，颈部半径为 33.27 m，塔底由48对均匀分布的人字柱支撑。模型按 1∶300缩尺比制作，冷却塔的几何尺寸和测点布置如图1所示。共布置5层外压测点，编号为A ～E，分别对应于 140 m、110 m、80 m、50 m、20 m高度，每层沿环向均匀布置36个测点，共布置180个测点。

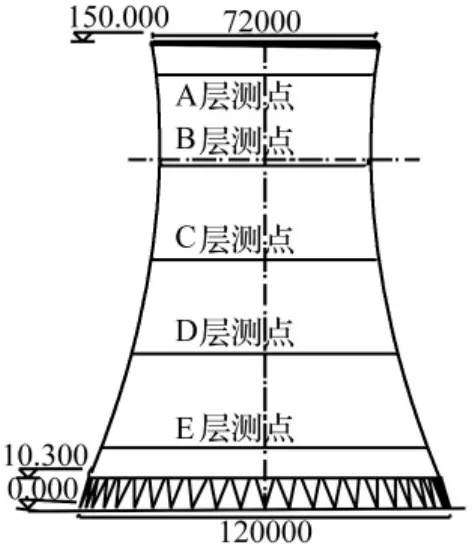
图1 冷却塔的几何尺寸和测点布置Fig.1 Schematic diagram of cooling tower and measuring taps

1.2 风洞和风场模拟

风洞试验在广东省建筑科学研究院的CGB－1风洞中进行，风洞试验段长10 m，宽3 m，高2 m。三角尖劈和地面粗糙元置于来流前部，用以模拟B类地貌的大气边界层，试验照片如图2所示。风压测量采用美国Scanivalve公司的DSM3200电子扫描阀，使用三组模块，可进行192个测点的同步测压。

图2 冷却塔的风洞试验照片Fig.2 Cooling tower picture in wind tunnel

根据结构荷载规范［9］要求，B类地貌大气边界层的平均风速V剖面按指数规律变化。对于湍流度Iu剖面，我国规范没有要求，参考日本AIJ规范［10］有:

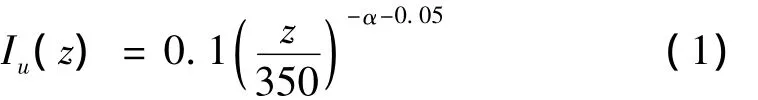
式中z为高度，α为地面粗糙度指数，对于B类地貌取0.16。风洞模拟的风速和湍流度剖面如图3所示，图中平均风速剖面以高度为H的塔顶处风速VH进行无量纲处理，可见风洞中很好地模拟了B类地貌的边界层。

1.3 数据处理

风压系数Cp以塔顶高度H的速度压作为参考:

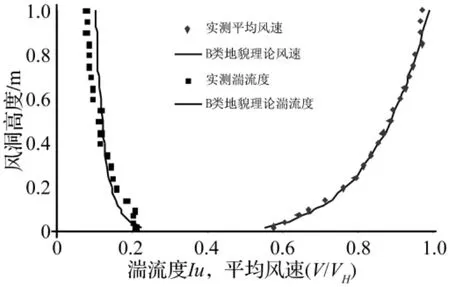
图3 风洞模拟的平均风速和湍流度剖面Fig.3 Simulated profiles of mean velocity and turbulence intensity

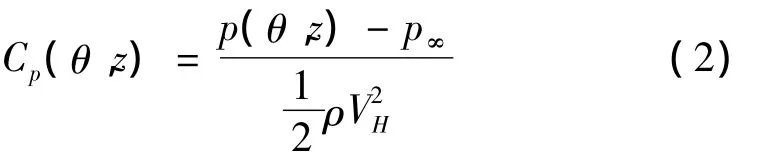
式中:p(θ，z)是测点的压力值，p∞为参考点的静压值，θ为圆周角，ρ为空气密度。

冷却塔的截面为圆形，可以计算该截面顺风向的阻力和横风向的升力。假设沿截面均匀分布N个风压测点，阻力系数CD和升力系数CL的计算公式为:

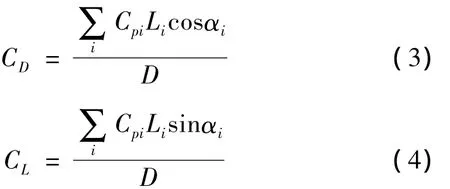
式中:Li为测点所占的长度，αi为测点的法向与来流风向的夹角，D为截面直径。

将冷却塔表面的风荷载合成为作用于底部的顺风向剪力Q，剪力系数CQ的计算公式为:

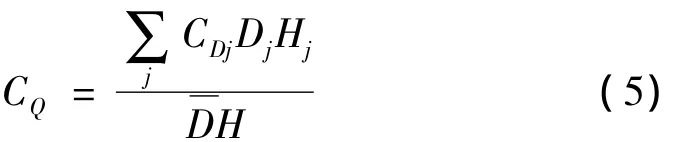
式中Dj为冷却塔j层的直径，Hj为j层风压点所占的高度为冷却塔的平均直径。

2 模型表面粗糙度的选取

风洞试验的雷诺数与实际往往相差两个数量级，对于圆形截面的冷却塔，雷诺数的影响非常大，因此需要采用一定的方法来补偿模型试验的雷诺数不匹配。Farell［11］和 Sun 等［12］均成功采用提高模型表面粗糙度的方法来补偿模型试验的雷诺数效应，本次试验采用在模型表面粘贴胶带的方法来提高表面的粗糙度。

在模型外表面沿子午线方向均匀粘贴胶带，胶带厚度分别为 0.1 mm、0.2 mm、0.4 mm、0.6 mm，胶带条数为36条。图4给出厚度为0.4 mm时的B层测点的体型系数分布，并将以前的现场实测、相近试验条件的模型试验结果和规范数据绘于图中进行比较。图中所有的数据均换算为结构荷载规范［9］意义上的体型系数，且各数据所在测层均位于冷却塔的喉部及喉部附近。由图可知，厚度为0.4 mm的表面粗糙度比较合理，后面的单塔和双塔试验均采用该粗糙度。

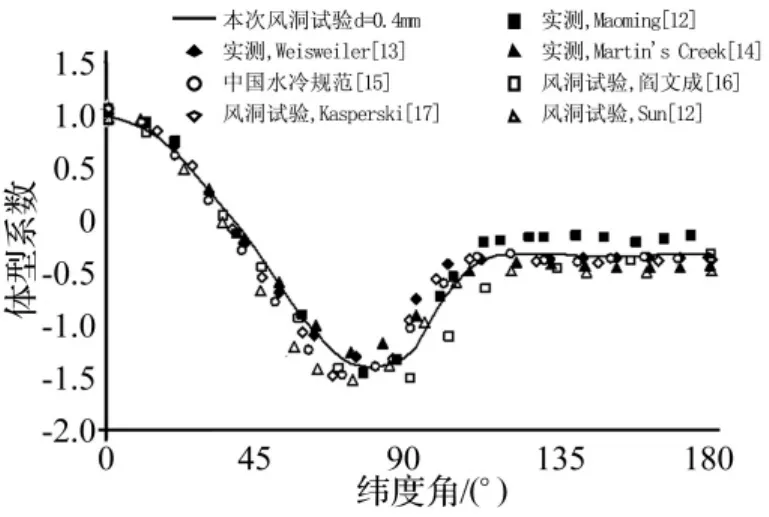
图4 本次试验与规范、实测及以往试验值的比较Fig.4 Data comparisons between present test with Code，full-scale tests and others’wind tunnel tests

3 本征正交分解法

由公式(5)可知，在计算风荷载作用下冷却塔的底部剪力时，需要的风压数据点越多越好。由于风洞试验中同步测压的测点数目有限，本次试验为180个测点，因此需要进行风压数据点的插值和加密。本征正交分解法已经成功用于高层建筑和屋盖结构风压场的插值和加密［7，18，19］，因此本文采用该方法。其原理如下表述。

3.1 POD的原理

假设p(x，y，t)为随机风压函数，其中 x、y表示位置坐标，t表示时间。POD方法将其分解为:

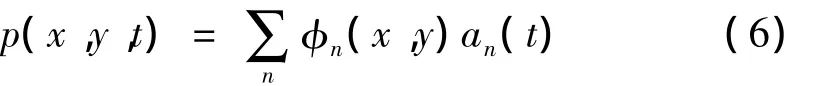
式中φn(x，y)为特征向量，an(t)为主坐标函数。POD的特征向量和特征值可以通过求解下列方程获得:

式中Rp(x，y，x'，y')为风压的协方差矩阵，λ为特征值。

3.2 单塔数据的POD分析

对单个冷却塔的数据进行POD分析，获得特征值和特征向量，归一化特征值和特征值累加如图5所示。可以发现第1阶特征值为25.4%，前19阶和40阶特征值的累计值分别为80%和90%，这个结论和某高层建筑POD分析［7］的结论非常接近。图6和图7分别给出第1阶和第2阶特征向量，可以发现第一阶POD特征向量呈对称分布，第二阶POD特征向量呈反对称分布，该分布特征和某圆柱面的POD特征向量［8］一致。

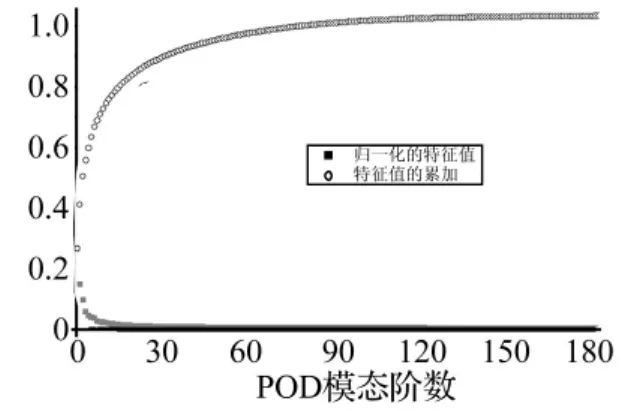
图5 单塔POD的特征值分布Fig.5 POD eigenvalues distribution of isolated tower

图6 单塔POD分析的1阶特征向量Fig.6 First POD eigenvector of isolated tower

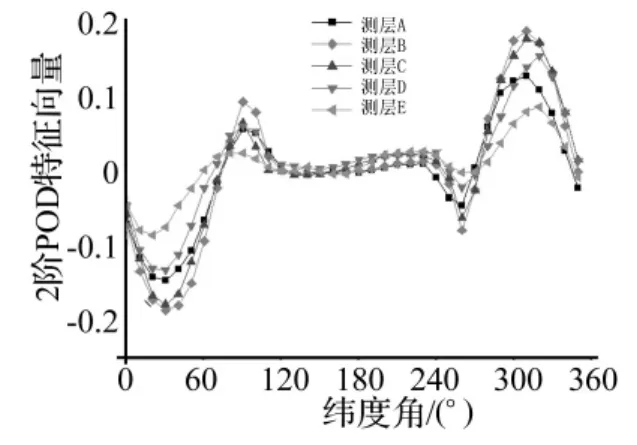
图7 单塔POD分析的2阶特征向量Fig.7 Second POD eigenvector of isolated tower

3.3 风压时程的POD插值和加密

运用POD方法进行风压系数时程的插值和加密，计算中使用全部的180阶POD模态，通过对POD特征向量的插值，可以获得未布测点处的风压时程。文献［19］进行了多种POD模态插值方法的对比，发现立方插值(cubic)具有较好的精度，因此本文采用立方插值方法，将原来5×36个风压测点时程插值成50(竖向)×72(纬向)个风压点的时程。

4 单塔的数据分析

根据POD插值加密获得的50×72个风压点的时程，可以计算得到沿高度分布的阻力系数、升力系数，以及底部剪力系数的时程。虽然就某个测点而言，其时程分布可能不符合正态分布，但对于很多个风压点叠加后的时程，其分布非常接近正态分布，图8为单塔B测层升力系数时程数据的分布，发现与正态分布吻合较好。这个结论也可用中心极限定理来说明，即当独立随机变量的个数增加时，其和的分布趋于正态。因此各响应(阻力系数、升力系数、底部剪力系数)的极大值可以采用平均值与3倍标准差之和来计算，即具有99.87%的极值保证率。

图9给出单塔情况下阻力系数CD随高度变化的平均值、标准差和极大值。可以发现平均阻力系数较大，范围为0.33～0.57，在60 m高度处最小，在塔顶最大。阻力系数的标准差沿高度几乎不变，在塔顶略大，范围为0.06～0.12，极大值的分布与平均值相似。图10给出了单塔情况下升力系数CL随高度变化的平均值、标准差和极大值。可以发现单塔的平均升力系数几乎为零，即对于圆形截面，其横风向的平均风荷载合力为零。但升力系数的标准差较大，与阻力系数的标准差相当，范围为0.08～0.12，升力系数的极大值也相当大，范围为0.24～0.35。因此，虽然单塔情况没有平均升力系数，但脉动升力系数却相当大，在设计中应引起重视。

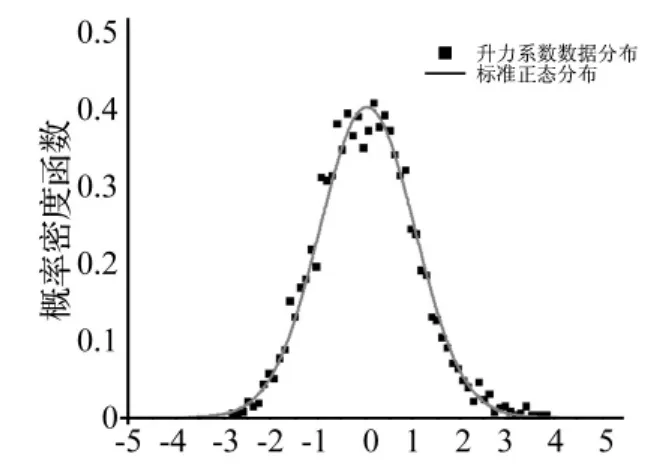
图8 B测层升力系数时程的数据分布图Fig.8 Distribution of time history of lift coefficients at measuring layer B

图9 单塔阻力系数的统计值Fig.9 Statistic values of drag coefficient of isolated tower

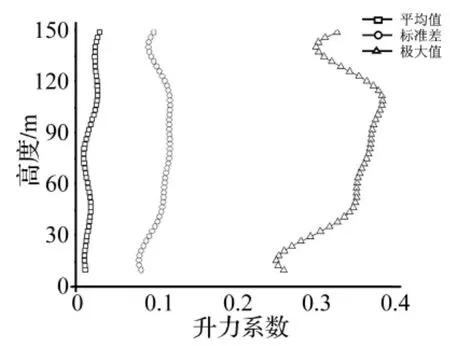
图10 单塔升力系数的统计值Fig.10 Statistic values of lift coefficient of isolated tower

5 双塔干扰的数据分析

进行双塔干扰的风洞试验，测压塔置于转盘中心，放置干扰塔，试验的平面布置如图11所示。两塔中心连线与来流风向的夹角为风向角β，0°～180°风向角每隔15°为一个工况，其中0°～30°之间加密，每隔5°为一个工况;塔间距N/D(塔中心距/塔底直径)为1.3～2.5，其中1.3 ～1.6 的变化步长为0.05，1.6 ～2.5 的步长为0.3。如下定义干扰系数IF，其中响应包括沿高度变化的阻力系数、升力系数，以及底部剪力系数。

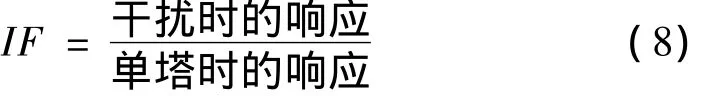
5.1 阻力的干扰效应

阻力系数CD的干扰系数主要和三个参数相关:塔间距、风向角和测层高度。工程设计中常见的塔间距为N/D=1.5，图12给出该塔间距下平均阻力系数的干扰系数，可以发现存在三种干扰情况:① 0°～75°风向角，干扰塔对测压塔产生“遮挡”作用，测压塔位于干扰塔的尾流区，干扰系数小于1;② 90°～150°风向角，干扰塔位于测压塔的侧面，产生“狭缝”效应，两塔中间的空气流动加速，部分截面的干扰系数大于1，这些截面主要位于冷却塔的底部和顶部;③ 165°～180°风向角，干扰塔位于测压塔的尾流区，处于下游的干扰塔对气流产生一定的阻挡，导致测压塔背风面风压变小，干扰系数小于1。

从图12还可以发现，0.95 H高度的干扰系数最大，图13给出该高度处各种塔间距的干扰系数。可以发现，干扰效应大于1的情况主要集中在90°～150°风向角，即狭缝效应起作用的风向角。在这些风向角下，可以发现塔间距越小，干扰系数越大，说明狭缝效应越显著。

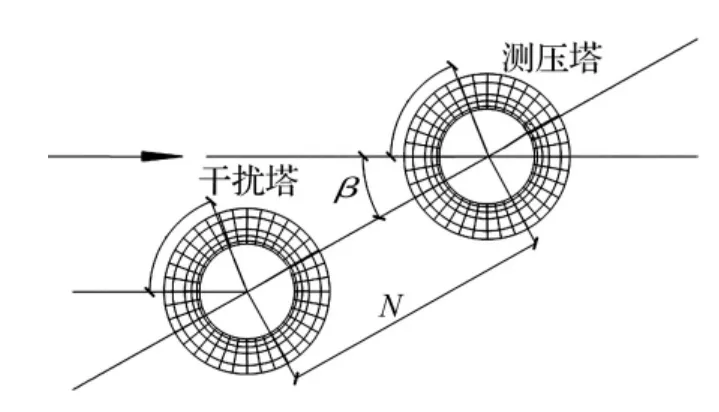
图11 双塔风洞试验的平面布置示意图Fig.11 Schematic diagram of two adjacent towers in wind tunnel test

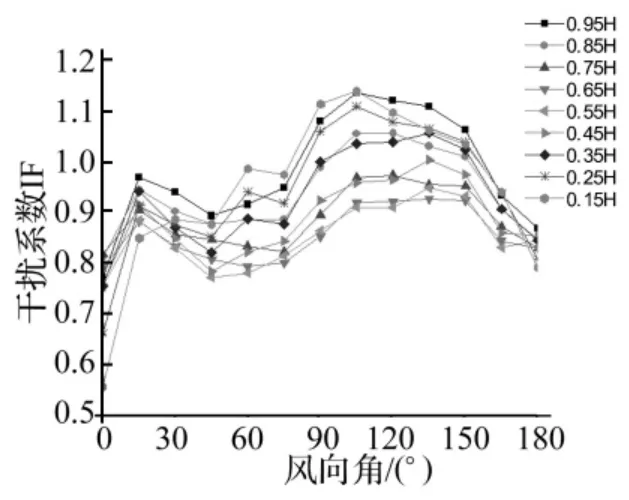
图12 N/D=1.5时平均阻力系数的干扰系数Fig.12 IF of mean drag coefficients when N/D=1.5

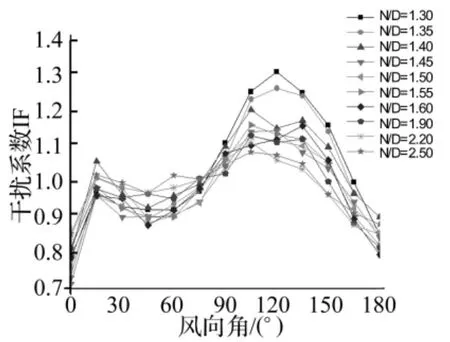
图13 0.95 H高度处平均阻力系数的干扰系数Fig.13 IF of mean drag coefficients at height of 0.95 H

以上考虑的是平均阻力系数，下面考虑脉动情况，图14给出塔间距N/D=1.5时阻力系数极大值的干扰系数，可以发现其分布与平均值的干扰系数非常相似，即也存在着三种干扰情况，唯一的区别是0°和15°风向角下部分高度的干扰系数大于1。图15给出0.95H高度处阻力系数极大值的干扰系数，可以发现其分布与平均阻力系数的干扰系数非常接近。从上面的分析可知:对于阻力的干扰效应，阻力系数的平均值和极大值对应的干扰系数几乎相同。

5.2 升力的干扰效应

由于单塔情况下平均升力系数几乎为零，因此不能计算双塔情况下的干扰系数，图16给出N/D=1.5情况下的平均升力系数。可以发现，0°和180°风向角下的平均升力系数几乎为零，即此时风场呈对称分布，不存在横风向的平均升力;平均升力系数在90°和15°附近存在极值;平均升力系数在0°～30°风向角范围内变化剧烈。本次试验在0°～30°风向角范围内进行了工况的加密，图17中给出该范围内的平均升力系数。可以发现在10°风向角时平均升力系数达到最大值，最大的数据为0.15。从图中还可知平均升力系数沿高度的分布规律:中间高度较大，两端(塔顶、塔底)较小。

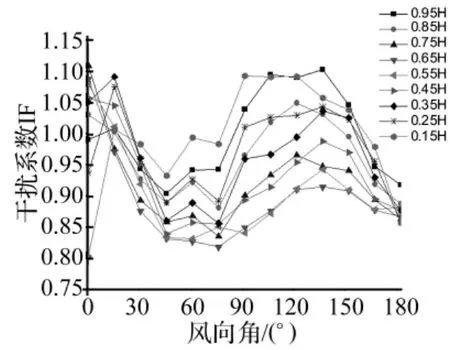
图14 N/D=1.5时阻力系数极大值的干扰系数Fig.14 IF of dynamic drag coefficients when N/D=1.5

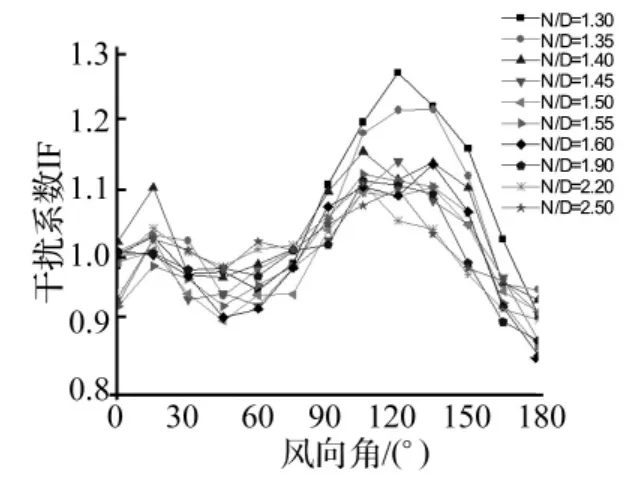
图15 0.95 H高度处阻力系数极大值的干扰系数Fig.15 IF of dynamic drag coefficients at height of 0.95 H

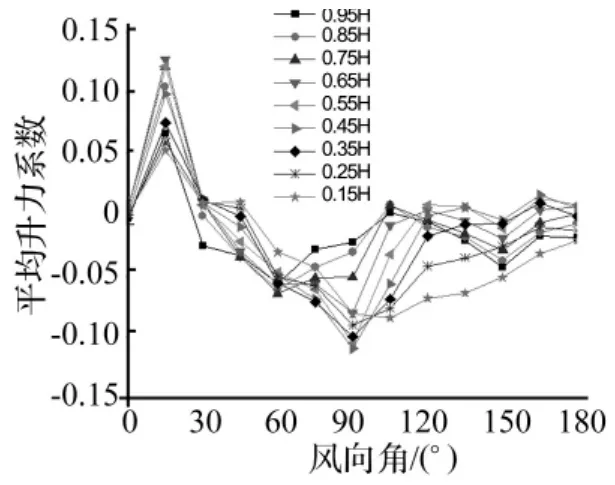
图16 N/D=1.5 时的平均升力系数Fig.16 Mean lift coefficients when N/D=1.5

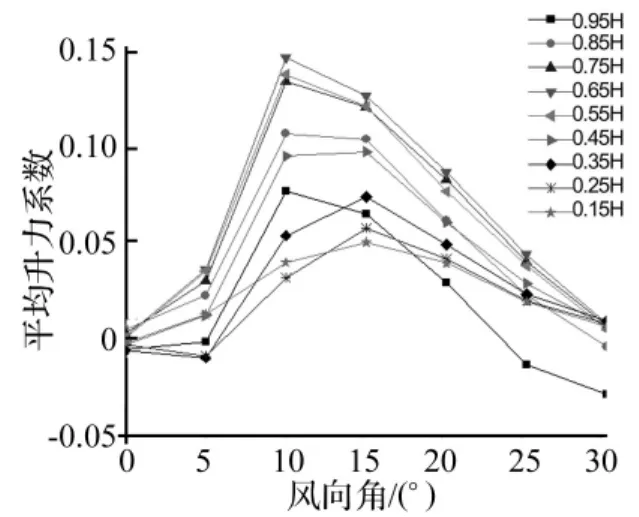
图17 N/D=1.5时的平均升力系数 ( 0°～30°风向)Fig.17 Mean lift coefficients when N/D=1.5(0°～30°)

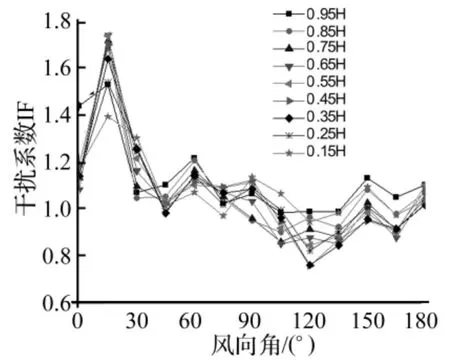
图18 N/D=1.5时升力系数极大值的干扰系数Fig.18 IF of dynamic lift coefficients when N/D=1.5

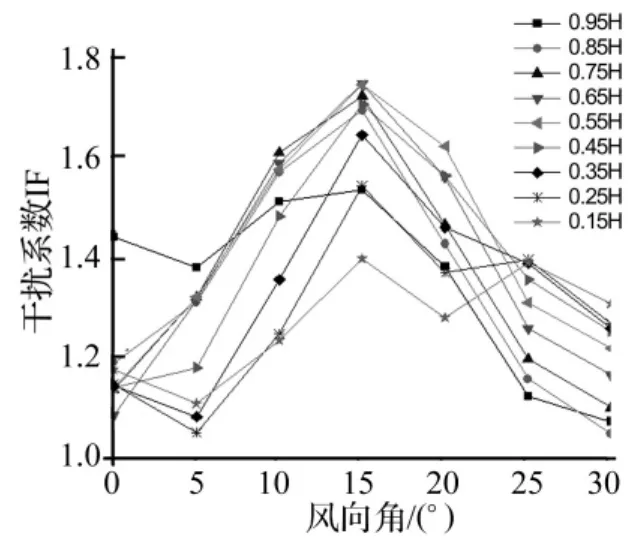
图19 N/D=1.5时升力系数极大值的干扰系数(0°～30°风向)Fig.19 IF of dynamic lift coefficients when N/D=1.5(0°～30°)

下面考虑脉动情况，图18给出N/D=1.5情况下升力系数极大值的干扰系数，可以发现大部分的干扰系数都大于1，说明双塔情况下升力系数的极大值得到了放大，最大值出现在15°风向角附近。图19给出0°～30°风向角范围加密工况的干扰系数，可以发现在15°风向角干扰系数达到最大值，最大的数据为1.75。由于单塔的升力系数极大值较大，范围为0.24～0.35，而双塔情况下的干扰系数也大，最大的数据为1.75，因而双塔情况下升力系数的极大值就非常大。而根据一般的常识，冷却塔横风向的升力系数都认为很小，而本次风洞试验的结果却表明双塔情况下升力系数的极大值非常大，因此在设计时应引起特别的重视。同时升力系数极大值的干扰系数沿高度分布规律为:中间高度较大，两端较小，这个分布规律同平均升力系数的分布。

5.3 底部剪力的干扰效应

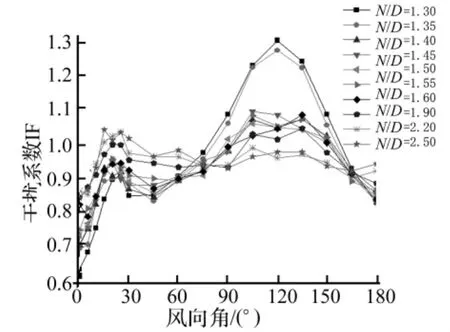
图20 顺风向底部剪力系数平均值的干扰系数Fig.20 IF of mean base shear coefficients in along-wind direction

根据公式(5)可计算得到冷却塔顺风向的底部剪力系数，底部剪力系数可以反映冷却塔受到的总体风荷载。计算得单个冷却塔的顺风向底部剪力系数，其平均值、标准差和极大值分别为 0.40、0.05 和 0.54。图20给出双塔情况下顺风向底部剪力系数平均值的干扰系数，可以发现大部分风向角下的干扰系数都小于1，除了产生狭缝效应的90°～150°风向角。同时发现在90°～150°风向角范围内，塔间距 N/D为1.3和1.35时的干扰系数特别大，最大数据为1.3。也就是说，对于塔间距N/D为1.3和1.35时，冷却塔受到的总体阻力比单塔情况大很多，因此在设计中应使塔间距大于1.35。图21给出了顺风向底部剪力系数极大值的干扰系数，发现和平均值干扰系数的结论几乎相同。

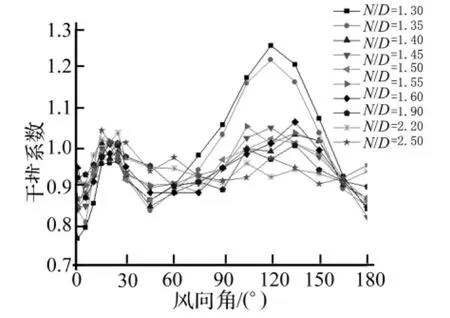
图21 顺风向底部剪力系数极大值的干扰系数Fig.21 IF of dynamic base shear coefficients in along-wind direction

6 结论

(1)提高模型表面粗糙度可补偿模型试验的雷诺数效应，通过数据的对比发现，本次试验采用36条均匀分布、厚度为0.4 mm的胶带为非常合适的表面粗糙度。

(2)单塔情况下，平均阻力系数较大，平均升力系数为零;阻力系数和升力系数的标准差数据相当;升力系数的极大值较大，须引起设计的注意。

(3)双塔情况下，平均阻力系数的干扰系数根据风向角可分成三种情况，干扰系数大于1对应于干扰塔位于测压塔的侧面情况，此时有狭缝效应产生。同时阻力系数的平均值和极大值对应的干扰系数几乎相同。

(4)双塔情况下，升力系数极大值干扰系数的大部分数据都大于1，最大数据达1.75，说明升力系数的极大值比单塔情况得到放大。而一般常识都认为冷却塔横风向的升力很小，因此在设计时应引起特别的重视。

(5)顺风向底部剪力反映冷却塔受到的总体风荷载。对于双塔情况下塔间距N/D为1.3和1.35时，底部剪力系数的干扰系数在个别风向角下会接近1.3，因此在设计中应尽量避免1.35及以下的塔间距。

［1］顾志福，孙天风，陈 强.两个相邻冷却塔风荷载的相互作用［J］.空气动力学学报，1992，10(4):519－524.

［2］Orlando M.Wind-induced interference effects on two adjacent cooling towers［J］.Engineering Structures，2001，23:979－992.

［3］张彬乾，李建英，阎文成.超大型双曲冷却塔双塔干扰的风荷载特性研究［J］.流体力学试验与测量，2003，17(特刊):93－97.

［4］赵 林，宋锦忠，高 玲，等.冷却塔刚体测压试验研究［J］.实验流体力学，2007，21(2):56－62.

［5］刘若斐，沈国辉，孙炳楠.大型冷却塔的数值模拟研究［J］.工程力学，2006，23(Sup I):177－183.

［6］沈国辉，刘若斐，孙炳楠.双塔情况下冷却塔风荷载的数值模拟［J］.浙江大学学报工学版，2007，41(6):1017－1022.

［7］Tamura Y，Suganuma S，Kikuchi H，et al.Proper orthogonal decomposition of random wind pressure field［J］.Journal of Fluids and Structures，1999，13:1069 －1095.

［8］Holmes J D.Analysis and synthesis of pressure fluctuations on bluff bodies using eigenvectors［J］.Journal of Wind Engineering and IndustrialAerodynamics， 1990， 33:219－230.

［9］建筑结构荷载规范(GB50009－2001)［S］.北京:中国建筑工业出版社，2002.

［10］AIJ Recommendations for Loads on Buildings［M］.Japan:Architectural Institute of Japan，2004.

［11］Farell C，Guven O，Maisch F.Mean wind loading on roughwalled cooling towers［J］. Journalofthe engineering Mechanics division，ASCE，1976，102(EM6):1059－1081.

［12］Sun T F，Zhou L M.Wind pressure distribution around a ribless hyperbolic cooling tower［J］. Journal of Wind Engineering and IndustrialAerodynamics， 1983， 14:181－192.

［13］Niemann H J，Propper H.Some properties of fluctuating wind pressures on a full-scale cooling tower［J］.Journal of Industrial Aerodynamics，1975/1976，1:349 －359.

［14］Steinmetz R L，Billington D P，Abel J F.Hyperbolic cooling tower dynamic response to wind［J］.Journal of the Structural Division，ASCE，1978，104(ST1):35－53.

［15］工业循环水冷却设计规范(GB/T50102－2003)［S］.北京:中国计划出版社，2003.

［16］阎文成，张彬乾，李建英.超大型双曲冷却塔风荷载特性风洞试验研究［J］.流体力学试验与测量，2003，17(特刊):85－89.

［17］Kasperski M，Niemann H J.On the correlation of dynamic wind loads and structural response of natural-draught cooling towers17［J］.Journal of Wind Engineering and Industrial Aerodynamics，1988，30:67 －75.

［18］Uematsu Y，Sone T，Yamada M，et al.Wind-induced dynamic response and its load estimation for structural frames of single-layer latticed domes with long spans［J］.Wind and Structures，2002，5(6):561 －580.

［19］李方慧，倪振华，沈世钊.POD方法在双坡屋盖风压场预测中的应用［J］.工程力学，2007，24(2):68－73.