干气密封系统角向摆动的稳定性及其振动响应

张伟政，俞树荣，丁雪兴，，韩明君，杜兆年

(1.兰州理工大学 石油化工学院，兰州 730050;2.兰州理工大学 温州泵阀工程研究院，温州 325105;3.兰州理工大学 理学院，兰州 730050)

干气密封动静环间气膜平衡间隙仅为3 μm～5 μm，显然间隙微小变化极有可能导致动静密封环间的干摩擦或泄漏量增大，因而保证气膜－密封环动态稳定性是干气密封可靠运行的关键［1］。Zhang、Miller和landers［2］建立了三自由度(1个轴向，2个角向)的微扰运动方程，并用正交分解法求得了密封环三维运动规律，在进行干气密封振动响应分析时，可将1个轴向，2个角向的三自由度的微扰运动简化为两个互相独立的微扰运动，一个只作轴向的微扰移动，另一个只沿两个正交轴作角向微扰摆动［3］。Miller、李双喜、杜兆年等［4－6］分别用步进法、有限元法、近似解析法求解了轴向微扰下气膜动态特性参数，分析了其轴向稳定性。丁雪兴［7］利用近似解析法求得了角向涡动气膜刚度的解析式，Etsion［8，9］通过试验和理论计算获得了在角向微扰下摆动自振频率约等于动环角速度之半;刘雨川、徐万孚［10，11］按照小扰动线性化的分布参数法，联立气膜微扰雷诺方程和浮环运动方程，对角向摆动自振稳定性界限进行了数值分析。但以上均未揭示干气密封系统角向摆动失稳的内在因素，即密封系统稳定性与螺旋槽几何参数的关系。本文建立了角向摆动惯量的稳定性条件，通过龙格－库塔法求得了临界转动惯量与槽深比、螺旋角的三维关系曲面图，进而分析了系统稳定时的槽深比、螺旋角范围;并应用微扰法和龙格－库塔法求解了角向摆动的二维振动方程，研究了最佳稳定点和失稳临界点振动响应，发现了具有非线性动力学特征的混沌现象，为动态优化提供了理论基础。

1 密封系统角向摆动的稳定性条件

干气密封结构主要由加载弹簧(波纹管)、O形圈、静环以及动环组成(图1)。当压力达到一定数值时，具有挠性支承的静环将从动环表面被推开，这样密封面之间保持一层极薄的气膜(厚度3 μm～5 μm)。

端面流体气膜密封不转浮环(静环)端面处，在单向任意干扰下绕其两正交轴(x，y)，作角向摆动α*，β*见图2，其摆动惯量为Jx=Jy=J。

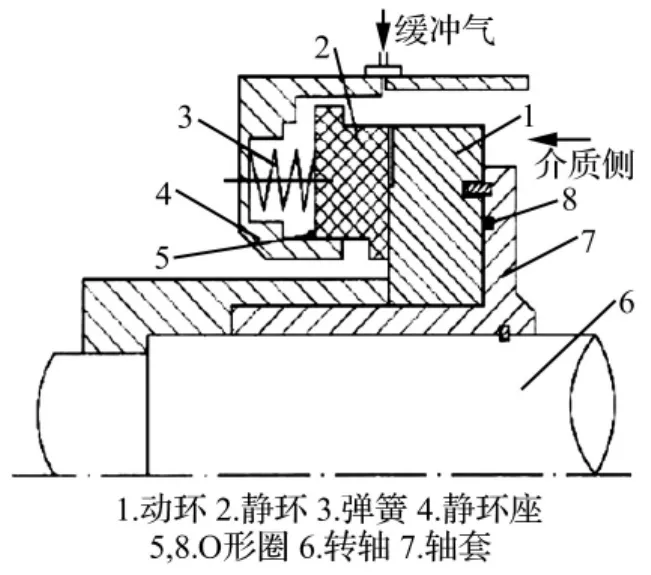
图1 干气密封系统结构分析图Fig.1 Structure analysis fig of the dry gas seal system

图2 静环角向摆动力学模型图Fig.2 Mechanic model of the static ring with angular wobbly

角向摆动稳定性条件［10］:静环摆动惯量J应不大于气膜－密封环系统临界转动惯量Jcr，

即:

式中:静环摆动惯量:

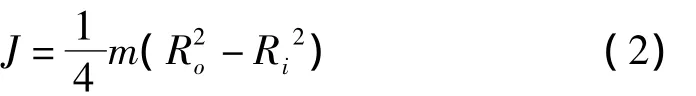
1.1 临界转动惯量Jcr的计算

气膜－密封环系统临界转动惯量Jcr表达式为:

由文［7］得:

则:

1.2 角向摆动刚度K*的计算

应用PH线性化方法及变分运算干气密封螺旋槽内瞬态微尺度流动场的非线性雷诺方程，得到了气膜角向涡动刚度的解析式。继而利用复数转换和迭代法对稳态下气膜边值问题进行求解，求得了气膜涡动刚度的近似解析解［7］。

无量纲气膜角向刚度:

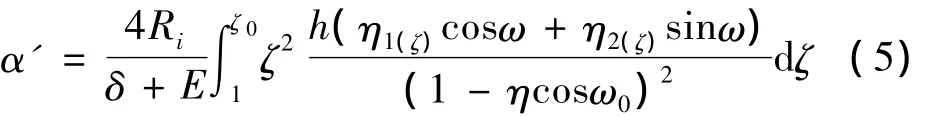
式中:

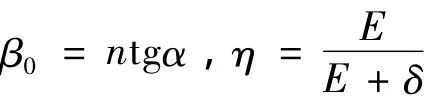
式中各符号的含义:

A，A1，A2，B，B1，B2，C10，C11，C20，C21:积分常数;E:槽深之半，m;n:螺旋槽数;P0:内外介质压力之比;α:螺旋角，rad;βo:槽斜度系数;δ:两密封环间隙，m;ε:迭代摄动小参数;η:槽深度变化的相对幅度;η1、η2:实部、虚部无量纲气膜压力表达式;ζ:无量纲极径;ζ0:无量纲外径;φ:无量纲极角;ω:当量螺旋角，弧度;ω0:φ=0时的当量螺旋角。

气膜角向摆动刚度:

2 角向摆动的运动方程

对静环2个自由度角向扰动，有如下量纲的运动方程:

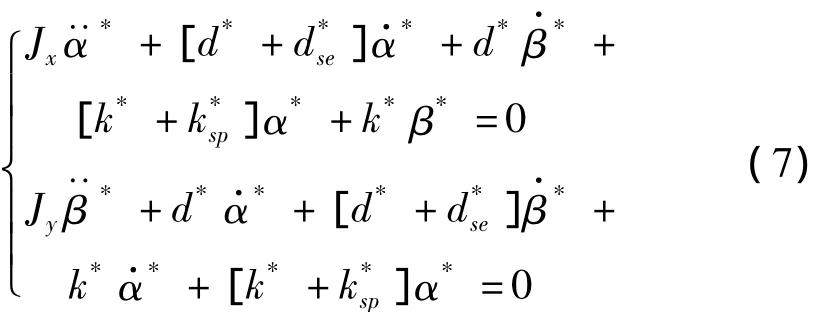
式中:Jx，Jy——静环绕 x 、y轴的摆动惯量(因对称有Jx=Jy=J)

k*，d*——密封气膜在相应角向的恢复力矩刚度，恢复力矩阻尼

α*，β*分别为静环绕x、y轴摆动角度。

3 角向摆动的数值仿真

选取文献［12］中实验参数:实验气体为空气，内径Ri=58.42 mm，外径 R0=77.78 mm，介质压力 p0=4.5852 MPa，环境压力 pi=0.1013 MPa，螺旋槽数 n=10，螺旋角 α =75°，转速 nr=10380 r/min，粘度 μ =1.8 ×10－5Pa·s，槽深 2E=5 μm，密封间隙(气膜厚度)δ=3.05 μm。

3.1 稳定区域的确定

螺旋槽形几何参数包括螺旋角、槽深比、槽数、槽台宽比、和槽长坝长比。这些参数对稳定性的影响是不同的，我们在干气密封螺旋槽润滑气膜的稳定性分析［6，7］中发现螺旋角、槽深比对稳定性的影响较敏感，其中以螺旋角的影响最为显著。因此本文由角向摆动稳定性条件J≤Jcr，寻求螺旋角、槽深比的稳定区域。通过龙格－库塔法对式(4)～式(6)进行近似计算，获得了气膜－密封环系统临界转动惯量Jcr与槽深比η、螺旋角α的三维关系曲面图3。从图3中变化曲面可知α对Jcr的影响较敏感，α的微小变化可引起Jcr的较大变化。在静态优化出的螺旋角范围(60°～80°)内，存在着非连续的稳定区域。

为了更清楚地显示实验条件下的稳定区域，采用了二维坐标图Jcr－α和Jcr－η来表示，η=0.45时，在螺旋角α=75°邻域内的Jcr与α的关系图4;α=75°，在 η=0.3～0.7范围内的 Jcr与 η关系图5。

图3 气膜刚度与α，η关系图Fig.3 Relationship of Jcr，α and η

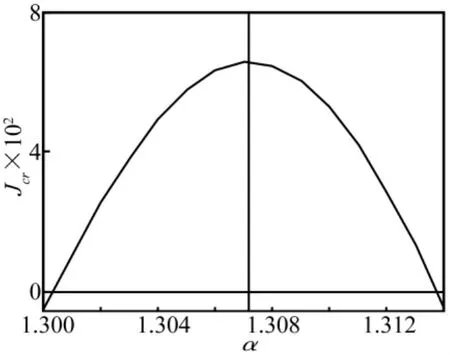
图4 Jcr与α的关系图(η=0.45)Fig.4 Relationship of Jcr，and α(η = 0.45)

图5 Jcr与η的关系图(α=75°)Fig.5 Relationship of Jcrand η(α = 75°)

利用静环摆动惯量计算式(2)求得J=2.637×10－5kg·m2，由角向摆动稳定性条件 J≤Jcr，从图4中可得出:在螺旋角α=75°左右邻域内存在2个失稳临界点，其螺旋角分别为 αcr1=1.3003 rad=74°32'22″和αcr2=1.3137 rad=75°16'09″，介于两者之间的区域为稳定区域;从图5中可得出:在螺旋角α=75°时，由于Jcr大于J，不论η如何变化，均不会发生失稳现象。

3.2 最佳稳定点的振动响应

从图4中知Jcr最大值处为最佳稳定点，该点所对应的螺旋角为 αopt=1.30719181 rad=74°53'48″。利用龙格－库塔法求解角向摆动的二维振动方程(7)，获得了静环绕x轴摆动角度α*的时间历程图6，从图知摆动角度的振幅为5.5×10－6rad，其摆动最大位移为0.4 μm，很显然其值远小于密封间隙(气膜厚度)δ=3.05 μm，证明是稳定的。

3.3 临界点的振动响应

失稳临界点螺旋角 αcr1=1.3003 rad=74°32'22″弧度的振动分析:利用龙格－库塔法求解角向摆动的二维振动方程(7)，在摆角α*的相轨图中出现了振动混沌现象如图7，相轨图中存在混沌吸引子，摆动角度的振幅为 1.0 ×10－4rad，其摆动最大位移为 7.78 μm，很显然其值远大于密封间隙(气膜厚度)δ=3.05 μm，证明是失稳的。将导致密封动静环相互碰撞，这是由于气膜－密封环系统临界转动惯量Jcr等于静环摆动惯量J时系统发生共振所致。

图6 螺旋角αopt=1.30719181 rad最佳稳定点的时间历程图(α*－t)Fig.6 Time history plot of best stability point for spiral angle αopt=1.30719181 rad(α*－t)

图7 螺旋角αcr1=1.3003 rad失稳点的α*相轨图、Pocare映射图和时程图Fig.7 Phase plane，poincare maps and time history plot of instability plot for spiral angle αcr1=1.3003 rad

4 结论

本文建立了密封系统角向摆动的稳定性条件，通过特例的稳定性分析和振动响应，获得了螺旋角的稳定和失稳范围，并对稳定点和临界点进行了振动响应分析。在特例螺旋角α=75°邻域内，存在着稳定区域α =74°30'06″～75°16'10″，其最佳值为 αopt=74°53'48″，最佳稳定点振动响应为准周期运动，而临界点振动响应发生了混沌运动。今后可通过该无量纲通用程序进行角向摆动分析获得螺旋角的稳定范围，为干气密封的优化设计提供理论指导。

［1］曹登峰，宋鹏云，李 伟，等.螺旋槽气体端面密封动力学研究进展［J］.润滑与密封，2006，05:178－182.

［2］Zhang Haojiong，Miller B A，Lander R G.Nonlinear modeling of mechanical gas face seal systems using proper orthogonal decomposition［J］.Journal of Tribology，2006，128(10):817－827.

［3］刘雨川，徐万孚，王之栎，等，端面气膜密封动力特性系数的计算［J］.清华大学学报(自然科学版)，2002，42(2):185－189.

［4］Mi1ler B，Green I.On the stability of gas lubricatedtriboelements using the step jump method［J］.ASME J Lubri，1997，119(1):193 －199.

［5］李双喜，蔡纪宁，陈 罕，等.高速螺旋槽气体密封轴向微扰的有限元分析［J］.北京化工大学学报，2003，30(1):52－56.

［6］杜兆年，丁雪兴，俞树荣，等.轴向微扰下干气密封螺旋槽润滑气膜的稳定性分析［J］.润滑与密封，2006(10):127－130.

［7］丁雪兴，王 悦，张伟政，等.螺旋槽干气密封润滑气膜角向涡动的稳定性分析［J］.北京化工大学学报，2008，35(2):82－86.

［8］Etsion I，An analysis of mechanical face seal vibration.Transactions of the ASME［J］.Journal of Lubrication Technology，1981，103(4):428 －435.

［9］Etsion I，Burton R A.Observation of self-excited wobble in face seals.Transactions of the ASME［J］.Journal of Lubrication Technology，1979(4):101:526－528.

［10］刘雨川，徐万孚，王之栎，等.气膜端面密封角向摆动自振稳定性［J］.机械工程学报，2002，38(4):1－6.

［11］徐万孚，刘雨川，王之栎，等，端面流体膜密封角向摆动自振产生及其半频特性的阐释［J］.机械工程学报，2002，38(9):43－46.

［12］Gabriel R P.Fundamentals of spiral Groove non-contacting Face seals［J］.Lubrication Engnineering，1994，50(3):215 －224.