既有钢筋混凝土Π梁正截面抗弯承载力研究

吕毅刚，张建仁，彭 晖，张克波

(长沙理工大学 土木与建筑学院，湖南 长沙，410114)

自20世纪50年代以来，我国建造了大批钢筋混凝土简支梁桥，采用的设计荷载标准大多为汽-13、挂-60以及汽-20、挂-100。由于荷载过大、材料劣化、环境恶劣、车辆超重以及养护不当等因素，导致桥梁结构性能加速退化及承载力降低，影响桥梁的使用性能。我国许多桥梁已面临着进入“老龄”阶段的问题[1]。部分桥梁早已出现各种“病害”，处于长期带病超负荷状态，随着时间的增长，桥梁老化、损伤的数量和程度都在递增，潜伏着巨大的危险。由于既有桥梁结构性能的退化及实际通行荷载越来越大，为了确保桥梁的安全运营，许多发达国家都致力于研究如何评估桥梁的承载力，将桥梁建设的重点由建造新桥转向对旧桥的加固、改造，以期望延长桥梁的寿命和增加其承载力[2-5]。Jorgensen等[6]对美国的北达科他州1座服役10 a的钢筋混凝土板桥进行了破坏性试验研究，结果表明该桥的实际极限承载力高于理论值。Miller等[7]对美国俄亥俄州1座服役多年的钢筋混凝土板桥进行了破坏性试验，发现已有的结构承载力低于结构实际承载力。马文祥[8]对 1座旧桥进行了现场加载试验，通过一系列测试参数，估算出截面的正截面抗弯承载力。包龙生等[9]基于混凝土桥梁结构的主要损伤，提出了一种承载力评估方法，从而预测桥梁结构的承载能力。周枚等[10]分析了截面弯矩、受压区高度等之间的相互关系，提出了以承载力储备因子来评定桥梁结构的承载能力。Teng等[11]分析了截面配筋率、钢筋锈蚀程度对锈蚀钢筋混凝土梁抗弯承载力的影响。沈德建等[12]建立锈蚀混凝土梁钢筋强度利用系数的计算公式，提出一种锈蚀钢筋混凝土梁抗弯承载力计算方法。在旧桥中，钢筋混凝土简支Π梁桥占有一定的比例。这类桥梁各主梁之间的横向联系很弱，甚至完全没有横向联系，常存在单板受力的状况，钢筋混凝土简支Π梁桥一般都比其他截面类型的钢筋混凝土简支梁桥损伤更严重，承载能力明显下降，这给桥梁的安全运营埋下了极大的隐患；因此，开展对Π梁桥的承载能力研究具有非常重要的理论意义和现实意义。

1 钢筋锈蚀退化性能

混凝土结构中钢筋锈蚀是影响整个结构耐久性的最主要因素。钢筋混凝土桥梁结构或构件在不利环境下引起钢筋锈蚀，从而导致结构性能退化、承载能力下降[13-15]。钢筋锈蚀不但引起其本身物理力学性能发生改变，而且会影响其周围混凝土材料的物理力学性能改变，最终影响桥梁结构的力学性能。在对劣化钢筋混凝土性能的研究中，其中钢筋与混凝土的黏结性能退化为研究的热点。通常把无锈蚀构件的正截面抗弯承载力乘以 1个系数，来计算黏结性能退化的影响[16-19]。现有混凝土结构理论认为钢筋混凝土受弯梁从加载开始到破坏，钢筋及混凝土应变满足变形协调条件，即满足平截面假定。但在劣化的钢筋混凝土受弯梁中，钢筋锈蚀将引起钢筋和混凝土之间的黏结性能退化[20]，增大钢筋和混凝土之间的相对滑移，而与平截面假定有一定程度的误差[16]；因此，对劣化构件进行正截面抗弯承载能力分析时，应考虑到钢筋和混凝土黏结滑移导致的应变差异，建立锈蚀构件的正截面抗弯承载能力计算模型[20-22]。

1.1 钢筋截面锈蚀率

钢筋锈蚀可用截面损失来度量对应钢筋截面锈蚀率。截面锈蚀率反映锈蚀对截面积损害的最大程度，更能真实地反映钢筋锈蚀程度。截面锈蚀率为：

式中：λ为最薄弱截面损失率；Amin为锈蚀后钢筋最薄弱截面面积(mm2)；A0为未锈蚀钢筋截面积(mm2)。

1.2 钢筋锈蚀对屈服强度和极限强度的影响

通过快速锈蚀及旧桥拆除，获得了335根锈蚀钢筋，作为样本[23]。用天平称量锈后钢筋样本质量，并测量样本的直径，用万能试验机对样本进行拉伸试验(图1)。为简化计算，假定钢筋发生均匀锈蚀，获得了锈蚀钢筋样本的屈服强度及极限强度(图1)。

图1 截面锈蚀率与屈服强度和极限强度的关系Fig.1 Relationship among cross-sectional corrosion rate and yield and ultimate strength

定义：

式中：fy0和fu0分别为钢筋锈蚀前的屈服强度和极限强度；fy和fu分别为钢筋锈蚀后的屈服强度和极限强度；ηy为锈后钢筋的屈服强度与初始屈服强度比；ηu为锈后钢筋的极限强度与初始极限强度比。

对这批样本的散点进行回归分析，进行数值拟合，得到截面锈蚀率与屈服(或极限)强度关系：

2 钢筋与混凝土之间的应变关系

为了表示钢筋和混凝土之间的应变关系，定义应变协调函数：

式中：φ(λ)为应变协调函数；εs为钢筋的应变；εcs为钢筋位置处混凝土的应变；λ为钢筋截面锈蚀率。

在极限弯矩作用下，分别将试验得到的不同锈蚀率的螺纹和光圆钢筋梁的跨中截面处的φ(λ)，采用一阶指数拟合，对散点进行回归分析，应变协调函数拟合曲线如下。

螺纹钢筋： φ (λ) = 0 .474 + 0 .924eλ9.679，相关系数R=0.931 2。

光圆钢筋： φ (λ) = 0 .486 + 0 .49eλ4.488，相关系数R=0.957 5。

在理论分析中，Π梁需按照等效的方式转化为T梁进行计算。以下按照T梁进行推导。

3 劣化钢筋混凝土T梁正截面抗弯承载力的计算

T梁截面高度为 h，T肋宽度为 b，翼板有效宽度为fb′，翼板高度为fh。混凝土受压区选用二次抛物线加直线的应力应变关系曲线[24]，引入无量纲参数β(β=x/xc)和γ，用等效矩形的混凝土压力图来代替实际的混凝土压力分布图形。若混凝土标号小于50号，则β取0.8[25]；γ为矩形压力图的应力与受压区混凝土最大应力 σ0的比，即 γ=fcd/σ0(其中，fcd为混凝土轴心抗压强度)。混凝土峰值压应变ε0取0.002，极限压应变εcu取 0.003 3[26]。

3.1 T形梁截面类型判别

判别T形截面类型见图2，若满足：

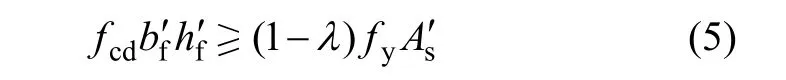
则属于第1类T形截面；反之，属于第2类T形截面。式中：sA′为受拉区锈蚀钢筋的截面面积。

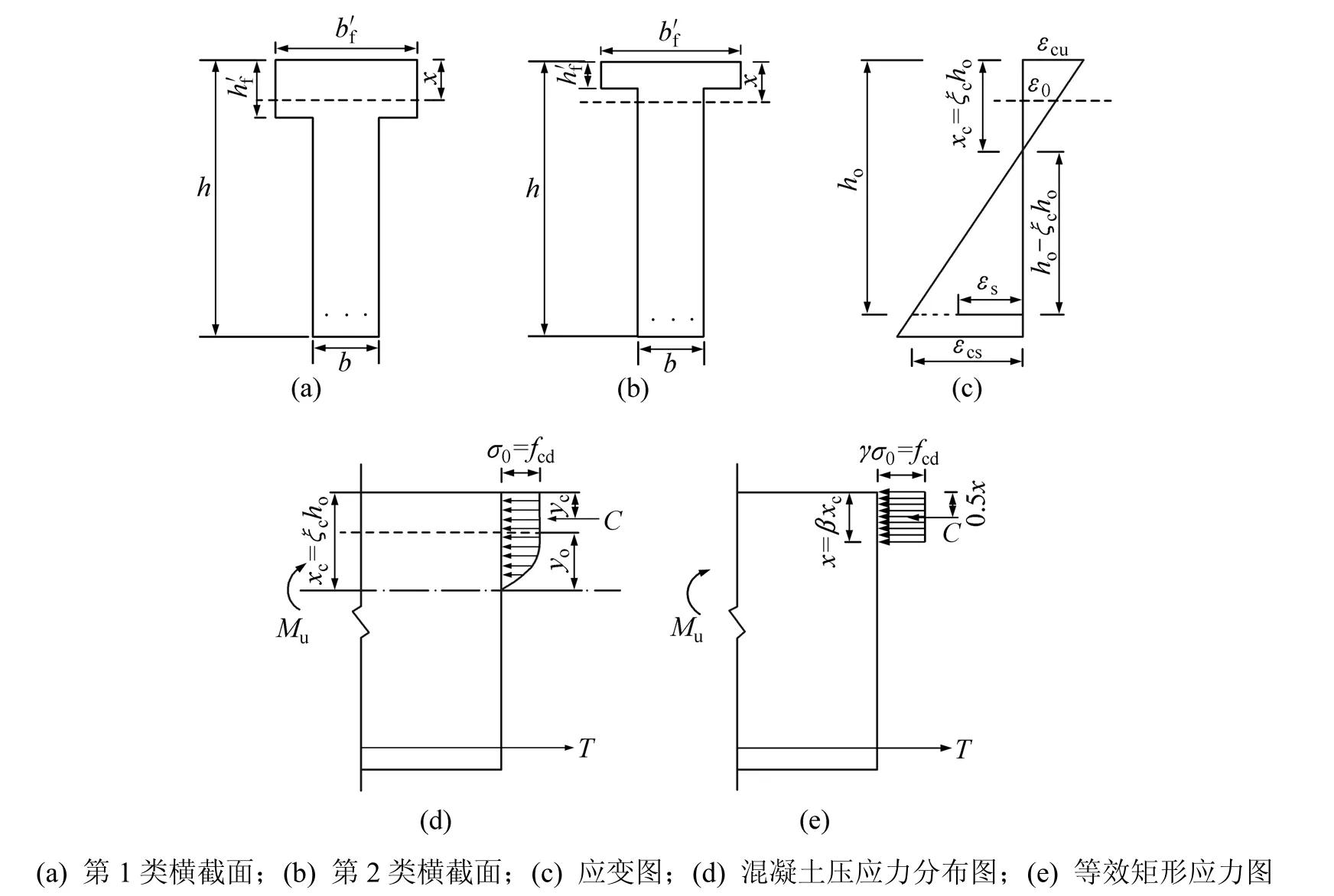
图2 T形截面梁计算图式Fig.2 Calculation schematic for T-shaped section

3.2 受压区高度x的计算

3.2.1 第1类T形截面

第1类T形截面梁计算图式见图2。等效矩形压应力图形的合力C为：

式中：Es为受拉钢筋弹性模量。

根据平截面假定，得：

将式(8)确定的 εs代入式(7)，再根据 β=x/xc及C=T，得到计算受压区高度x的表达式：

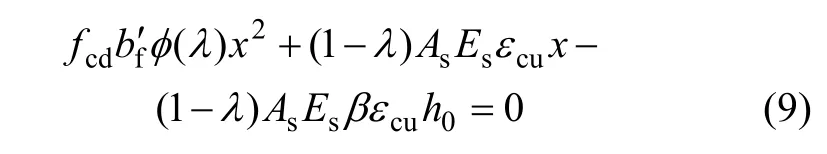
3.2.2 第2类T形截面

根据平截面假定，可以得到：

将式(12)确定的 εs代入式(11)，再根据 β=x/xc及C=T，得到计算受压区高度x的表达式：

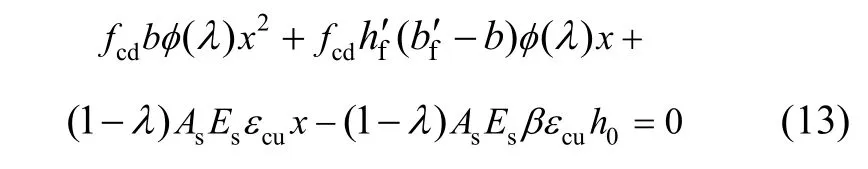
3.3 正截面抗弯承载力Mu的计算

在计算劣化钢筋混凝土梁正截面抗弯承载力时，根据受压区高度 x及式(7)～(9)或式(11)～(13)，可计算极限弯矩状态下钢筋的应变 εs，将 εs与式(2)～(3)确定的锈蚀钢筋屈服时的应变fy/Es进行比较，若εs≥fy/Es，则为适筋梁破坏；反之，则为“锈蚀超筋梁”破坏。

3.3.1 第1类T形截面

第一术，“短板论”。我告诉学生，“短板论”意即一个水桶装水的容量是由最短的那块木板决定的，而高考的总成绩也将由最弱的一科决定。如果语文瘸腿，对高考就如一颗定时炸弹，会砸了十二年的高考梦。在强调理论的同时，我让学生算数，去年高考广东文科重点线是520分，学生先预估其他科目自己最理想的分数，然后再算出语文要拿多少分才能上线。比如，班里有个中等成绩的学生是这么预估的：

由式(9)得到劣化钢筋混凝土梁的计算受压区高度x后，计算并判断钢筋是否屈服。若混凝土被压碎，钢筋已屈服，则需将钢筋屈服强度提供的拉力代入：

根据式(14)，重新计算受压区高度x。

对受压区的混凝土合力C作用点取力矩，可得到计算截面的极限抗弯承载力Mu：

若为“锈蚀超筋梁”破坏，则根据由第1次计算得到的受压区高度x，对受拉锈蚀钢筋合力T取力矩计算 Mu(此时钢筋拉力 T未知，当发生“锈蚀超筋梁”破坏时，不可对受压区混凝土合力 C作用点取力矩)：

3.3.2 第2类T形截面

由式(13)得到劣化钢筋混凝土梁的计算受压区高度x后，计算并判断钢筋是否屈服。若混凝土被压碎时，钢筋已屈服，则需将钢筋屈服强度提供的拉力代入：

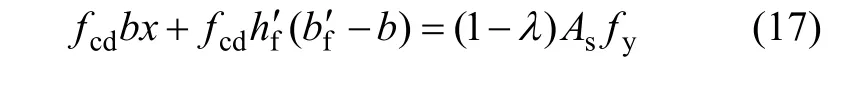
根据式(17)，重新计算受压区高度x。

对压区混凝土合力C作用点取力矩，可得到计算截面的极限抗弯承载力Mu：

若为“锈蚀超筋梁”破坏，则根据由第1次计算得到的受压区高度x，对受拉锈蚀钢筋合力T取力矩计算 Mu(此时钢筋拉力 T未知，发生“锈蚀超筋梁”破坏时，不可对受压区混凝土合力 C作用点取力矩)：

4 工程实例

4.1 试验简介

已服役约40 a的姜公桥[27]，位于湖南省宁乡县境内，为1跨8 m的钢筋混凝土简支Π梁桥。因受自然环境的影响，并长期处于超载工作状态，该桥病害发展严重，桥面大面积破损，扩大基础基底冲刷严重，鉴于其已不满足目前的使用要求，打算将原桥全部拆除重建新桥。为评估旧桥的长期使用承载性能，从现场取3片Π梁，运回实验室重新安装、定位，利用加载系统测试Π梁的正截面抗弯承载力。采用钢卷尺对截面实际尺寸进行量测，Π梁宽1.05 m，高0.66 m，肋宽0.15 m。Π梁横截面布置见图3。

为了模拟Π梁的实际受力状态，采用特制的千斤顶-反力架系统加载，采用在L/3和2L/3共2处同步加载。在每个加载点放置3个千斤顶。

图3 Π梁横截面布置Fig.3 Configuration of cross-section of Π-shaped beam

为了减小加载过程中的Π梁、加载千斤顶及反力架接触处的摩擦，在千斤顶上放置1块橡胶四氟板，在板上再放置1块不锈钢板。为了保证试验荷载的精度，试验前对同步加载系统进行了严格标定，并且在安装千斤顶和测力传感器时，严格注意千斤顶和传感器的轴线对中和正确操作油泵。

4.2 试验结果

记ΔP为极限荷载计算值Pb与开裂荷载计算值Pe之差，即 ΔP=Pb-Pe。在加载时，荷载按 0.50Pe，0.80Pe，Pe，Pe+0.50ΔP，Pe+0.70ΔP，Pe+0.80ΔP，Pe+0.85ΔP，Pe+0.90ΔP、Pe+0.92ΔP，Pe+0.94ΔP，Pe+0.96ΔP，Pe+0.98ΔP和Pb施加，每级进行挠度、裂纹等测试，视破损情况增减加载级次或变更分级荷载。

4.2.1 挠度测试

竖向挠度测点布置见图 4。试验完毕后，每片梁的荷载-挠度曲线见图5。据图5可知：Π梁的竖向挠度测试结果一致性较好，最大竖向挠度发生在梁的跨中位置。

4.2.2 破坏形态

在3片Π梁的加载过程中，钢筋的应变测试结果见图6。由图6可见：当每一个千斤顶荷载大于80 kN，即单点荷载大于240 kN时，一侧腹板底部的受拉钢筋出现明显的应变屈服现象；接近破坏荷载时，对应位置的顶板出现横向裂缝，由于这些裂缝的延伸、加宽，贯通整个横截面而丧失承载力，梁的破坏基本符合适筋梁受弯破坏特点，如2号Π梁的破坏，破坏前裂缝宽度超过10 mm。

图4 Π梁挠度测点布置Fig.4 Measurement planning of Π-shaped beam

图5 梁竖向挠度随荷载图变化Fig.5 Relationship between vertical deflection and load for three kinds of beam

4.2.3 正截面抗弯承载力结果分析

这座桥由于年代久远，所有资料已经丢失，试验后，选取相应位置钻取混凝土芯样，通过抗压试验得到混凝土芯样的抗压强度，用酚酞溶剂测试混凝土的碳化深度；此外，从Π梁的两侧腹板取出受拉主筋，用游标卡尺量测钢筋直径，得出钢筋截面锈蚀率和钢筋材料力学性能，见表1(对直径为22.0 mm的钢筋，屈服强度为293.4 MPa，极限强度为440.3 MPa；对直径为24.0 mm的钢筋，屈服强度为252.1 MPa，极限强度为393.3 MPa)。

在理论计算中，把Π梁转化成等效的T梁，采用同步加载及利用上述理论公式进行计算，3片Π梁各自的单点极限荷载实测值和理论值见表2。从表2可见：各自的极限荷载相近。

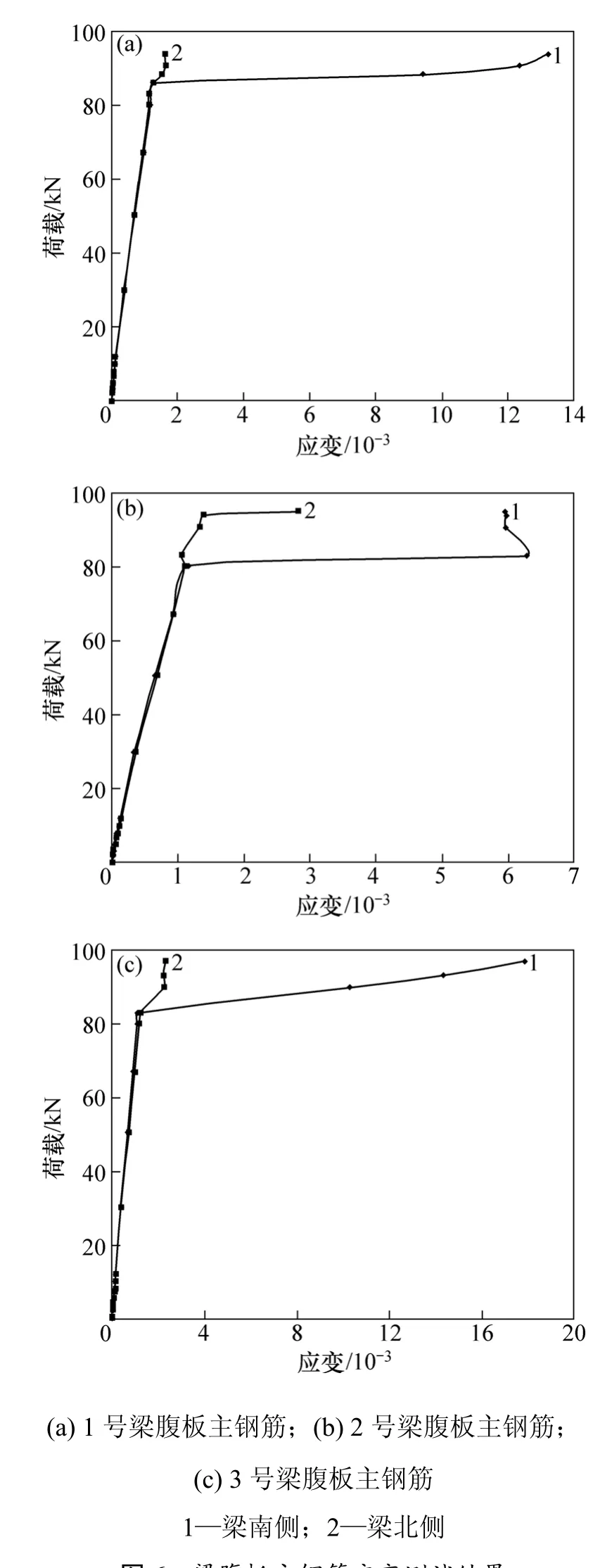
图6 梁腹板主钢筋应变测试结果Fig.6 Strains of main rebars of web for beams

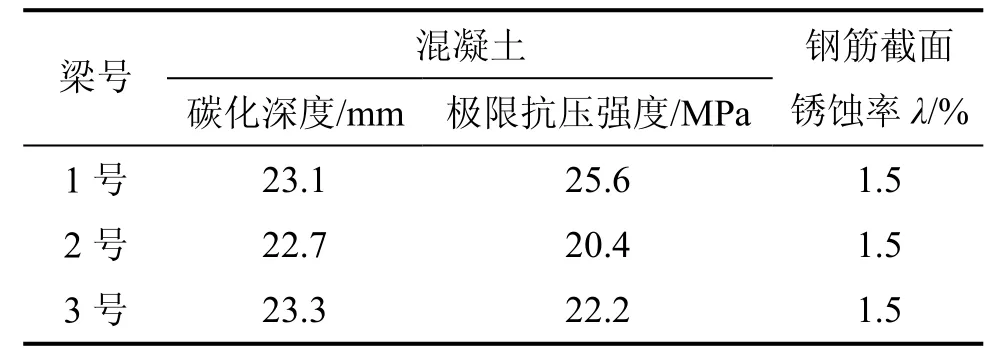
表1 桥梁材质检测结果Table1 Inspection results of materials quality

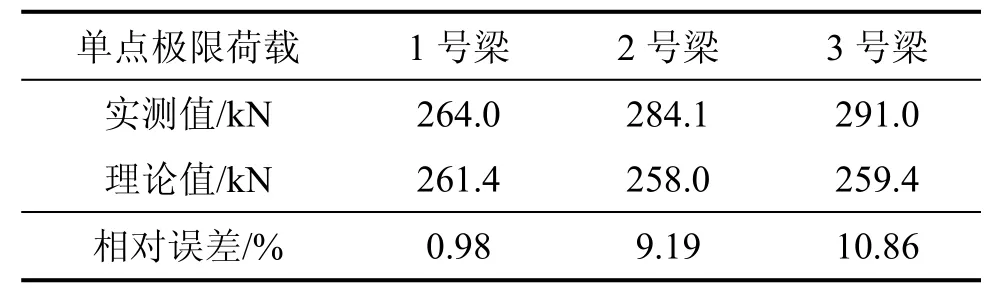
表2 Π梁极限荷载Table2 Ultimate load of Π-shaped beam

5 结论

(1) 在既有钢筋混凝土Π梁桥中，钢筋锈蚀等引起钢筋与混凝土之间的应变协调关系并不完全符合平截面假定。

(2) 在平截面假定不成立的前提下，建立了考虑材料性能退化以及钢筋与混凝土应变不协调性的正截面力学模型，提出了不同锈蚀率下既有钢筋混凝土Π梁的正截面抗弯承载力计算公式。

(3) 对服役约40 a的姜公桥Π梁构件进行了抗弯承载能力试验。试验数据表明：采用所推导的承载力计算公式所得计算结果与试验结果较吻合，证明本文提出的极限抗弯承载力计算方法正确、有效。

[1] 张建仁, 彭晖, 张克波, 等. 锈蚀钢筋混凝土旧桥超限及极限荷载作用的现场破坏试验研究[J]. 工程力学, 2009, 26(2):213-224.

ZHANG Jian-ren, PENG Hui, ZHANG Ke-bo, et al. Test study on overload and ultimate behavior of old reinforced concrete bridge through destructive test of corroded bridge[J].Engineering Mechanics, 2009, 26(2): 213-224.

[2] Berto L, Simioni P, Saetta A. Numerical modelling of bond behavior in RC structures affected by reinforcement corrosion[J].Engineering Structures, 2008, 30(5): 1375-1385.

[3] Biondini F, Frangopol D M. Probabilistic limit analysis and lifetime prediction of concrete structures[J]. Struct Infrastruct Eng, 2008, 4(5): 399-412.

[4] Stewart M G, Mullard J A. Spatial time-dependent reliability analysis of corrosion damage and the timing of first repair for RC structures[J]. Engineering Structures, 2007, 29(7): 1457-1464.

[5] Stewart M G. Mechanical behavior of pitting corrosion of flexural and shear reinforcement and its effect on structural reliability of corroding RC beams[J]. Structural Safety, 2009(31):19-30.

[6] Jorgensen J L, Larson W. Field testing of a reinforced concrete highway bridge to collapse[J]. Transportation Research Record,1976, 607(3): 66-80.

[7] Miller R A, Aktan A E, Shahrooz B M. Destructive testing of decommissioned concrete slab bridge[J]. Journal of Structural Engineering, 1994, 120(7): 2176-2198.

[8] 马文祥. 车载试验法评定旧钢筋混凝土连续梁桥承载力[J].兰州铁道学院学报, 1996, 15(1): 20-26.

MA Wen-xiang. Evaluation of bearing capacity of existing reinforced concrete continuous girder bridge by track tests[J].Journal of Lanzhou Railway Institute, 1996, 15(1): 20-26.

[9] 包龙生, 于玲, 黄海, 等. 混凝土桥梁损伤诊断及承载力评估述评[J]. 东北公路, 2003, 26(4): 113-115.

BAO Long-sheng, YU Ling, HUANG Hai, et al. Damage diagnosis and strength evaluation for existing concrete bridges[J].East North Highway, 2003, 26(4): 113-115.

[10] 周枚, 贺拴海, 宋一凡. 基于挠度试验的梁式结构评估[J]. 长安大学学报, 2004, 24(5): 40-47.

ZHOU Mei, HE Shuan-hai, SONG Yi-fan. Structural evaluation for beams based on deflection testing[J]. Journal of Chang’an University: Natural Science Edition, 2004, 24(5): 40-47.

[11] Teng J G, Chen J F, Smith S T, et al. Behavior and strength of FRP-strengthened RC structure: A-state-of-the-art review[J].Structures & Buildings, 2003, 156(1): 51-62.

[12] 沈德建, 吴胜兴. 大气环境下严重锈蚀钢筋混凝土梁力学性能试验研究[J]. 桥梁建设, 2008, 41(11): 1-6.

SHENG De-jian, WU Sheng-xing. Experimental Study of mechanical properties of severely corroded reinforced concrete beams in atmospheric environment[J]. Bridge Construction,2008, 41(11): 1-6.

[13] Cairns J, Dut Y, Law D. Structural performance of corrosion-damaged concrete beams[J]. Magazine of Concrete Research, 2008, 60(5): 359-370.

[14] Yoon S C, Wang K J, Jason W W, et al. Interaction between loading, corrosion, and serviceability of reinforced concrete[J].ACI Materials Journal, 2000, 97(6): 637-644.

[15] Rodriguez J, Ortega L M, Casal J. Load carrying capacity of concrete structures with corroded reinforcement[J]. Construction and Building Materials, 1997, 11(4): 239-248.

[16] 张建仁, 王磊. 既有钢筋混凝土桥梁构件承载力估算方法[J].中国公路学报, 2006, 19(2): 49-55.

ZHANG Jian-ren, WANG Lei. Estimated approach to carrying capacity of existing reinforced concrete bridge member[J]. China Journal of Highway and Transport, 2006, 19(2): 49-55.

[17] ZHENG Yi, LIU Ming, ZHOU Jing-hai, et al. Bonding stress-slip constitutive behavior between bars and grout concrete[J]. Journal of Central South University of Technology,2009, 16(5): 841-844.

[18] Azad A K, Ahmad S, Azher S A. Residual strength of corrosion-damaged reinforced concrete beams[J]. ACI Materials Journal, 2007, 104(1): 40-47.

[19] 牛荻涛, 王庆霖. 锈蚀开裂前混凝土中钢筋锈蚀量的预测模型[J]. 工业建筑, 1996, 26(4): 8-10.

NIU Di-tao, WANG Qing-lin. Prediction model of steel corrosion extent in reinforced concrete structures before producing corrosion crack[J]. Industrial Construction, 1996,26(4): 8-10.

[20] Capozucca R, Nilde C M. Identification of damage in reinforced concrete beams subjected to corrosion[J]. ACI Structural Journal,2000, 97(6): 902-909.

[21] Eyre J R, Nokhasteh M A. Strength of corrosion damaged reinforced concrete slabs and beams[J]. Proceedings of the Institution of Civil Engineers, Structures and Building, 1992,94(2): 197-203.

[22] 王晓刚, 顾祥林, 张伟平. 锈蚀钢筋混凝土梁抗弯性能数值模拟[J]. 建筑科学与工程学报, 2009, 26(1): 49-54.

WANG Xiao-gang, GU Xiang-lin, ZHANG Wei-ping. Numerical simulation of flexural behavior of corroded reinforced concrete beams[J]. Journal of Architecture and Civil Engineering, 2009,26(1): 49-54.

[23] 张克波. 锈蚀 RC构件力学性能与整桥破坏性试验研究[D].长沙: 长沙理工大学土木与建筑学院, 2009: 64-87.

ZHANG Ke-bo. Mchanical behavior of corroded RC element and destructive testing for whole bridge[D]. Changsha:Changsha University of Science & Technology. School of Civil Engineering and Architecture, 2009: 64-87.

[24] 叶见曙. 结构设计原理[J]. 北京: 人民交通出版社, 2005:1-43.

YE Jian-shu. Design principle of structure[J]. Beijing: China Communications Press, 2005: 1-43.

[25] JTG D62—2004. 公路钢筋混凝土及预应力混凝土桥涵设计规范[S].

JTG D62—2004. Code for design of highway reinforced concrete and prestressed concrete bridges and culverts[S].

[26] 周朝阳, 王兴国, 肖菲菲. 先张后粘 FRP的钢筋混凝土构件抗弯能力分析[J]. 中南大学学报: 自然科学版, 2006, 37(1):184-187.

ZHOU Chao-yang, WANG Xing-guo, XIAO Fei-fei. Analysis of flexural capacities for RC members bonded with pre-tensioned FRP[J]. Journal of Central South University: Science and Technology, 2006, 37(1): 184-187.

[27] 钟慧萍, 张建仁, 于洪波. 姜公桥单板破坏性试验研究[J]. 长沙交通学院学报, 2006, 22(1): 2-6.

ZHONG Hui-ping, ZHANG Jian-ren, YU Hong-bo. Study on the simple plate destructive test of Jang-gong bridge[J]. Journal of Changsha Communications University, 2006, 22(1): 2-6.