建筑真空玻璃承载性能及强度设计

刘小根，包亦望，万德田，邱岩，王秀芳，许海凤

(1. 中国建筑材料科学研究总院 检验认证中心，绿色建材国家重点实验室，北京，100024；2. 北京新立基真空玻璃技术有限公司，北京，101111)

建筑真空玻璃承载性能及强度设计

刘小根1，包亦望1，万德田1，邱岩1，王秀芳1，许海凤2

(1. 中国建筑材料科学研究总院 检验认证中心，绿色建材国家重点实验室，北京，100024；2. 北京新立基真空玻璃技术有限公司，北京，101111)

针对真空玻璃在工程应用中的强度设计关键问题，分析均布载荷下真空玻璃的弯曲失效特性及影响因素。通过试验验证，真空玻璃板最大应力分布在中心部位，其应力分布特征可按四边简支理论计算。根据试验结果，给出风载荷作用下真空玻璃的强度设计计算公式及持久应力作用下玻璃的强度设计值。研究结果表明：真空玻璃内外片变形一致，2片玻璃承载比例按其刚度分配，当2片玻璃厚度相同时，其抗外力强度最大；由于真空玻璃存在非均匀内应力，其承载能力约相当于同等厚度普通玻璃的85%；设计真空玻璃承载强度时，必须考虑其表面附加张应力的影响。

真空玻璃；承载特性；支撑应力；持久应力；强度设计

真空玻璃作为新一代节能环保材料，被广泛应用于建筑行业门窗幕墙等隔热保温结构，真空玻璃是今后最具发展潜力的节能玻璃[1−3]。近年来，科研工作者致力于真空玻璃产品的研发，虽然对真空玻璃的隔热保温原理已研究比较透彻[4−7]，但对真空玻璃在应用中所涉及的强度理论和相应的设计及工程可靠性评价还鲜见报道。真空玻璃由内外2块玻璃构成，2块玻璃之间有一定的间距，中间有支撑物，四周用低熔点玻璃密封。对这种特殊结构，工程设计者颇关心外载作用下真空玻璃内、外片变形与承载特性及强度设计问题。本文作者首先通过试验，研究真空玻璃在均布载荷作用下内、外片玻璃的变形协调性能、应力分布特征和极限承载能力；然后，根据试验结果，给出风载荷作用下真空玻璃的强度计算公式及持久应力作用下的强度设计值。

1 试验条件与方法

试验选用的真空玻璃均为北京新立基真空玻璃技术有限公司生产，真空玻璃的长、宽分别为0.51 m和0.36 m，2块基片厚度均为4 mm。真空玻璃承受的均布载荷采用负压方式加载，通过真空泵抽气调节负压，以便对真空玻璃施加不同的均布载荷。预先在真空玻璃内外基片(直接承力面为外片)的外表面不同部位粘贴应变片，以记录玻璃板在均布载荷下的应力分布特征。采用基恩士公司生产的LK−G40激光位移传感器，测量真空玻璃2块基片在均布载荷作用下的变形。该传感器通过入射激光穿过第1块玻璃照射到第2块玻璃表面上，并接收2块玻璃表面反射回来的光线，从而可以同时精确测量到2块玻璃的变形。另外，通过在光弹仪上连接CCD(Charge-coupled device)摄像头，记录从加载到真空玻璃破坏过程中支撑点处的应力光弹斑图，观察受载过程中其内部结构的变形及应力分布变化趋势。

2 结果与分析

2.1 真空玻璃变形协调性能

图1所示为经位移传感器测到的真空玻璃内外2块基片在不同载荷下中心点处的最大挠度分布图。

图1 真空玻璃内外片在不同载荷下的最大挠度Fig.1 Maximum deflection of inner and outer panels of vacuum glazing at various uniform loads

由图1可以看出：即使承受载荷不断变大，2块玻璃的变形均一样，真空玻璃仍保持为一体，说明在外载作用下真空玻璃的2块基片在该处的变形是协调的。另外，由于真空玻璃在大气压作用下，会在支撑物与玻璃表面接触部位产生应力集中，因此，可以借助光弹仪，观察其从受载直至破坏整个过程中各支撑点处的应力光斑变化，了解真空玻璃任何一个支撑点处的应力变化与变形协调。图 2(a)所示为真空玻璃受载前的应力光斑图；图2(b)所示为真空玻璃受载破坏前一瞬间的应力光斑图；图 2(c)所示为破坏后的应力光斑图。从图2可以看出：即使在破坏前一瞬间，真空玻璃的支撑应力光斑图仍与受载前相同，即2片玻璃仍与支撑物相互紧密接触(如变形不协调，则该处应力光斑将消失)，说明真空玻璃在外载作用下2块基片变形十分协调。这是由于真空玻璃中间层是真空层，巨大的大气压差使2块基片与中间的支撑物接触在一起，而真空玻璃受外载作用一般远小于大气压对真空玻璃的作用，因此，2块基片不会因外载作用而导致变形不协调。

2.2 均布载荷作用下真空玻璃的应力分布

2.2.1 真空玻璃载荷传递特性理论分析

真空玻璃的2块基片的四周被低熔点玻璃固定在一起。支撑物只起支撑作用，对接触面不产生面内剪应力和弯矩，因此，在均布载荷作用下，2块基片均按各自的中性层弯曲，中性层在玻璃横截面对称轴上。在外载作用下，直接承受载荷的一块基片将部分载荷由支撑物传递到另一块基片上，此时，2块基片共同分担着外载作用。由于真空玻璃支撑物均匀密集地布置在玻璃板面积内每个部分，每个支撑物受力F基本相同，为简化计算，可将作用于玻璃板分散的支撑力视为均布压力(见图 3)。设外片玻璃受均布载荷q作用，内外片受支撑物作用的等效均布载荷为q0，则外片玻璃在q−q0作用下弯曲，内片玻璃在q0作用下弯曲，由试验结果可知，各支撑点处内外片玻璃挠度变形协调，即

图2 真空玻璃受载过程中的应力光弹斑变化Fig.2 Change of photoelastic fringe in vacuum glazing during loading process

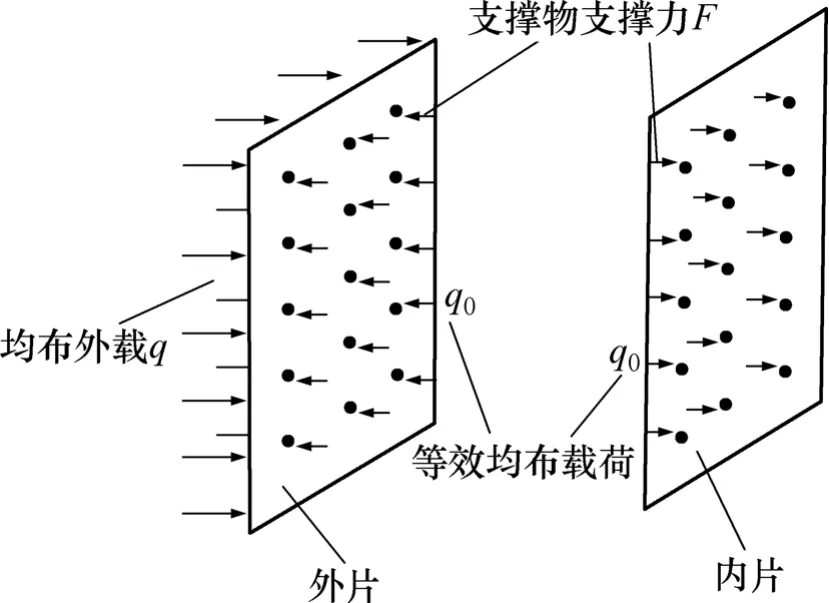
图3 真空玻璃内外片受荷分配示意图Fig.3 Load distribution of inner and outer glass panels of vacuum glazing

式中：w1和w2分别为外、内片玻璃相同位置的挠度。单片玻璃基片挠度按四边固支计算(考虑其边部被熔固在一起)，根据薄板理论，板在均布载荷下的挠度方程为[8]：

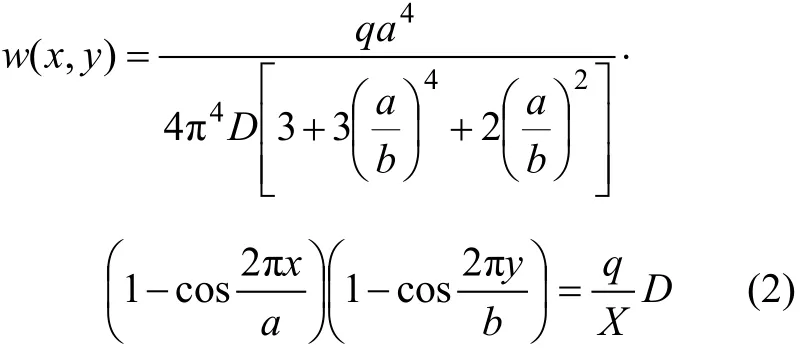
其中：a和b分别为玻璃板的长和宽；q为均布载荷；对于某一固定位置点，X为常数。可见：玻璃在某一固定点的挠度只与玻璃的抗弯刚度D有关。

式中：h为玻璃的厚度；ν为玻璃的泊松比；E为玻璃弹性模量。将内外片玻璃承受的载荷分别代入式(2)并根据式(1)的变形协调关系，得：

即当真空玻璃的2块玻璃基片厚度相等时，相同载荷下真空玻璃对应的最大挠度最小，即相应的最大应力也最小。因此，为使真空玻璃承载能力最佳，在设计真空玻璃结构时，玻璃基片应选择相同厚度。

2.2.2 均布载荷作用下真空玻璃弯曲应力分布

在真空玻璃承载面粘贴应变片，中心及边缘部位测点布置见图4。真空玻璃四边弹性支撑，对真空玻璃施加均布载荷为15 kPa，试验测量结果见表1。

图4 真空玻璃弯曲应力测点布置示意图Fig.4 Sketch of measuring stress point in vacuum glazing

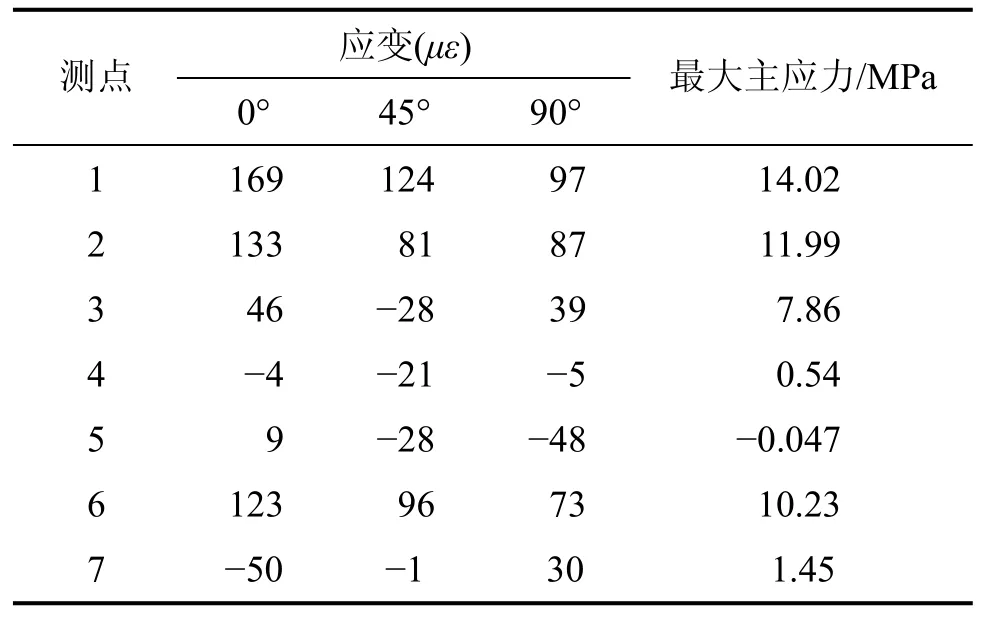
表1 均布载荷下真空玻璃表面各测点的应变及最大弯曲主应力Table 1 Strain and maximum principal on surface of vacuum glazing at uniform loads

由表1可以看出：在四边弹性支撑，均布载荷作用下，真空玻璃的最大弯曲主应力在板中心，边部应力几乎为零(边部应变出现很小的负值，是因真空玻璃边部受到支承件一定的约束作用)。即使真空玻璃2基片边部被封接，外载作用下封接的边缘也不存在应力集中现象，这是由于载荷作用下2块基片边缘能够随着整体变形转动而不受约束，且2基片变形协调，因而在四边弹性支撑下，真空玻璃最大应力仍出现在 2基片板中心，而不在边部。因此，在真空玻璃强度设计时，可将真空玻璃视为一整体板结构，按四边简支理论计算。

2.3 真空玻璃极限承载能力及强度设计

2.3.1 真空玻璃的极限承载能力

通过对6块真空玻璃进行极限承载试验，得到最大载荷及破坏瞬间真空玻璃板中心的最大弯曲应力(主应力)，见表2。

表2 真空玻璃极限载荷及对应的最大弯曲应力Table 2 Ultimate load and corresponding stress of vacuum glazing

由表 2可以看出：真空玻璃的极限破坏载荷在0.04 MPa左右，符合正态分布。应变片记录到的最大弯曲主应力都在50 MPa以下，而普通玻璃的弯曲强度为 50～100 MPa。

真空玻璃在弯曲应力未达到玻璃弯曲强度就被破坏，这主要是真空玻璃的特殊结构所致。在大气压作用下，真空玻璃物支的撑部位玻璃外表面，存在支撑拉应力及挠度。图 5(a)所示为利用有限元分析的真空玻璃支撑应力分布图。文献[9−10]中给出了该部分应力的计算公式，在均布载荷作用下，若不考虑四边熔固作用，则2块基片均按各自的中性层弯曲，真空玻璃最大弯曲应力在2块基片玻璃板中心。图5(b)所示为利用有限元计算的弯曲应力分布云图。最大弯曲应力在板中心与该处支撑应力叠加(见图6)，可引起真空玻璃过早破坏，降低承载性能。

2.3.2 持久应力作用下玻璃强度设计

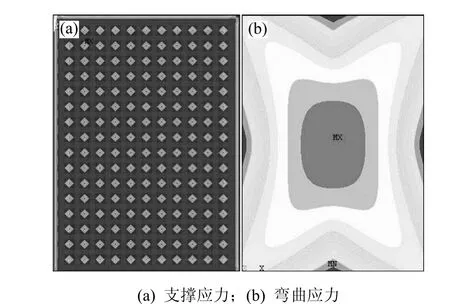
图5 ANSYS分析均布载荷作用下真空玻璃弯曲应力及大气压下支撑应力分布云图Fig.5 Bending stress and supporting stress in vacuum glazing by ANSYS

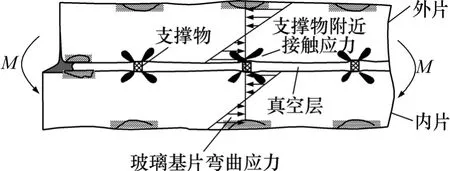
图6 受弯状态下真空玻璃应力分布特征Fig.6 Characteristics distribution of stress in vacuum glazing under bending load

由 Griffich建立的传统的脆性材料裂纹扩展理论表明，裂纹在持续外力下的扩散，取决于表面能是否持续不变。建筑玻璃在使用过程中，在持久应力下，环境中水分及活性介质与玻璃表面反应会引起疲劳破坏，风沙对玻璃表面的磨损也会造成玻璃强度下降[11]。真空玻璃承受的支撑应力属于长期载荷，不仅要承受风雪载荷等可变载荷，还有可能承受地震、爆炸等偶然载荷。因此，真空玻璃的玻璃强度安全系数，除应考虑玻璃强度离散安全系数F1外，还应考虑持久应力作用下的安全系数F2，其综合安全系数F为F1×F2。

(1) 真空玻璃的玻璃强度离散安全系数。玻璃的断裂强度离散性大，其强度的测定与测试条件如加载方式、加载速率、持续时间等密切相关。很多国家往往采用统计分析方法，推断出玻璃强度的估算公式，通常将几百片玻璃破坏的试验结果进行统计处理，求出平均值和标准差，推断玻璃的力学强度，给出设计安全系数与失效概率见表3。

按《玻璃幕墙工程技术规范》(JGJ 102—2003)[12]，玻璃幕墙失效概率为0.1%，真空玻璃的玻璃强度离散安全系数F1为2.5。

(2) 持久应力作用下玻璃的安全系数。持久应力作用可使玻璃失效概率增大。欧洲主要以失效概率确定持久应力作用下玻璃强度的设计值[13]。我国的设计规范虽然给出了玻璃强度的设计值，但没有考虑载荷长期持续作用时间的影响，文献[14]建议长期载荷安全系数F2；按表 4取值，该取值方法较适合真空玻璃[14]。

表3 玻璃安全系数与失效概率Table 3 Safety factor of glass under various failure probability

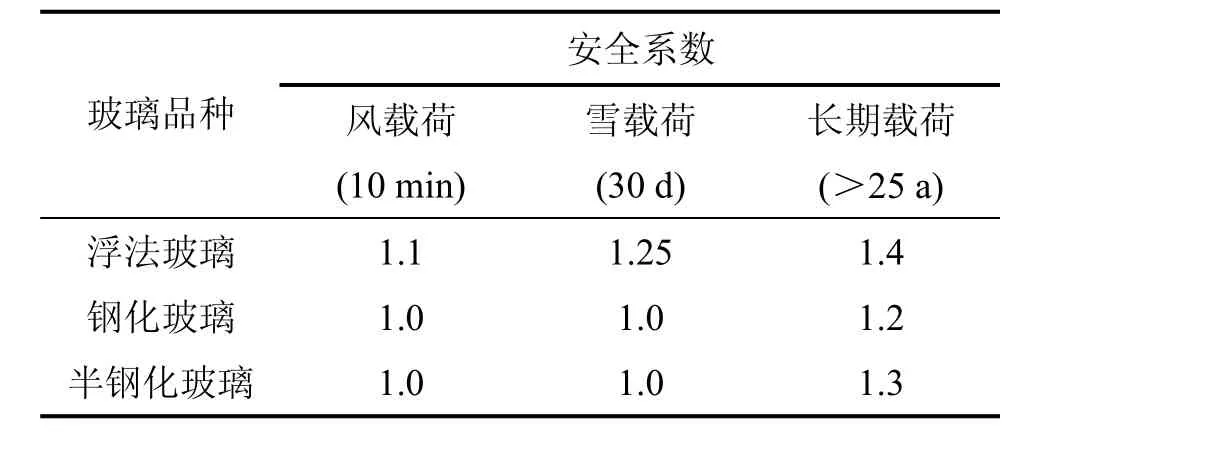
表4 不同持久载荷作用下玻璃的安全系数Table 4 Safety factor of glass under different long-term loads

(3) 真空玻璃强度综合安全系数及强度设计值。根据表3和表4，可以得到玻璃的综合安全系数。按真空玻璃基片玻璃品种，将真空玻璃基片的平均弯曲强度除以综合安全系数，即得真空玻璃的强度设计值，见表 5，其中玻璃的弯曲强度为建筑玻璃应用技术规程(JGJ 113—2003)所规定。

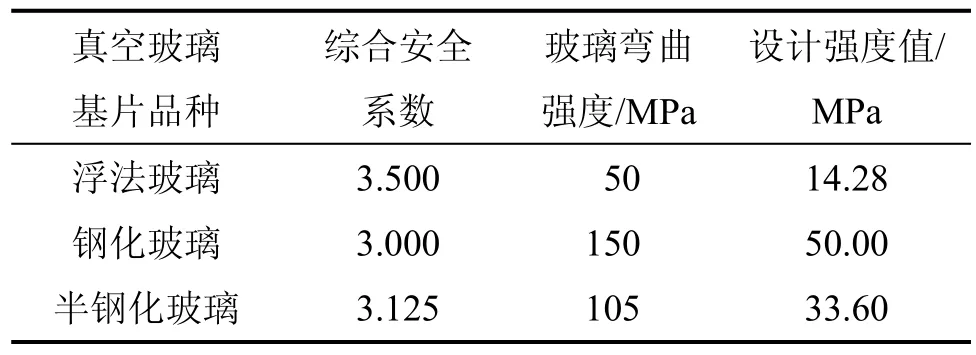
表5 真空玻璃强度综合安全系数及强度设计值Table 5 Comprehensive safety factor and strength design value of vacuum glazing panes

2.3.3 真空玻璃抗风压设计

采用等效厚度计算玻璃的承载能力可简化设计程序。虽然真空玻璃由2块基片玻璃构成，并且每块基片玻璃均有各自的中性层，但根据前面的分析，外载作用下真空玻璃的2块基片变形协调，四边支承真空玻璃表面弯曲应力分布特征与四边简支板相同；因此，在真空玻璃承载强度计算时，可将真空玻璃当作1块整体，采用等效厚度替代真空玻璃的总厚度。当2块玻璃完全不受另一片玻璃约束时，相当于2块玻璃简单叠加在一起，根据变形协调，应力等效厚度为。当2块玻璃紧密结合如同一整块单层玻璃，等效厚度为2块玻璃的总厚度之和heq=h1+h2。因真空玻璃2块基片的四周被熔封玻璃固接在一起，中间又有支撑物传力，因此，其应力等效厚度处于这两者之间(当h1=h2时，heq=(0.63～1.00)h，其中h=h1+h2)。

由于真空玻璃结构复杂，无法采用理论计算得出真空玻璃的等效厚度。通过试验，获得在载荷作用下真空玻璃和相同面积普通玻璃的最大弯曲挠度和应力分布状况，见图7。由图7可以看出：与同样厚度的普通玻璃相比(例如4 mm+4 mm的真空玻璃与8 mm的普通玻璃相比)，在相同载荷下，真空玻璃的最大挠度和应力均比普通玻璃的大。即真空玻璃的承载能力比同等厚度的普通玻璃的小，总厚度为8 mm的真空玻璃与7 mm的普通玻璃承载能力相当。所以，对真空玻璃进行抗风压设计时，总厚度而应采用一个折算厚度(等效厚度)。

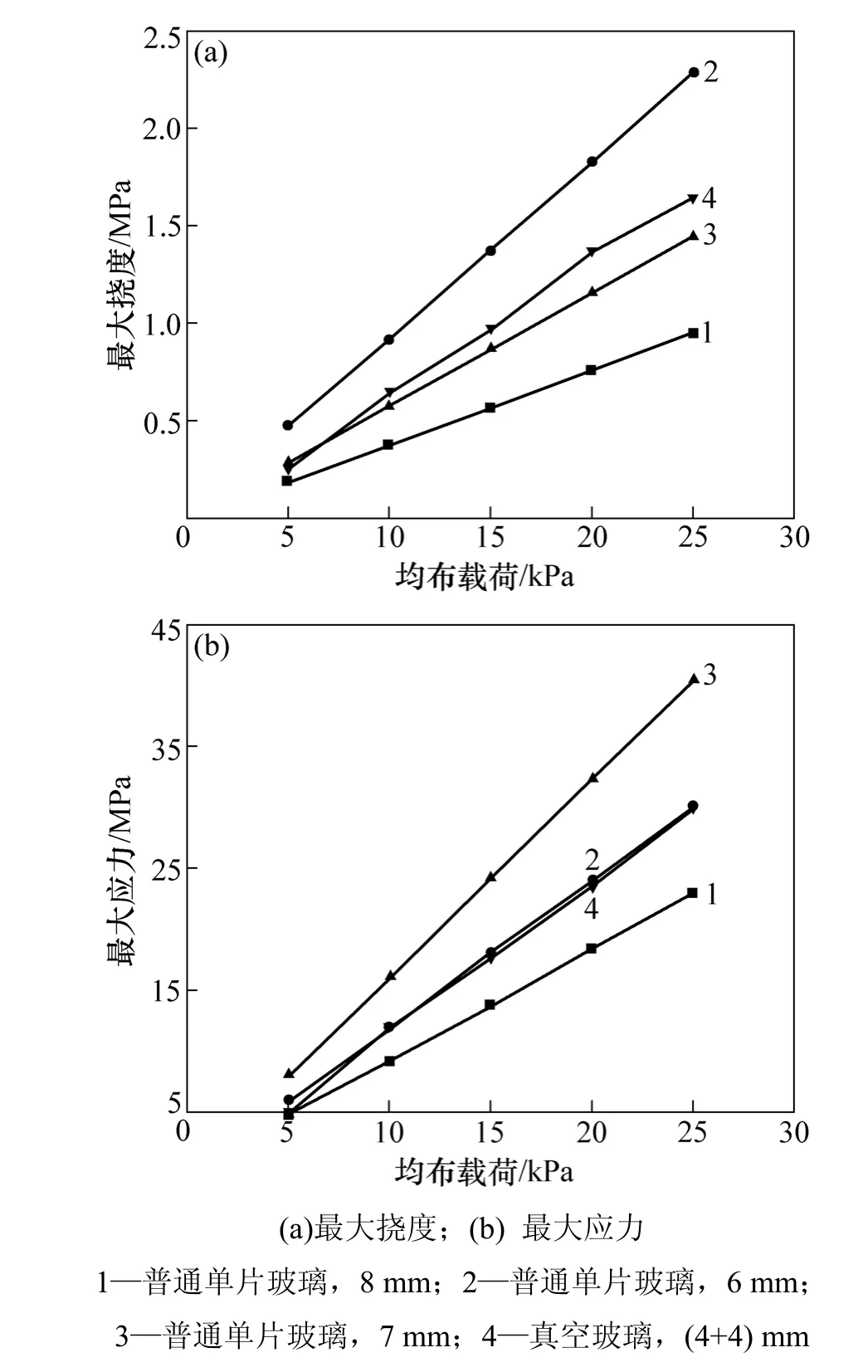
图7 真空玻璃与普通玻璃受载下最大挠度与应力对比图Fig.7 Comparison of maximum stress and deflection between the vacuum glazing and common glass

工程设计时，可参考规范中的普通玻璃的设计方法。对于四边弹性支撑的真空玻璃门窗或幕墙，按我国目前的设计规范，采用最大应力设计时，玻璃板中心的最大应力计算公式为[15]：

其中：σ为风载荷作用下玻璃的最大弯曲应力，MPa；q为风载荷设计值，MPa；h为玻璃板厚度，mm；φ为弯曲系数，与边长比a/b有关。

对四边支承的真空玻璃，可应用上面计算公式，真空玻璃表面最大拉应力为最大弯曲应力与大气压作用下其外表面最大支撑拉应力之和，其厚度应按2块基片玻璃总厚度乘以折算系数。因此，

其中：σmax为真空玻璃表面最大拉应力，其值不得超过表5中的玻璃强度设计值；η为真空玻璃厚度折算系数，根据试验结果取值为0.85；h为真空玻璃2块基片厚度之和；σ0max为大气压作用下真空玻璃外表面最大支撑拉应力，其计算公式为[10]：

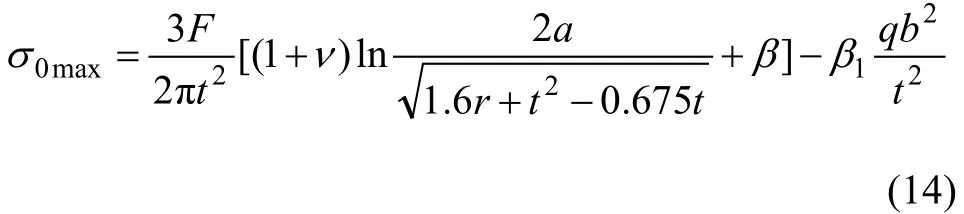
其中：a和b分别为真空玻璃支撑点的横向和纵向距离；t为玻璃基片厚度；r为支撑物半径；α，β和β1与a/b有关。真空玻璃在不受任何载荷作用下，F=q0ab(q0为大气压)。但当承受外部均布载荷q时，当真空玻璃2块基片厚度相等，此时，有q/2的外载通过支撑物传递给另一块基片玻璃(正压状态下)，因此，此时支撑物总支撑力为：

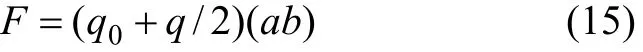
将式(15)代入式(14)可得到风载荷作用下真空玻璃最大支撑拉应力σ0max，最后将σ0max代入式(13)，即可得到各种综合因素影响下真空玻璃的最大设计风载荷。

3 结论

(1) 真空玻璃内外片玻璃变形协调，2块基片玻璃承载比例按其刚度分配，当2块基片玻璃厚度相同时，真空玻璃能够达到最优抗外力能力。

(2) 四边弹性支承真空玻璃最大应力分布在 2块基片玻璃板中心，在进行四边支承的真空玻璃门窗幕墙强度设计时，可将真空玻璃视为一整体，按四边简支理论计算。

(3) 当真空玻璃等效厚度为真空玻璃总厚度的85%时，真空玻璃强度设计需考虑大气压作用下玻璃表面支撑张应力的影响，真空玻璃安全系数需按持久应力作用下的玻璃综合安全系数选取。

[1]唐健正. 真空玻璃产业化现状及发展前景[J]. 玻璃, 2008,203(8): 26−36.

TANG Jian-zheng. Present status and future prospects of vacuum glass industry[J]. Glass, 2008, 203(8): 26−36.

[2]张瑞宏, 马承伟, 张俊芳. 真空玻璃技术在温室工程中的应用分析[J]. 农机化研究, 2005, 28(3): 188−191.

ZHANG Rei-hong, MA Cheng-wei, ZHANG Jun-fang. Analysis of vacuum plate glass technique using in greenhouse engineering[J]. Journal of Agricultural Mechanization Research,2005, 28(3): 188-191.

[3]龙文志.新型节能幕墙: 真空玻璃幕墙[J]. 建设科技, 2005,20(5): 8−10.

LONG Wen-Zhi. A new energy-saving curtain wall: vacuum glass curtain wall[J]Construction Science and Technology, 2005,20(5): 8−10.

[4]Ng N, Collins R E, So L. Characterization of the thermal insulating properties of vacuum glazing[J]. Materials Science and Engineering (B), 2007, 138(2): 128−134.

[5]Ng N, Collins R E, So L. Thermal conductance measurement on vacuum glazing[J]. International Journal of Heat and Mass Transfer, 2006, 49(25/26): 4877−4885.

[6]WANG J, EAMWS P C, ZHAO J F, et al. Stresses in vacuum glazing fabricated at low temperature[J]. Solar Energy Materi-als and Solar Cells, 2007, 91(4): 290−303.

[7]缪宏, 张瑞宏, 高建和. 真空玻璃传导和对流传热机理研究[J]. 玻璃, 2007, 191(2): 158−16.

MIAO Hong, ZHANG Rui-hong, GAO Jian-he. Study on the Mechanism of conductive and convective heat transfer in vacuum[J]. Glass, 2007, 191(2): 158−164.

[8]Timoshenko S, Krieger S W. Theory of plates and shells[M].New York: McGraw-Hill Book Co, 1977: 22−23.

[9]张瑞宏, 顾乡, 张华. 真空玻璃应力支撑实验研究[J]. 真空科学与技术学报, 2006, 26(2): 455−458.

ZHANG Rei-hong, GU Xiang, ZHANG Hua. Experimental study on the braced stress of the vacuum glazing[J]. Chinese Journal of Vacuum Science and Technology, 2006, 26(2):455−458.

[10]刘小根, 包亦望, 宋一乐, 等. 真空玻璃真空度在线检测技术与应用[J]. 郑州大学学报, 2009, 30(1): 101−105.

LIU Xiao-gen, BAO Yi-wang, SONG Yi-le, et al. Research on online measuring technique and application for vacuum degree of the vacuum glass[J]. Journal of Zhengzhou University:Engineering Science, 2009, 30(1): 101−105.

[11]Lawn B R. Fracture of brittle solid[M]. 2nd ed. Cambridge:Cambridge University Press, 1993: 156−160.

[12]马眷荣, 罗忆, 刘忠伟. 建筑玻璃应用技术[M]. 北京: 化学工业出版社, 2004: 206.

MA Juan-rong, LUO Yi, LIU Zhong-wei. Technology of building glass application[M]. Beijing: Chemical Industry Press,2004: 206.

[13]Fischer-Cripps A C, Collins R E. Architectural glazings: design standards and failure models[J]. Building and Environment,1995, 30(1): 29−40.

[14]龙文志. 玻璃结构与结构玻璃[C]//2008年中国玻璃行业年会暨技术研讨会论文集. 北京, 2008: 332−365.

LONG Wen-zhi. Glass structure and structure glass[C]//Collection of Technical Seminar for 2008 Chinese Glass Profession Annual Meeting. Beijing, 2008: 332−365.

[15]Ventsel E, Krauthammer T. Thin plates and shells-theory analysis and applications[M]. New York: Marcel Dekker, 2001:57−58.

(编辑 张曾荣)

Bearing behavior and strength design for building vacuum glazing

LIU Xiao-gen1, BAO Yi-wang1, WAN De-tian1, QIU Yan1, WANG Xiu-fang1, XU Hai-feng2

(1. China Building Material Academy C＆T Central, Key State Laboratory of Green Building Materials, Beijing 100024, China;2. Beijing Synergy Vacuum Glazing Technology Company, Beijing 101111, China)

The strength behavior of the vacuum glazing and influencing factors were investigated by using uniform load test on the glass plate. Based on the test results and stresses distribution characteristics in vacuum glazing, and considering the influence of the additional supporting stress, the calculation formula of resistance to wind load and strength design factors of the glass under preexisting tension stress function were given. The results show that the deformation of the outer and inner panel of the vacuum glass is identical, and the load distribution on the two glass panels are proportional to the stiffness of the glass panel. For a given total thickness of the two glass panels, the strength reaches the highest when both glass panels have the identical thickness. The capacity of resisting wind load of the vacuum glazing is the same as a common glass whose thickness is about 85% of the total thickness of the vacuum glazing. The preexisting tension stress in the outer-side surface of the vacuum glazing, which affects the strength of the vacuum glazing, should be taken into account in strength design. The maximum stress in the vacuum glazing is at the centre of the glass plate under uniform load.

vacuum glazing; bearing behavior; supporting stress; lasting stress; strength design

中文分类号：TU502

A

1672−7207(2011)02−0349−07

2009−12−10；

2010−02−15

国家自然科学基金资助项目(50672093，50772103)；北京市自然科学基金资助项目(2082026)；北京市科委项目(D08050303450803)；国家高技术研究发展计划(“863”计划)项目(2007AA03Z526)

刘小根(1976−)，男，江西永丰人，博士研究生，从事无机非金属材料性能表征与评价研究；电话：010-51167945；E-mail：xtlxg88@163.com