基于反应基元的非线性系统灰箱建模方法

曹柳林，孙娅苹，吴海燕

(北京化工大学 自动化研究所，北京，100029)

基于反应基元的非线性系统灰箱建模方法

曹柳林，孙娅苹，吴海燕

(北京化工大学 自动化研究所，北京，100029)

提出一种基于反应基元的建立复杂非线性系统模型的灰箱建模方法。首先根据先验知识及系统特性分析引入过程的初始反应基元，并以此为出发点建立结构逼近神经网络模型，实现基元之间的关联，赋予网络节点实际的物理意义；然后，通过提出的最小化预测误差，结合逐步回归分析方法选择最优反应基元，优化网络结构，建立起表示系统变量关系的灰箱模型。以实际橡胶硫化促进剂制备的间歇反应过程作为实验对象，建立以生成物浓度为输出的数学模型，达到较高的输出预测精度。

灰箱建模；非线性系统；系统辨识；间歇反应；结构逼近神经网络

在对复杂间歇化工过程建模时，由于系统的非线性、非稳态、过程变量的约束以及有限的在线测量信息等因素的限制，很难对系统进行“白箱”描述，因此，建立纯粹的机理模型难度很大；而黑箱建模方法单纯利用系统输入输出数据的拟合，没有充分利用先验知识，泛化精度往往难以达到实际的生产要求。因此，融合2种建模方法、充分利用系统的先验知识的灰箱建模方法是系统建模发展的趋势和研究热点[1−6]。近年来，针对复杂的化工过程，常常使用机理模型[1−14]与神经网络方法相结合的混合建模方法。根据机理模型与神经网络的相对位置，主要采用以下2种方式：在串联型模型[9−11,14]中，利用机理模型构成整体模型的框架，神经网络则拟合那些不易确定的反应动力学参数；在并联模型[4−6]中，神经网络针对机理模型的误差对模型进行补偿。在此，本文作者提出一种基于反应基元(Fundamental genes)的灰箱建模方法，它是基于以下事实：大多数反应过程遵循的基本规律是大致知晓的，但先验知识不足以具体描述出系统模型的结构。本文作者通过分析这些先验知识，从中挑选出最能反映系统特性的函数单元(称作反应基元)，并通过结构逼近神经网络建立各反应基元之间的关联关系，以此建立系统的数学模型。

1 橡胶硫化促进剂制备的间歇缩合反应

在实验装置内进行的橡胶硫化促进剂的制备是一个间歇缩合反应，其原理图如图1所示。反应包括原料计量和缩合工序2个阶段。此间歇缩合反应是由原料邻硝基氯苯(C6H4CINO2)、硫化钠(Na2S)及二硫化碳(CS2)在反应釜中经夹套蒸汽加入适度的热量后，发生复杂的化学反应，产生橡胶硫化促进剂的钠盐及其副产物。用 A，B和 C分别代表原料邻硝基氯苯(C6H4CINO2)、硫化钠(Na2S)及二硫化碳(CS2)，D和E分别代表橡胶硫化促进剂及其副产物。在每次操作中，原料经计量后，一次投料，在反应釜中发生缩合反应，反应包括加热升温、冷却控制和保温等阶段，反应完成后，进行出料和清釜等操作[15]。图1中各变量定义如下：cA，cB，cC和cC分别表示A，B，C和D的浓度；T为反应温度；Tx为夹套温度；k1和k2分别为主、副反应速率常数；R1和R2为主、副反应速率；F为夹套冷却水入口流量。反应器中发生如下反应：

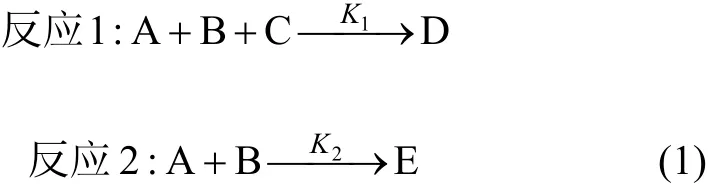
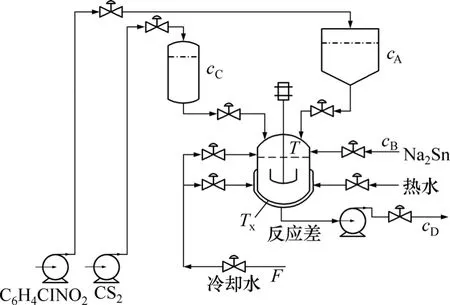
图1 橡胶硫化促进剂制备过程Fig.1 Producing accelerant for sulfuring rubber

在此缩合反应中，化学反应复杂，除了原料A，B和C发生的主反应外，还有原料A和B发生的副反应，且缩合反应收率与副反应有密切的关系。当主反应的活化能高于副反应的活化能时，提高反应温度有利于主反应的进行。但此间歇反应是一个放热反应，升温过快、过高，容易爆炸而产生危险。

2 建立基于反应基元的间歇反应器的灰箱模型

反应基元是描述系统各部分特性的系统变量的函数单元。通过反应基元的引入，将系统各部分特性函数化，使建模过程灰箱化。

建模过程分三部分进行：首先根据系统先验知识和特性分析提取系统的简单函数项(如：反应速率采用exp(x;c)，系统的阻尼振荡特性采用 sin(x;c)，其中x是系统的状态变量，c是对应参数[5])，利用简单函数项及组合函数构建候选的反应基元池；其次，从候选池中选择最基本和最重要的变量和函数作为初始的反应基元，以此构成神经网络的节点，确立神经网络模型结构；随后，使用逐步回归分析方法，依次从候选基元池中挑选基元加入网络，以最小化预测模型误差为性能指标，优化网络结构，提取最优反应基元，最终建立系统输入输出关系的模型。这种灰箱建模方法赋予网络节点实际的物理意义，使系统的先验知识被分布描述于网络中，因此，被称为结构逼近神经网络(Structure approaching neural network, SANN)。提取系统的反应基元和选择合适的参数估计方法实现反应基元间的关联是灰箱建模方法的关键和难点。

2.1 建立候选反应基元池

从对化工过程的机理分析中可以获取系统的某些先验知识，但这些先验知识常常无法适合系统建模的具体表达(如反应速率和系统阻尼振荡特性等)。这里通过机理分析和经验公式提取对系统特性描述相关的反应基元，并将反应基元以基本的函数形式表示。

通过对间歇反应过程的分析，可知先验知识包括：此反应为放热反应，k1和k2满足阿累尼乌斯方程，即它们 是1/T的指数函数形式；反应物和生成物浓度随时间的变化速率由反应速率R1和R2的函数关系表达，而R1和R2是k1，k2及cA，cB和cC的函数；对此间歇反应过程，反应温度T是影响cD的最主要因素，可通过控制夹套温度Tx确保反应温度在所需的范围内。在本实验对象中，利用调节冷却水流量F从夹套内移出热量来控制Tx。因此，考虑到控制目标，要建立的模型是以控制量F为输入，以被控目标cD为输出。

根据上述机理分析，可进行简单函数项的提取：

(3) 考虑系统的动态特性，k时刻的系统输出cD(k)与其历史状态cD(k−i)有关，本文中最大时延项i取5；

(4) 考虑到间歇反应的复杂性及外界干扰的影响，反应温度会具有一定程度的阻尼振荡，因此，增加简单函数项sinT；

(5) 由方程(1)得知，组分A和B的浓度具有相同的变化速率，反应速率R与它们的乘积有关，因此，增加项而不再考虑cB；

(6) 考虑反应温度T与输出cD的非线性关系，将T2作为一简单函数项。

由于各变量及简单项之间可能存在着交叉、耦合关系，为避免疏漏，逐次将任意2个简单项相乘生成组合函数项。

在上述选择反应基元的过程中，生成简单函数和组合函数总计78项放入候选反应基元池中，并从中优选出T，F，cA，cAF以及cD(k−1)作为初始反应基元。

2.2 建立结构逼近神经网络(SANN)

反应基元可被分为2类：一是基本的自主变量T，F和cA；二是由基本变量构成的函数，分别称为基本变量基元和基本函数基元。

将基本变量基元作为神经网络第一隐含层的节点，建立基本变量层FVL，将基本函数基元作为网络第二隐含层的节点，建立基本函数层FFL，每层输出都作为网络输出层的输入，模型前几个时刻的输出回馈作为系统的内部输入，d表示输出延迟的步长，w0表示网络输出层的阈值，网络整体结构如图2所示。由于神经网络节点由反应基元构成，从而使系统的先验知识被分布描述于网络中，因此，该网络被称为结构逼近神经网络。为描述方便，以下以y表示对象输出，ym表示模型输出(输出变量cD)，u表示输入变量(F)。

2.3 优化网络结构建立间歇反应器的灰箱模型

结构逼近神经网络结构见图 2。其中，输出变量ym(k)可被下式近似表示：

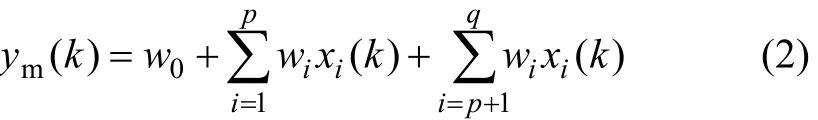
式中：wi为网络隐含层与输出层之间的权值；xi(k)表示各最优反应基元(所选定的输出y的各历史状态y(k−j)也作为最优变量基元，采用xi(k)表示，j=1, 2, …,d)；p为最优变量基元个数；q−p为函数基元个数(q≥p)，q为总反应基元个数。

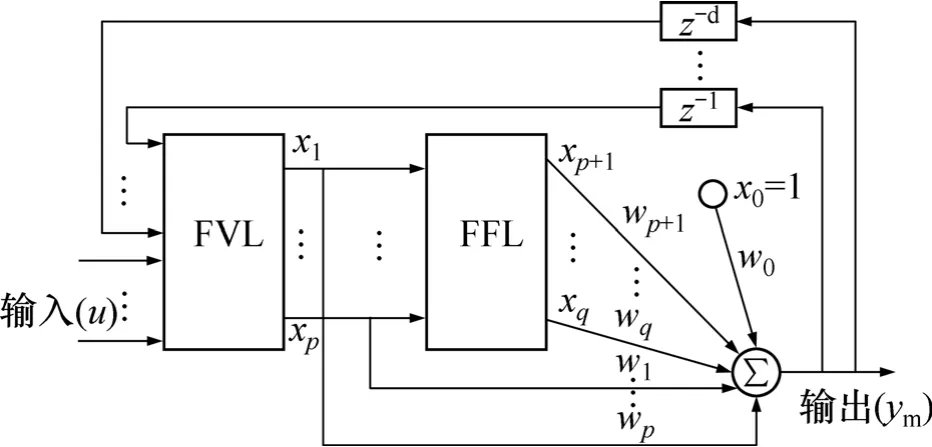
图2 结构逼近神经网络结构图Fig.2 Architecture of SANN

式中：Wq为具有q项最优反应基元的神经网络的隐含层与输出层之间的权值；q=p，p+1，…。

采用逐步回归分析方法选择最优反应基元：

(1) 初始化。在图 2所示的神经网络中，选择如上所述的5项初始反应基元放入最优反应基元池中，即q=5，以最优反应基元作为网络的隐含层节点，建立图2所示的神经网络，利用递推最小二乘算法进行网络训练，并计算初始Jq。将这些初始基元从候选的反应基元池中剔除，更新候选反应基元为78−q=7 373项。为候选反应基元进入最优反应基元池设定需要满足的最小损失性能指标δJ。

(2) 设q=q+1，训练网络并计算ΔJqj(j=1，2，…，78−q)。从候选反应基元池中依次选出每个反应基元，分别与最优反应基元池中的基元共同作为网络的隐含层节点，分别建立图2所示的神经网络，利用递推最小二乘算法进行网络训练，并计算相应的ΔJqj。

(3) 最优反应基元的选择。在得到的上述ΔJqj中，选择最小值，记作minΔJq，且当ΔJqj≤δJ时，对应的xq+1即为第q+1项最优反应基元；否则结束选择。

(4) 更新。将xq+1增加到最优反应基元池，并将其从候选反应基元池中删除，转到(2)，直至结束。

通过上述选择过程，找到了反映系统特性的最优反应基元，确定了神经网络结构和隐含层节点数目，同时避免了系统变量的冗余，达到优化网络结构、实现反应基元关联的目标。

在对图1所示的实验装置建模时，以5 s为采样时间，连续采样 250 min，在不同的操作条件下多次采样，作为训练数据。其中，最小损失性能指标 δE设定为0.05。

经过训练，找到反映系统特性的最优反应基元共12项，即在建立的神经网络模型中，2个隐含层共包含12个节点，分别为

3 模型验证

以5 s为采样时间，对图1所示的实验装置连续采样250 min，作为泛化数据，进行模型验证。

定义模型预测性能指标：

式中：e(i)是模型输出ym与系统输出y在第i时刻的绝对误差。验证分为2种情况进行。

第1种情况：ym(k)=f(y(k−i)，u(k))，利用系统输出的历史数据y(k−i)自反馈作为模型的输入。

第2种情况：ym(k)=f(ym(k−i)，u(k))，利用模型输出的历史数据ym(k−i)自反馈作为模型的输入，它对应许多产品浓度的测量存在严重滞后或不可在线测量的情况。

在第1种情况下得到的泛化曲线和泛化误差曲线分别见图 3和图 4，采用式(7)得到的泛化指标为0.058%。第2种情况下的泛化曲线和泛化误差分别见图5和图6，泛化指标为2.36%。

为更好地进行模型验证，本文建立了以F和cA作为输入变量，cD和T作为输出变量的B样条神经网络和对角递归神经网络构成的并联神经网络模型。仿真结果见表1。

由泛化结果知：采用反应基元的灰箱建模方法，间歇反应器的输出预测精度较高。

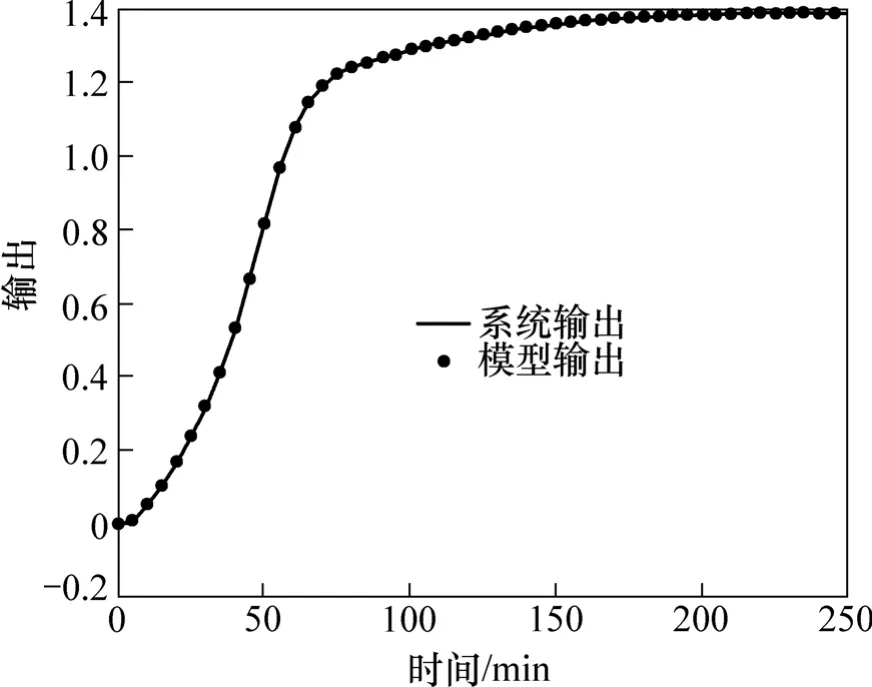
图3 情况1的泛化曲线Fig.3 Test result in the 1st case

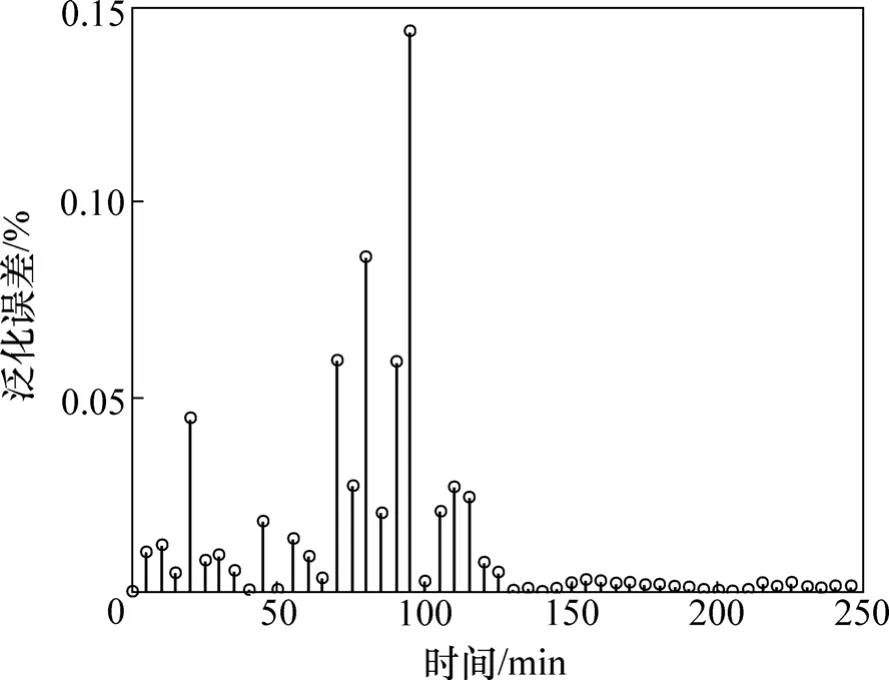
图4 情况1的泛化误差Fig.4 Test error in the 1st case

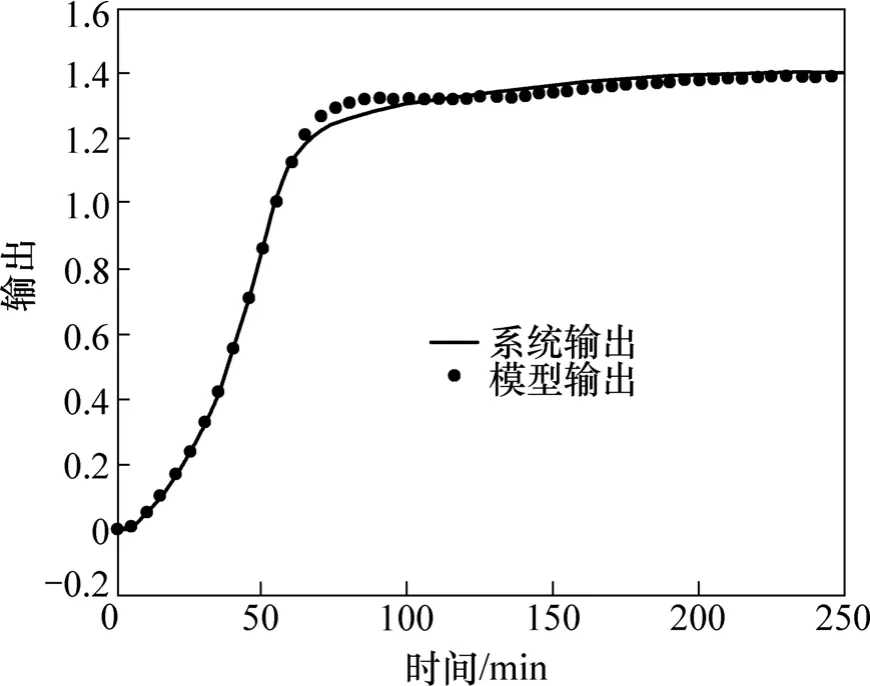
图5 情况2的泛化曲线Fig.5 Test result in the 2nd case

图6 情况2的泛化误差Fig.6 Test error in the 2nd case

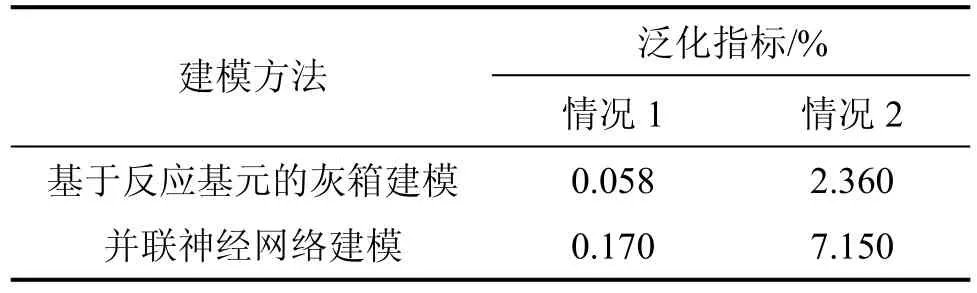
表1 2种方法仿真结果对比Table 1 Results of two methods

4 结论

(1) 提出基于反应基元的灰箱建模方法。该方法能够在先验知识不足、不能明确描述系统模型结构的情况下建立系统模型，并达到较高精度。

(2) 引入描述系统各部分特性的反应基元，充分挖掘和利用了有限的系统先验知识。

(3) 采用反应基元作为节点建立结构逼近神经网络，使网络节点具有物理意义，可实现网络结构的合理化。

(4) 采用逐步回归分析方法选择最优反应基元，优化网络结构，避免冗余，提高模型预测精度。

[1]曹柳林, 李晓光, 王晶. 利用结构逼近式混合神经网络实现间歇反应器的建模[J]. 化工学报, 2008, 59(4): 958−963.

CAO Liu-lin, LI Xiao-guang, WANG Jing. Modeling of batch reactor based on structure approaching hybrid neural networks approach[J]. Journal of Chemical Industry and Engineering(China), 2008, 59(4): 958−963.

[2]李晓光, 江沛, 曹柳林, 等. 状态变量部分不可测的间歇反应器的智能建模[J]. 化工学报, 2008, 59(7): 1818−1823.

LI Xiao-guang, JIANG Pei, CAO Liu-lin, et al. Intelligent modeling of batch reactor with partially unmeasurable states[J].Journal of Chemical Industry and Engineering (China), 2008,59(7): 1818−1823.

[3]QIANG Xiong, Arthur J. Grey-box modeling and control of chemical processes[J]. Chemical Engineering Science, 2002, 57:1027−1039.

[4]McAfee M. Enhancing process insighting in polymer extrusion by grey box modeling[J]. Transactions of the Institute of Measurement and Control, 2007, 29(5): 467−488.

[5]Reinout R, Leyla K, Weiland S, et al. A grey-box modeling approach for the reduction of nonlinear systems[J]. Journal of Process Control, 2008, 3(18): 906−914.

[6]Sohlberg B. Hybrid grey box modeling of a pickling process[J].Control Engineering Practice, 2005, 13: 1093−1102.

[7]高春华, 王慧, 李平. 混合系统建模、分析与综合: 研究进展与展望[J]. 系统工程理论与实践, 2002, 22(11): 15−20.

GAO Chun-hua, WANG Hui, LI Ping. Modeling, analysis and synthesis of hybrid systems: A review[J]. System Engineeringtheory & Practice, 2002, 22(11): 15−20.

[8]王景杨, 苑明哲, 曹景兴, 等. 基于最小二乘参数辨识的非线性机理模型研究[J]. 沈阳理工大学学报, 2008, 27(3): 47−51.

WANG Jing-yang, YUAN Ming-zhe, CAO Jing-xing, et al. A study on the non-linear mechanism model based on parameters identification by least square model[J]. Transactions of Shenyang Ligong University, 2008, 27(3): 47−51.

[9]吴燕玲, 卢建刚. 基于遗传规划和过程机理的混合建模方法[J]. 自动化与仪表, 2008, 23(6): 5−8.

WU Yan-ling, LU Jian-gang. Hybrid modeling based on genetic programming and mechanism knowledge[J]. Automation &Instrumentation, 2008, 23(6): 5−8.

[10]邵雷, 雷虎民, 刘代军, 等. 基于微粒群算法的非线性系统建模方法研究[J]. 控制与决策, 2009, 24(1): 21−25.

SHAO Lei, LEI Hu-min, LIU Dai-jun, et al. Study of nonlinear system modeling based on particle swarm optimizer[J]. Control and Decision, 2009, 24(1): 21−25.

[11]Ng C W, Hussain M A. Hybrid neural network-prior knowledge model in temperature control of a semi-batch polymerization process[J]. Chemical Engineering and Processing, 2004, 43:559−570.

[12]Hinchliffe M, Montague G, Willis M. Hybrid approach to modeling an industrial polyethylene process[J]. AICHE J, 2003,49(12): 3127−3137.

[13]Doyle F J, Harrison C A, Crowley T J. Hybrid model-based approach to batch-to-batch control of particle size distribution in emulsion polymerization[J]. Computers and Chemical Engineering, 2003, 27: 1153−1163.

[14]杨慧中, 张素贞, 陶振麟. 聚合反应过程质量指标的推理估计混合模型[J]. 高校化学工程学报, 2003, 17(5): 552−558.

YANG Hui-zhong, ZHANG Su-zhen, TAO Zhen-lin. A hybrid model for inference estimation of the performance figure in polymerization process[J]. Journal of Chemical Engineering of Chinese Universities, 2003, 17(5): 552−558.

[15]吴重光. 过程控制技能测试[M]. 北京: 化学工业出版社,2006: 1−22.

WU Chong-guang. Process control skill test[M]. Beijing:Chemical Industry Press, 2006: 1−22.

(编辑 杨幼平)

Grey-box modeling based on fundamental genes for nonlinear system

CAO Liu-lin, SUN Ya-ping, WU Hai-yan

(Institute of Automation, Beijing University of Chemical Technology, Beijing 100029, China)

An approach of grey-box modeling based on fundamental genes was developed for modeling dynamic processes with non-linear characteristics. By combination the prior knowledge and systematic behaviors, structure approaching neural network (SANN) was established based on fundamental genes, and the nodes of SANN were given actual significance. Then the optimal fundamental genes were chosen through minimizing the proposed predicted error with stepwise regression analysis (SRA) to optimize the structure of SANN, so as to get the grey-box model. Detailed process of modeling was described in modeling of batch condensation reaction of producing promoter for vulcanizing rubber. The simulation result proves that the approach is effective.

grey-box modeling; nonlinear system; system identification; batch reaction; structure approaching neural network

TQ 316.37

A

1672−7207(2011)02−0414−05

2010−02−02；

2010−04−25

国家自然科学基金资助项目(60704011, 60974031)

曹柳林(1951−)，女，山西临汾人，教授，博士生导师，从事聚合反应过程的微观建模与控制、神经网络建模与控制、自适应控制与先进控制等方向的研究；电话：010-64434930；E-mail：caoll@mail.buct.edu.cn