冷绕成形螺旋弹簧回弹理论及数值模拟

王时龙，雷松，周杰，萧红，杨勇，冯治恒

(重庆大学 机械传动国家重点实验室，重庆，400030)

冷绕成形螺旋弹簧回弹理论及数值模拟

王时龙，雷松，周杰，萧红，杨勇，冯治恒

(重庆大学 机械传动国家重点实验室，重庆，400030)

针对现有研究未考虑张力对螺旋弹簧成形及回弹影响的问题，建立受张力影响的螺旋弹簧成形及回弹理论；讨论当簧丝受弯矩和张力共同作用时，弯矩与簧丝横截面应力、张力与簧丝横截面应力、回弹比与张力的关系；通过大型非线性有限元分析软件ABAQUS 6.8实现不同张力下螺旋弹簧冷绕成形过程的数值模拟。理论计算与模拟结果均表明：张力不同会导致弹簧最终回弹量的不同；张力越大，簧丝在卸载时越容易保持成形时的形状，回弹量越小；实际生产弹簧时，在除张力外的其他参数不易改变的情况下，可通过增大或减小张力的方法来减小或增大回弹量。

螺旋弹簧；簧丝；成形；回弹理论；张力；数值模拟

螺旋弹簧冷绕绕制成形时，簧丝要承受较大的弹塑性弯曲，卸载后其弹性部分要恢复，因此，缠绕后存在着回弹问题[1]。回弹一直是制约弹簧生产质量、成本，并限制生产效率的关键因素之一，是工程界未能有效解决的技术难题。殷仁龙等[1−3]从圆截面梁的弹塑性纯弯曲理论出发，研究了弯曲时簧丝横截面内的应力与应变、弯矩与簧圈曲率的关系[4]。但是，弹簧冷绕成形是一种蕴含簧丝拉伸、弯曲和扭转的复合变形过程，是一个包含几何非线性、材料非线性、接触非线性的强非线性问题；因此，仅仅把弹簧冷绕成形考虑成弹塑性纯弯曲过程存在局限性。Bibel等[5]认为张力使回弹的减小是因为张力会使簧丝横截面中性轴发生偏移，但张力只作用于中性轴以内簧丝横截面区域，弯矩只作用于中性轴以外簧丝横截面区域，显然这不符合实际簧丝横截面应力分布情况。在此，本文作者建立了考虑张力影响的螺旋弹簧成形及回弹理论，进一步分析了张力对弹簧回弹的影响。目前关于板材冲压回弹及管材弯曲回弹的数值模拟较多见[6−9]，而对于螺旋弹簧冷绕成形及回弹的数值模拟还未见文献报道。因此，本文作者还进行了不同张力下螺旋弹簧冷绕成形过程的有限元数值模拟。

1 受张力影响的螺旋弹簧回弹理论

螺旋弹簧冷绕成形过程如图1所示，簧丝由卡盘固定，在主轴旋转的同时，簧丝进给装置在床身轴向左、右移动，将簧丝绕在芯轴上卷制成弹簧。该过程可等效为长为l、半径为r的簧丝受到1对弯矩M和1对张力N的共同作用，见图2。当簧丝承受的弯矩M和张力N较小时，簧丝完全为弹性变形，横截面上应力按直线分布，边缘(r=d/2，d为簧丝直径)上的应力为：

式中：σM为因弯矩产生的应力；σN为因张力产生的应力；σ为合应力。

当弯矩M=Ms，张力N=Ns时，簧丝边缘处的应力刚好达到初始屈服应力σs，于是，有：

移动应用开发技术栈主要是框架和组件库的选型，架构师的主要工作已从原来的实现技术框架(加法)转变为从海量技术中选择最合适的技术组件(减法)。企业的移动开发团队需对移动应用的类型和技术领域进行分析，结合团队自身的技术积累和可能的投入总结出一套应对移动开发模式的技术栈。图1为移动开发技术栈参考模型，针对不同类型的开发模式，给出相应的技术选择域，对技术团队建设具有指导意义。

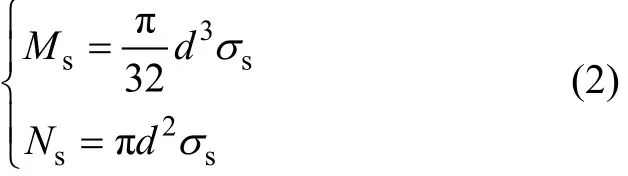
因此，只要得到了无量纲回弹比η和张力无量纲量n的关系，就能说明张力对弹簧最终回弹的影响。考虑到b＜r且c+b＜r，即q＜1且p+q＜1，由式(9)和(11)可得到η和n的关系，结果如图4所示。

各地可疑者调查范围不尽相同,有以全人口或15岁以上人口为调查对象。一般有可疑症状者的报告率控制在5%~10%,则可缩小检查对象90%~95%;检出病人占实有现患的比率可提高到80%~90%,其中以有可疑症状和有既往史者发现率为高[8,9]。

冷绕弹簧时，簧丝受到的弯矩远大于Ms，在簧丝横截面上沿弹簧圈半径方向的内外表层纤维将产生塑性变形，并且随着力矩的增大，塑性变形还要向簧丝内层延伸。与圆截面梁的纯弯曲理论相比，弯矩和张力共同作用时簧丝的中性轴会偏离截面几何中心，见图3。在图3中：c为初始屈服纤维到中性轴的距离；b为中性轴到截面几何中心的距离。本文考虑簧丝材料为弹−线性强化材料，设z为簧丝横截面上任意一点到截面几何中心的距离，则弯矩和张力共同作用时簧丝横截面的应力为：

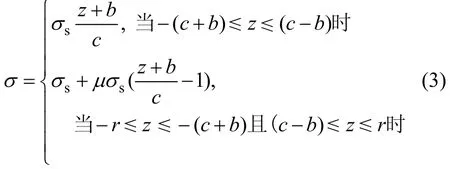
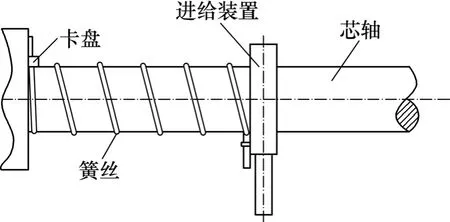
图1 螺旋弹簧冷绕成形过程Fig.1 Cold-coiling process of helical springs

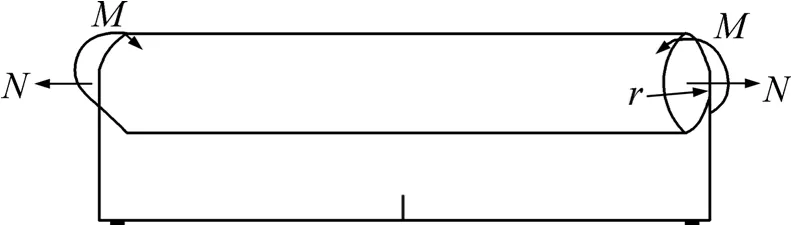
图2 簧丝受1对弯矩M和1对张力N的共同作用Fig.2 Applying bending moment and tensile force to spring wire together

图3 簧丝圆形横截面上沿厚度方向的应力分布Fig.3 Stress distributions within cross-section of spring wires along thickness

1.1一般资料2016年1月至9月我院对92例短暂性脑缺血患者进行了研究分析,共有62例男性和30例女性,最小41岁,最大76岁,平均(67.3±2.9)岁;将患者分成了对照组和研究组,均有46例患者。

为了使公式简洁，引入弯矩无量纲量m与张力无量纲量n[10−12]：

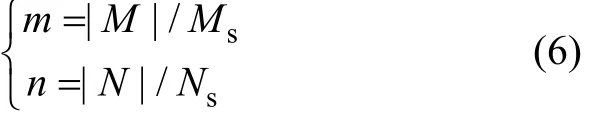
为了说明张力对弹簧回弹的影响，需求得弹簧回弹后的曲率或回弹比。由于圆截面梁在弹塑性弯曲后卸载不会引起纤维的反向屈服，因此，卸除M和N相当于叠加−M和−N引起的纯弹性效应。轴力的纯弹性效应将不改变曲率，因而回弹后簧丝的曲率为：

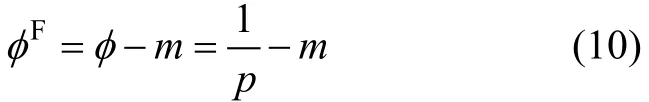
式中：Fφ为回弹后的无量纲曲率；为回弹前的无量纲曲率[6]。

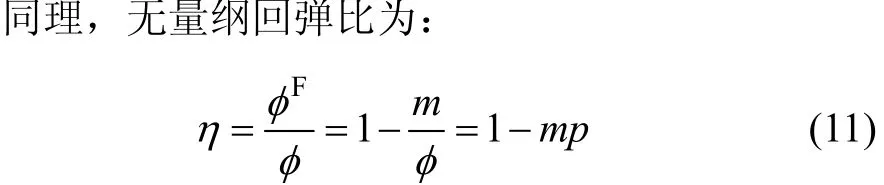
式中：Ms和Ns分别为簧丝边缘处的应力刚好达到初始屈服应力时的弯矩和张力。

对此，张凯深有感触，“我记得过去不管穿什么样的衣服，晚上到家都是油乎乎的。现在我们穿着白衬衣晚上回家依旧是白的。很多事情中国石油加油员都帮我们做了。”

式中：A为簧丝横截面的面积。

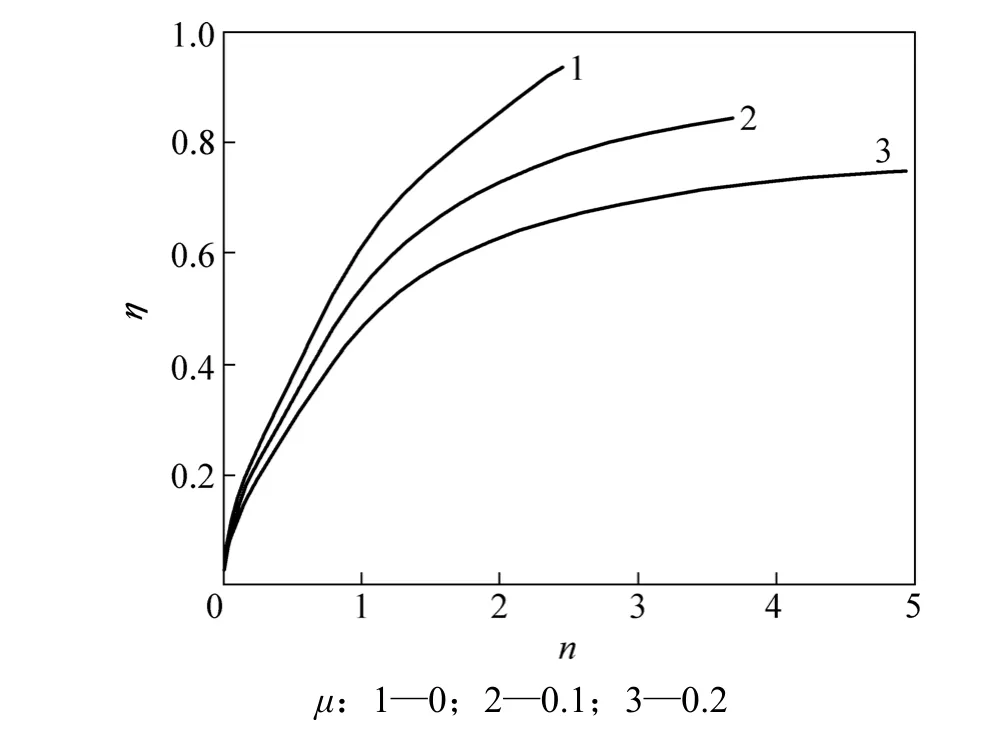
图4 μ不同时无量纲回弹比η与张力无量纲量n的关系Fig.4 Relationships between dimensional springback ratioAnd tensile force under different μ

通过进一步分析可以得到：在弹簧成形过程中，除张力变化而其余参数一定的情况下，张力不同会导致弹簧最终回弹量不同，即弹簧回弹后的尺寸、精度和质量不同。由于文献[1−3]中在没有考虑张力的情况下研究弹簧成形后的回弹，因此，其结果是有局限的。同时，冷拉碳素簧丝绕制弹簧时，在其他参数不变的情况下，可通过增大或减小张力来减小或增大最终弹簧的回弹量，以提高弹簧回弹后的精度和质量。

2 数值模拟计算

2.1 计算模型

当弹簧成形时，簧丝外侧受拉伸，内侧受压缩，并且簧丝中性轴会向下偏移。应力沿簧丝横截面的分布如图3所示。为了真实地反映弹簧绕制过程中簧丝横截面应力的分布，本文作者采用三维实体单元对簧丝建模。螺旋弹簧冷绕成形的有限元计算模型如图 5所示。

由图4可见：随着张力的增大，回弹比η增大；在初始张力增大不多的情况下，回弹比急剧增大，即η/n较大；随着张力的继续增大，回弹比增大不多，η/n增大趋势逐渐趋于平缓；回弹比越大，使簧丝在卸载的过程中能够较好地保持成形时的形状，即回弹量减小。

为了进一步说明弹簧成形过程中张力的影响，本文作者采用ABAQUS 6.8中的ABAQUS/ Explicit模块，并用准静态分析的方法模拟弹簧冷绕成形过程。根据图1所示的弹簧冷绕成形原理，采用三维模型建立簧丝、芯轴、套筒和卡盘等部件。由于芯轴、套筒和卡盘的刚度远远大于簧丝的刚度，并且其本身的应力和变形不是所关心的对象，因此，采用三维离散刚体部件对芯轴和卡盘建模(芯轴与卡盘合并在一起后呈不规则形状，因此，应采用三维离散刚体部件建模)；采用三维解析刚体部件对套筒建模。在分析过程中，刚体部件不参与所有基于单元的计算，因而可以节约大量的时间。另外，在接触分析中，如果接触对的主面是刚体部件的面，分析时结果就更容易收敛。

（2）给工程质量带来极大隐患。建设单位与施工单位之间相互制约的关系，被个人或小集体经济利益所取代，使得双方对工程质量与安全的责任约束降到了极限，偷工减料，不执行工程建设强制性标准等行为，给工程埋下结构安全和质量隐患。

图5 螺旋弹簧冷绕成形有限元计算模型Fig.5 FEM computing model of cold-coiling process of helical springs

套筒为解析刚体部件，不需要划分网格；芯轴和卡盘为离散刚体部件，选用R3D4单元进行简单网格划分即可。弹簧冷绕成形是一个大变形的复杂接触问题，因此，应使用 C3