准一维H型结波导功分器研究

王文智 金荣洪 耿军平 梁仙灵

(教育部高速电子系统设计与电磁兼容研究重点实验室，上海交通大学，上海 200240)

1. 引 言

金属波导功分器具有低插入损耗的优点，常用于天线阵列馈电网络及雷达系统馈源的设计[1-2]。若采用传统形式的波导功分器，如T型结、Y型结及波导电桥等，在构造波导功分网络时整体结构需要向两维甚至三维的方向进行伸展[1，3]，严重制约大型阵列在车载、机载等对紧凑性要求较高的场合中的应用。已有不少学者对此问题进行研究并提出了一些解决方案，如采用基片集成波导技术[4-5]、径向功率分配/合成器[6-7]、新型馈电方式[8]等。尽管如此，这些方案在损耗、空间布局、设计难度等方面仍受到一定的限制。为此，本文提出一种新型的H型结波导功分器，在保持传统波导功分器各方面优点的同时，具有准一维的结构特征，适合于设计紧凑的波导功分网络，可为实际应用提供有价值的参考。

建立H型结的等效电路模型具有重要意义，是分析与设计的基础。然而，现有方法仍不能很好地提取H型结中有限壁厚耦合缝隙的等效电路参数，为模型的建立带来困难。为此，可根据文献[9]的等效方式，利用变分法对波导中有限壁厚耦合缝隙进行参数提取。变分法曾被用于分析零壁厚横向耦合缝隙的散射参数[10]，具有结果精确、形式简单等优点；但在有限壁厚的情况下，需要分别根据耦合缝隙上、下表面处的电场选取试函数，增加了求解的计算量。为此，可在变分法中引入平衡激励，在保证精度的前提下以单个试函数实现求解，使参数提取更为简单有效。

在H型结等效电路模型的基础上，可结合全波分析法对H型结进行设计。众所周知，等效电路法计算量小、物理意义明确，但模型的建立及元件参数的提取往往包含很多近似处理，仅据此进行设计精度必然会受到限制。相对而言，借助全波分析软件可以获得精确的结果，但需要耗费大量的计算时间。因此，可结合两者优点，首先利用H型结的等效电路模型快速获取接近较优解的设计参数，然后以此为基础进行全波分析及优化，最终完成设计。如此，可在时间与精度上取得折中，实现H型结快速、精确的混合设计方法。

2. H型结波导功分器

传统T型结由于分支波导垂直于主波导，用于波导功分网络设计时将占用庞大的空间。相对而言，H型结的波导分支互相平行且紧贴，具有紧凑的准一维结构，如图1(a)所示。其中，耦合缝隙用于电磁能量的合成或分配，附加的短路波导用于输入端口的匹配。此结构与字母H的形状相似，因此,称为H型结波导功分器。图1(a)所示为E面H型结，即从1端口处输入信号可在2、3端口处获得反相输出；同理可构造出H面H型结。

(a) 结构图

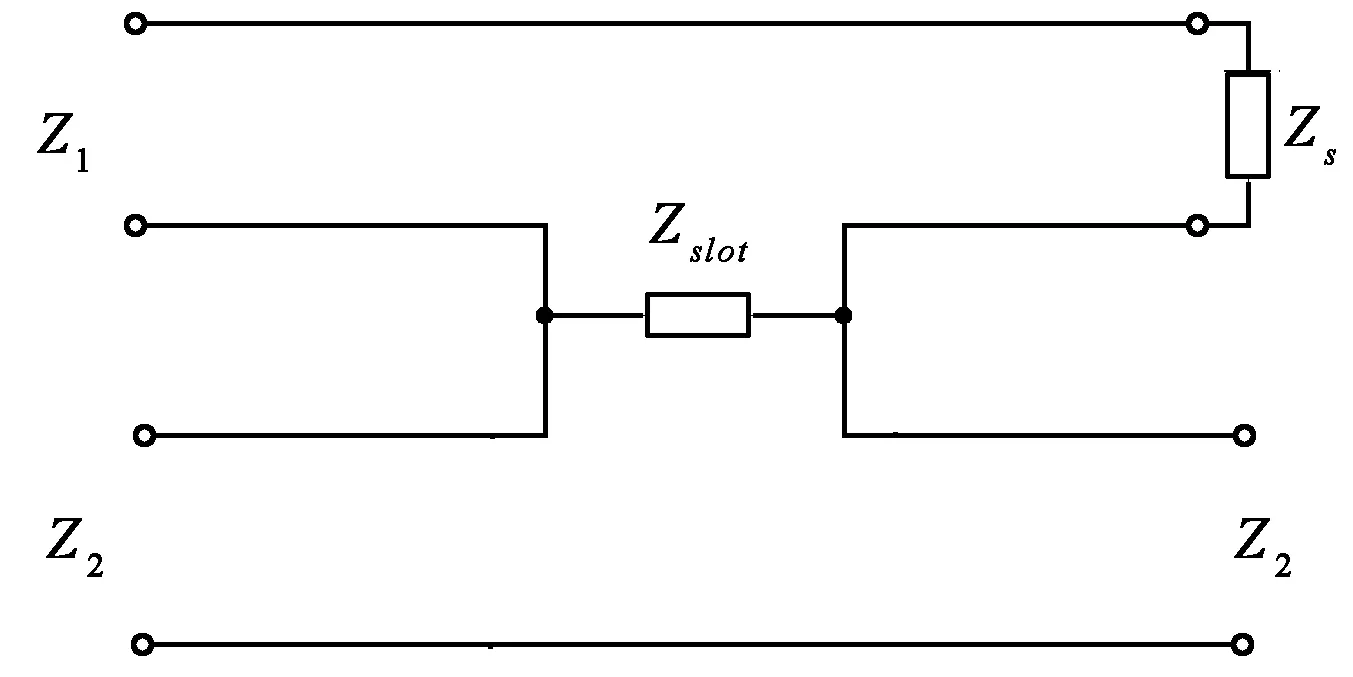
(b) 等效电路图1 E面H型结

根据相关论述[11-12]可得出H型结的等效电路，如图1(b)所示。其中，横向耦合缝隙导致波导沿纵向发生电压跃变，因此，等效为串联阻抗Zslot.Z1及Z2分别为上下两层波导的特征阻抗，Zs为短路波导的等效阻抗。由于H型结的等效电路中仅含有两个电抗元件，输入端反射系数一般仅存在单一零点，使阻抗带宽较窄。为此，可通过容性E面阶梯引入新的电抗元件，从而实现两个相邻零点以展宽带宽，如图2、图3所示。全波分析结果表明：增加E面阶梯后，一个典型H型结的 -20 dB相对带宽可达约10.7%，比之前的约3.4%提高超过两倍，如图4所示。除非特别指出，后续章节中的讨论均基于引入E面阶梯以后的H型结。此外，根据上述分析可以推测，若采用多缝耦合或多E面阶梯串联的结构，可能引入更多的相邻零点，从而实现更宽的阻抗匹配带宽。

(a) 结构图

(b) 等效电路图2 引入E面阶梯后的E面H型结

图4 E面阶梯对H型结的带宽展宽效果

3. 等效电路参数提取与混合设计方法

3.1 等效电路参数提取

H型结中的E面阶梯可等效为两个电容-jXC[12]，而它们之间的区域则可等效为两段特征阻抗为Z2、长度分别为l1与l2的传输线，如图2(b)所示。其中，Z3为2、3端口的特征阻抗。文献[12]已详细给出Zs和XC的闭合表达式，因此，只需再提取Zslot即可确定所有等效电路参数，进而为H型结建立起完整的等效电路模型。

当t>0时，可将耦合缝隙处划分为三个区域，如图5所示。参考文献[10]的方法，首先令一个归一化基模从某个端口处入射，并令两个区域分界面S1与S2上的入射电场与散射电场总和分别为ES1与ES2.随后，在S1与S2处放置理想电壁，并假设Si的两侧分别存在等效磁流±JMi=±ay×ESi,i= 1, 2。根据等效原理与格林函数法，可利用各区域的磁型并矢格林函数与相应的等效磁流获取不同区域中散射磁场的表达式。由总磁场的切向分量在区域分界面处连续的边界条件，联立由简正模法确立的散射系数表达式，可建立起入射端口反射系数关于ES1与ES2的变分表达式。按照精度要求，根据ES1与ES2的实际分布选取合理的试函数即可获得所需结果。最后，根据等效电路模型获得Zslot与反射系数的关系，即可提取出Zslot的闭合表达式。

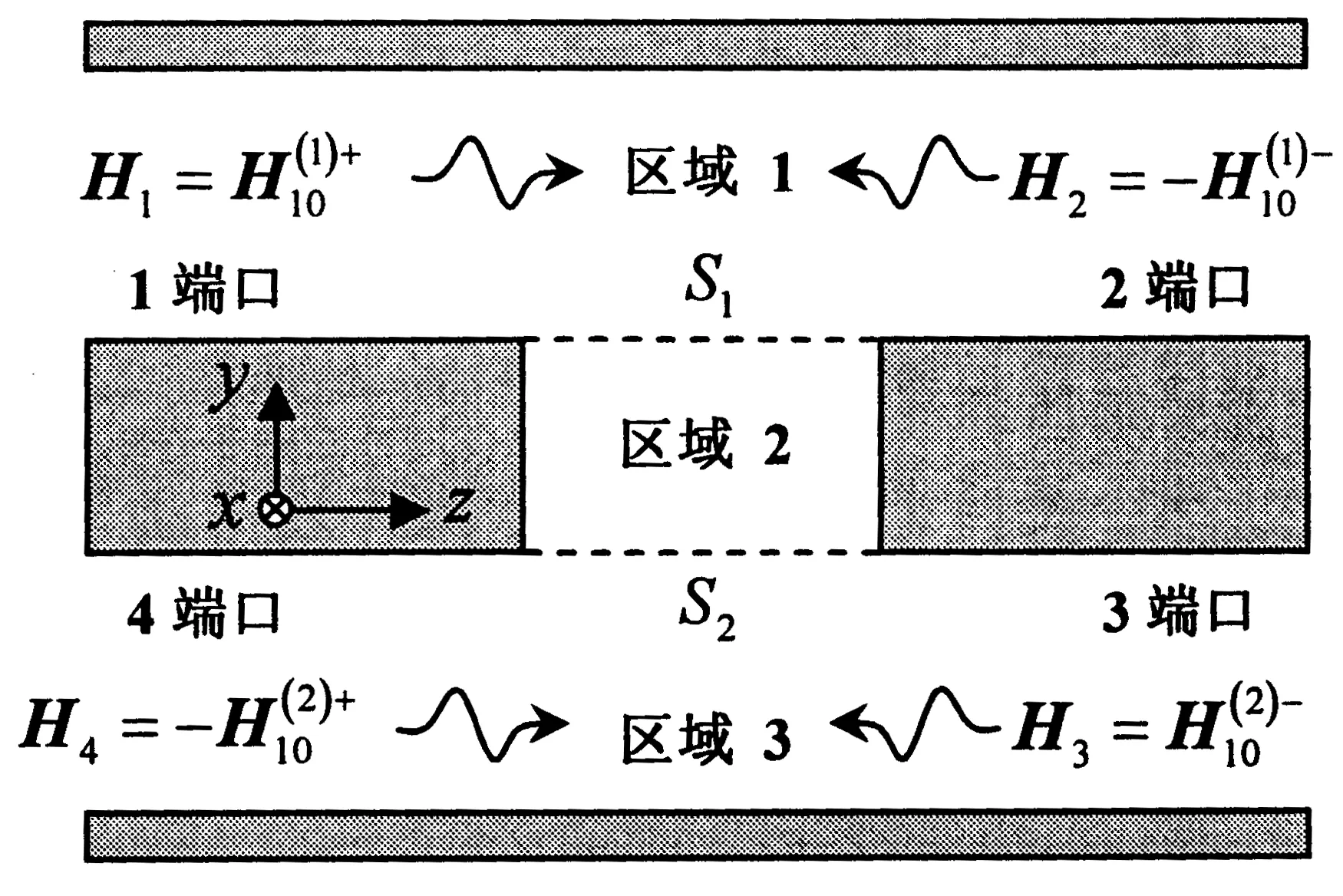
图5 变分法求解Zslot的区域划分与平衡激励分别表示上下层波导TE10模归一化正、反向入射波的磁场分量)

上述过程需要根据两个未知场量ES1与ES2分别选取试函数，增加了求解的计算量。若采用相同的试函数，可以使求解大为简化；然而，在仅有单个入射基模的情况下，ES1与ES2的实际分布存在较大差别，采用相同的试函数将导致较大的误差，如图6(看821页)(a)所示。为此，可采用平衡激励，即令四个依次反相的归一化基模分别从四个端口处同时入射，如图5所示，并根据新的入射场建立变分表达式。从图6(b)可以看出，平衡激励使ES1与ES2的分布趋向一致，因此，可在保证精度的前提下采用相同的即单个试函数以简化求解。根据上述分析，可提取得Zslot的表达式为

其中:

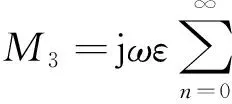
3.2 混合设计方法

H型结混合设计方法的基本步骤如下。首先，根据回波损耗、功分比例等设计指标，以等效电路为基础对H型结进行多次迭代设计，确定各参数的设计初值；此过程仅涉及等效电路的计算，一般可以在短时间内完成。随后，根据各参数的设计初值在全波分析软件中进行建模、仿真和微调优化，确定各参数的优化值。图7为两个H型结的设计例子，设计目标为优化以14.25 GHz为中心的带内回波损耗。从图中可见，当耦合缝隙宽度d增大时，等效电路法的精度有所下降，但仍在可接受范围内。 表1为设计参数的初值与优化值之间的比较，其中|Δ|为设计初值与优化值之差的绝对值；结果表明：由等效电路法所确定的设计初值与由全波分析法所确定的优化值非常接近，可显著减少全波分析的计算量，实现快速、可靠的设计。

表1 例子中设计初值与优化值的比较(单位：mm)

(a) d = 1.2 mm

(b) d = 2.6 mm图7 H型结的设计例子(全波分析使用HFSS)

4. 波导功分网络

H型结具有准一维的结构特征，可实现紧凑的波导功分网络。图8为一种基于H型结的一分四功分网络。如图所示，H型结可显著压缩网络结构在垂直方向上所占用的空间并将其限制在准一维方向(水平方向)内，且分路数越多效果将越明显。因此，H型结在用于波导功分网络设计时比传统T型结更为紧凑，具有一定的优势。

在具体设计中，b1与b3往往不相等，因此功分网络中前级H型结的下层波导与后级H型结的上层波导需要通过矩形波导窄边变换器进行过渡连接。此外，窄边变换器还为两级H型结间相距的电长度提供了一个额外的调节自由度：通过平移变换器，可在不改变物理距离的前提下调整连接路径中两层波导所占的比例；由于窄边变换器存在一定的反射，两层波导按照不同的比例进行组合即可实现不同的电长度连接。这一特性可用于功分网络中内部反射波的相互抵消，从而优化网络的回波损耗；对于输出端口位置已被固定的功分网络，这样的调节方法尤为重要，可极大地方便网络的设计。

图8 基于H型结的一分四波导功分网络

5. 实验验证

5.1 H型结波导功分器

对参数如表1所示的两种H型结波导功分器进行了加工验证。为便于连接测试，在H型结上层波导处增加了90度E面拐角，如图9所示。测试时使用同轴波导转换器作为连接器，测试数据由 Agilent 8722ES 矢量网络分析仪获得。图10的实验结果表明，两种H型结的-15 dB带宽约为2 GHz，相对带宽约为14%，带内插损的典型值为0.5 dB.因实验条件所限，测试参考面仅校准至同轴端口，测试结果与全波分析难免会存在一定的误差。尽管如此，H型结的驻波特性在所需频带内表现优良，与全波分析结果大致吻合，基本验证了H型结的性能及设计方法的有效性。

图9 H型结实物图

5.2 一分四波导功分网络

以表1中d= 1.2 mm的H型结为基础，设计并加工了一分四波导功分网络，结构如图11所示，实验条件与5.1节中相同。图12的实验结果表明，网络的-15 dB带宽约为1.8 GHz，相对带宽约为12.6%，带内插损的典型值为0.7 dB.网络的驻波特性在所需频带内表现优良，与全波分析结果大致吻合。

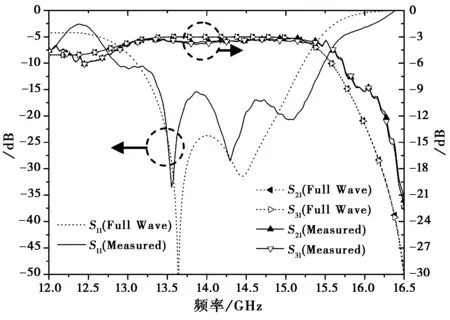
(a) d=1.2 mm

(b) d=2.6 mm图10 H型结的实验结果

图11 基于H型结的一分四波导功分网络

图12 一分四波导功分网络的实验结果

6. 结 论

本文提出了一种新型的H型结波导功分器，具有准一维的结构特征，特别适合于设计紧凑的波导功分网络。通过对H型结的等效电路进行分析，有针对性地在H型结中引入E面阶梯，使其阻抗匹配带宽提高超过两倍，并为进一步改进指出了可能的方向。应用平衡激励，使用变分法对有限壁厚耦合缝隙进行了参数提取，得到了H型结等效电路中Zslot的表达式，从而实现了等效电路的定量分析；结合等效电路法与全波分析法，可对H型结进行快速综合与设计。计算结果显示混合设计方法具有可行性，可在耗时与精度上取得折中。实验结果表明：H型结及基于它设计的波导功分网络具有优良的性能，可作为实用的参考方案。

7. 附 录

如图5所示，根据等效原理、格林函数法及相应的边界条件可获得如下方程组[9-10]

∬S1JM1(r)·H1dS1+∬S1JM1(r)·H2dS1

=-jωε∬S1∬S1JM1(r)·Gm1(r|r′)·

jωε∬S1∬S2JM1(r)·Gm3(r|r′)·

(1)

∬S2-JM2(r)·H3dS2+∬S2-JM2(r)·H4dS2

=-jωε∬S2∬S2JM2(r) ·Gm2(r|r′)·

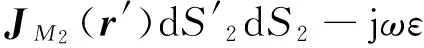
jωε∬S2∬S1JM2(r)·Gm3(r|r′)·

(2)

式中：Gmi(r|r′)为区域i的磁型并矢格林函数，i=1,2,3；并选取试函数

其中h为幅度因子。经运算可知

∬S1JM1(r)·H1dS1=∬S1JM1(r)·H2dS1=hN

∬S2-JM2(r)·H3dS2=∬S2-JM2(r)·H4dS2

=M1

=M2

=M3

=M3

=M4

=M4

因此，式(1)与式(2)可改写为

2hN=-h2(M1+M3-M4)

(3)

(4)

由于该结构具有对称性，其散射参数有如下关系：

S11=S22，S33=S44，S12=1-S11，S34=1-S33，S24=S13，S32=-S31.因此，由简正模法可得

∬S1JM1(r)·H1dS1=∬S1JM1(r)·H2dS1

=-4(S11+S13)

(5)

∬S2-JM2(r)·H3dS2

=∬S2-JM2(r)·H4dS2

=-4(S33+S13)

(6)

〗将式(3)与式(4)两边相加，并联立式(5)、(6)可得

=-h2(M1+M2+2M3-2M4)

于是可构造出(S11+S33+2S13)的变分表达式[10]为

(7)

根据等效电路可知

S11/S33=Z2/Z1=b2/b1

(8)

此外，根据简正模法可知

(9)

最后，将式(8)、(9)代入式(7)，并消去h，最后整理可得

(10)

上式即为图5中1端口反射系数的表达式；再根据等效电路模型获得Zslot与S11的关系，即可提取出Zslot的闭合表达式。

[1] SEHM T, Lehto A, Raisanen A V. A high-gain 58-GHz box-horn array antenna with suppressed grating lobes [J]. IEEE AP, 1999, 47(7):1125-1130.

[2] WU Weiwei,YIN Jiaxian, YUAN Naichang. Design of an efficient x-band waveguide-fed microstrip patch array [J]. IEEE AP, 2007, 55(7):1933-1939.

[3] ARAMAKI Y, et al.. COP millimeter-wave horn array antenna [C]// in Proc. 2008 Intl. Symp. Antennas Propagat. (ISAP2008), pp. 37-40, Oct. 2008.

[4] SONG Kaijun,FAN Yong,ZHANG Yonghong.Eight-Way Substrate Integrated Waveguide Power Divider With Low Insertion Loss [J]. IEEE MTT,2008,56(6):1 473-1477.

[5] 徐俊峰, 洪 伟, 蒯振起，等. 平衡馈电基片集成波导缝隙阵列全向天线 [J]. 电波科学学报, 2008, 23(2):207-210.

XU Junfeng, HONG Wei, KUAI Zhenqi, et al.. Substrate integrated waveguide (SIW) slot array omni-irectional antenna with balanced feeding [J]. Chinese Journal of Radio Science, 2008, 23(2):207-210. (in Chinese)

[6] BIALKOWSKI M E, WARIS V P. Analysis of an N-way radial cavity divider with a coaxial central port and waveguide output ports [J]. IEEE MTT, 1996, 44(11):2010-2016.

[7] 陈明勇,窦文斌. Ka波段径向波导功率合成网络[J]. 电波科学学报, 2010, 25(4):745-748.

CHEN Mingyong, DOU Wenbin, Power combiner using radial waveguide at Ka-band [J]. Chinese Journal of Radio Science, 2010, 25(4):745-748. (in Chinese)

[8] 吴微微,尹家贤,袁乃昌. X波段微带天线阵的新型高效馈电方式研究[J]. 电波科学学报, 2007, 22(5):785-789.

WU Weiwei, YIN Jiaxian, YUAN Naichang. Study of a novel and high efficient feed method for X-and microstrip patch arrays [J]. Chinese Journal of Radio Science, 2007, 22(5):785-789. (in Chinese)

[9] VU KHAC T, CARSON C T. Coupling by slots in rectangular waveguides with arbitrary wall thickness [J]. Electronics Letters, 1972, 8(18):456-458.

[10] SANGSTER A J. Variational method for the analysis of waveguide coupling [C]// Proceedings of the Institution of Electrical Engineers, 1965, 112(12):2171-2179.

[11] LEVY R. Analysis and synthesis of waveguide multi-aperture directional couplers [J]. IEEE MTT, 1968, 16(12):995-1006.

[12] Nathan Marcuvitz. Waveguide handbook [M]. London: The Institution of Engineering and Technology, 1986, Chapter 3, 4, 5.