分段多项式建模校正电离层相位污染算法研究

姜 维 邓维波

(哈尔滨工业大学电子工程技术研究所，黑龙江 哈尔滨 150001)

1． 引 言

超视距雷达是一种利用高频电磁波在电离层与地面之间反射或沿地球表面绕射机制克服地球曲率限制从而探测到地平线以下目标的新体制雷达。超视距雷达主要用于预警，对超低空飞行的飞机、导弹的探测距离远，预警时间长，是低空防御的一种有效探测手段[1]。但由于其工作在高频波段，当电磁波需要通过天波信道进行传输，即电磁波利用电离层反射来实现传播时，复杂和时变的电离层媒介会对电磁波的传输产生诸多影响，进而限制超视距雷达的应用。

由电离层多层结构导致的多模效应和电离层非平稳性引起的相位路径扰动，将使得目标和地、海杂波等的频谱展宽，而杂波的频谱展宽非常容易淹没微弱的目标信号，从而影响雷达的目标探测性能。特别是对于海上慢速目标来说，由于存在强大的海杂波，而舰船的速度与海浪是一个量级，这就导致目标的多普勒频率极为靠近一阶Bragg峰，而在长时间的相干积累过程中，电离层的运动会导致相位路径的改变，这可以看作是对雷达信号进行了相位调制，在多普勒频域表现为信号多了一个多普勒频移。实际上，电离层可能产生的较大扰动会导致雷达回波信号受到正负多普勒频移的影响，进而导致多普勒频谱的展宽，使目标最终仍然淹没在杂波中，这就是电离层相位污染的影响[2]。利用电离层监视探测系统，实时地选择合适的工作频率，可以最大可能地避免多径效应和多模式传播效应[3]。

校正电离层相位污染最直接的方法是在所需探测区内设置应答器，应答转发与其接收到的波形相同的信号，最后将接收站收到的应答信号波形与设定的波形相比较，即可获得电离层相位污染校正函数[4]。然而，在许多实际场合中，并不具备设置应答器的环境条件，而且也无法做到全部探测范围内使用。于是，利用雷达回波中先验已知的杂波信息代替应答器就成为现在研究的主要方向，可以利用的杂波通常有两类：一类是很强的地杂波；另一类是海杂波，它在相邻距离、方位单元为独立分布的随机过程，可以通过统计平均估计出其功率谱。根据具体雷达系统回波谱的实际情况，也可能有其他选择。电离层相位污染导致杂波谱宽展，如果我们能从展宽的杂波中提取相位污染函数，便可以构造出所需的校正函数。利用获得的校正函数对雷达回波信号进行校正，同样可以使回波谱锐化，提高雷达的目标探测性能。目前已有很多方法被提出用来从展宽的杂波中提取电离层相位污染信息，如最大熵估计法[5]、伪维纳(PWVD)分布法[6]、基于特征分解的解污染方法[7]以及合成孔径雷达(SAR)中用于解决相位污染的相位梯度法和最小熵搜索法[8]等。这些方法各有不足，如最大熵估计法假定短时间内电离层是平稳的，而实际上由于电离层的时变性，在短时间内剧烈变化的情形时有发生；伪维纳分布法对信噪比要求很严格，当不满足时会产生较大的估计误差，而在实际中基本都是满足不了的；相位梯度法要求相邻距离和方位的单元具有相同的相位误差，而实际情况是往往难以保证这点，尤其是当电离层变化显著时；基于特征分解的解污染方法计算量大，高精度、实时性的要求不容易满足；最小熵搜索法在电离层非平稳变化剧烈时，耗时很长，也不适合应用于工程实际。近年来，一种基于多项式相位建模的方法得到了大量的研究[9-11]。这种方法把电离层相位污染函数近似为幅度缓变的多项式相位信号，并且利用分段的方法解决电离层变化剧烈的问题，更能真实地反应并得到与电离层相位污染函数相近的校正函数。但是具体应用的时候，还需要考虑一些细节问题，比如阶数如何选择、如何分段等等。前人给出了一些笼统的原则和方法[3,10-13]，但在处理实际数据的时候，由于电离层相位污染的复杂多变性，这些原则和方法，或者太过复杂不适合用在工程实际中，或者不易实现甚至完全失效，影响电离层相位污染的补偿效果，限制了这种校正方法的使用。

文章介绍基于分段多项式建模的电离层相位污染校正算法的基本原理；然后结合实际数据相位污染的特点，讨论如何进行分段更合适，提出相应的阶数选择方法；最后通过实际数据对算法进行验证，同时与采用相位梯度法得到的结果进行比较。

2． 分段多项式建模算法

根据维尔斯特拉斯(Weierstrass)逼近定理，任意有限区间内的连续函数可由一个多项式函数无限逼近[14]。多项式建模解电离层相位污染方法就是将天地波超视距雷达回波信号的瞬时频率或者相位利用一个有限阶的多项式模型来逼近，然后估计出该多项式的各阶系数，重构出瞬时频率或者相位作为估计值。

恒定幅度的M阶多项式相位信号(PPS)定义如下[10]

(1)

式中：N是采样点数，也是数据长度； Δ是采样间隔；b0是常数； 系数am是实数。

PPS的M阶瞬时矩HIMM定义为

(2)

M阶模糊函数HAFM定义为HIMM的离散傅里叶变换，其表达式为

HAFM[s(n),ω,τ] =DTFT{HIMM[s(n),τ]}

exp{-jωnΔ}

(3)

基于HAF的多项式建模相位污染校正算法可以描述如下：

1) 初始化要处理的信号，令m=M以及第m次迭代序列z(m)(n)=y(n)，其中y(n)即为从传感器阵列接收到的数据序列；

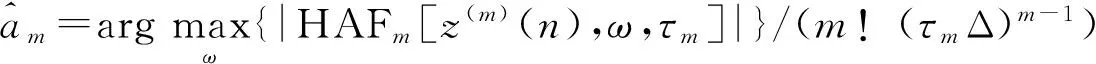
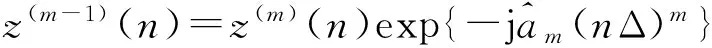
4) 令m=m-1，重复步骤2)直至m<1；

5) 利用极大似然方法估计参数a0和b0，

在加性高斯白噪声环境中，满足一定信噪比(SNR)的条件下，该算法能取得与最优的最大似然估计几乎相同的估计性能，且信号各参数的估计方差接近Cramer-Rao边界，同时，该方法对幅度缓变、非严格PPS仍具有良好的估计性能。在天地波超视距雷达中，由于电离层的时变性，导致电波受到非线性相位调制，此时这种信号就不是严格的PPS。

假设传感器阵列接收的连续采样信号y(n)为

y(n)=b(nΔ)exp[jφ(nΔ)]

0≤n≤N-1

(4)

式中：b(nΔ)是nΔ时刻的幅度，是缓变的；φ(nΔ)是时变相位。根据Weierstrass逼近定理，φ(nΔ)可用一个多项式来近似，但是当φ(nΔ)变化过快时，这个多项式的阶数就会很高(如6阶以上)，此时，所需SNR很高，而在实际情况中是不能满足的，这将直接导致相位污染校正算法失效。文献[11]将信号分成若干段，每一小段数据中φ(nΔ)变化不是很快，可用较低阶的多项式来近似[2]。只要利用基于HAF的多项式建模相位污染校正算法估计出每一小段的多项式的系数和瞬时相位，综合每段的结果便可以得到整个时段信号的瞬时相位，进而对电离层相位污染进行校正，文献中的仿真结果表明其校正性能较好。但是采用分段多项式建模的相位污染校正算法存在两个问题，一个是如何对数据进行分段，另一个是阶数如何选择，它们直接关系着对电离层相位污染函数的描述准确与否，以及校正性能的好坏。

3． 分段原则

关于如何分段，相关文献只是笼统的提出：原则上相位变化快的信号，采用短序列、多段数和高重用率的方案；相位缓变的信号，采用长序列、少段数和低重用率的方案[3,11-13]。具体如何找到合适的分段方式，并没有言明。在实际处理中，对于相位变化快的信号，采用前面的短序列原则，每段32或者16个采样点数，保证高重用率(同时保证了多段数)，每次移动窗移动1或者2个采样点数，相关文献[3][11]-[13]中的相应仿真结果都表明了方法的有效性。但对于相位缓变的情况，讨论较少。而在天地波超视距雷达的实际回波信号中，电离层污染导致的相位缓变情况出现较多，所以，实际需求要求讨论这种情况下的分段原则。

之所以难以给出一个具体的合适分段方式，主要是缺乏衡量一个分段方式好坏的标准。利用算法估计的相位与真实的污染相位之间差值的均方称为相位污染估计的均方误差(MSE)。不同的分段方式对应不同的均方误差，衡量一个分段方式的好坏，不能光看均方误差的数值大小，而是要和相应的均方误差对相位污染补偿后的整体结果的影响结合起来考虑。为了观察不同的均方误差对相位污染补偿后的整体结果的影响，把受到电离层相位污染的某真实信号中零频处的单频信号抽取出来，将不同数量级均方误差(对应不同分段方式、涉及每段的阶数选择采用相同的固定阶数)对应的补偿后的不同结果画在同一个图上进行比较，如图1所示。这里给出的结果为了仅分析相位污染造成的影响，已经排除了其它的影响因素，如“跳变”现象、幅度污染等。图1中实线对应的是不存在相位污染的理想单频信号的结果，点线均方误差2.9251e-8对应的结果较好地补偿了相位污染，其他结果虽然在频谱中心部分也较好地实现了相位污染补偿，但是随着均方误差数量级的增加，旁瓣和整个频谱的噪底也不断抬高，这势必会对整个信号频谱零频以外的其他频谱信息造成影响，如破坏频谱结构、淹没目标信息等。当然我们希望均方误差越小越好，但并不是说尽可能小，实际上数据长度、信噪比等也决定了不可能无限小。利用图1，结合实际数据的处理结果，分析表明当均方误差小于1e-5时，旁瓣和整个频谱噪底的抬高对整个信号频谱零频以外的其他频谱信息的影响可以忽略；当均方误差大于1e-5时，其影响不可忽略，这样的结果也是我们所不希望的。给出的结论是针对我们实际信号中信噪比为10～30 dB的一般情况，当出现信噪比很大或者由于干扰严重导致信噪比很小的个别情况，相应的门限也应该增大或者减小。

利用上述结论来分析相位缓变的信号应该选择的分段长度。给出信号s1(n)、s2(n)和s3(n)分别代表标准的多项式相位信号、非严格的多项式相位信号以及真实的信号。其中s1(n)=exp{j(1+0.001n)}，s2(n)=exp(-jπsin(2π0.0002n)},s3(n)为任意截取的一段真实信号，所以无法给出解析表达式，数据长度为512。三种信号对应的相位如图2所示，可以看出都是相位缓变的信号，而且是变化非常缓慢。另外s1(n)和s2(n)都添加高斯噪声使其信噪比为16 dB.分别给出其在相同重用率条件下不同分段长度下的估计均方误差结果(每段数据的阶数选择都采用相同的固定阶数)，如表1所示。由表1可以看出，分段长度不能太长，即使对于相位缓变的信号来说，考虑均方误差因素，也应该选择短序列。对大量其他的真实数据进行类似分析，也可以得到相同的结论。分段长度也不是长度越短越好，它还受信噪比和阶数的限制，关于这点文献[10]中有较详细的推导和讨论，这里不再赘述。综合前面的各种因素考虑，分段长度以选择20～40为宜。同样的，当出现信噪比很大或者很小的个别情况，相应的分段长度也可以更小或者必须增加。

表1 s1、s2、s3三种信号在不同分段长度下的均方误差结果

关于分段数和重用率，这实际上是一个问题，在分段长度一定的情况下，重用率越高，分段数就越多，反之，重用率越低，分段数就越少。针对实际信号，在分段长度分别设定为32(短序列)和128(长序列)的情况下，给出不同重用率下的均方误差结果(每段数据的阶数选择同样都采用相同的固定阶数)，如表2和表3所示。由表中的结果可以看到，即使在长序列的情况下，均方误差也是随着重用率的增高而不断降低的。重用率越高，用于某时刻的瞬时相位估计值的修正值就越多，估计的均方误差也就越小，实际结果与理论分析的结论相吻合。因此，无论是短序列，还是长序列的情况下，都应该采用高重用率的原则。具体算法可采用任意截取数据中一段，在分段长度已经确定的情况下，计算不同重用率下的均方误差，根据对均方误差的要求，选择相对应的重用率来处理这批数据。

综合前面的分析可知，对相位缓变信号在分段问题上，也应该采用短序列、多段数和高重用率的方案。与之前采用长序列、少段数和低重用率的方案相比，新方案可以明显减小均方误差。实际工程中，一般情况下分段长度选择20～40，移动点数选择2～4。

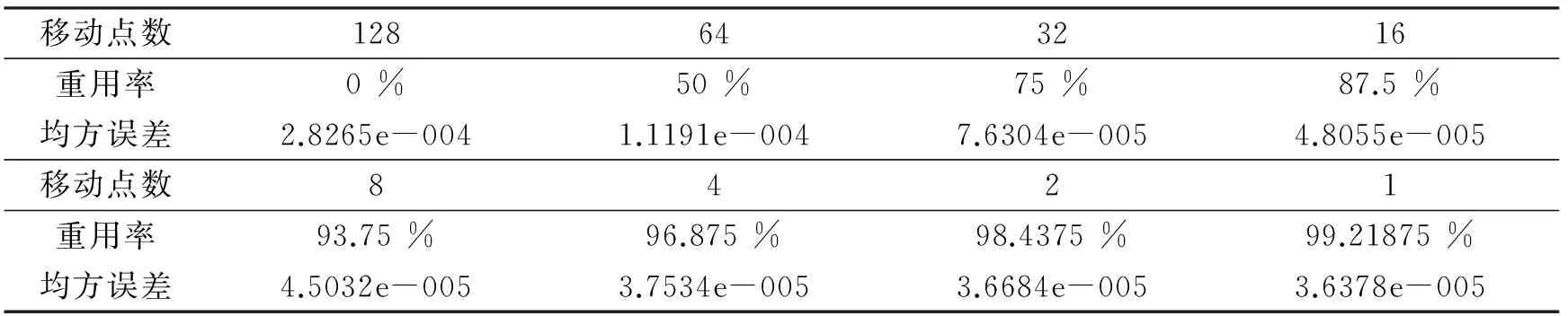
表2 分段长度为128时不同重用率下的均方误差

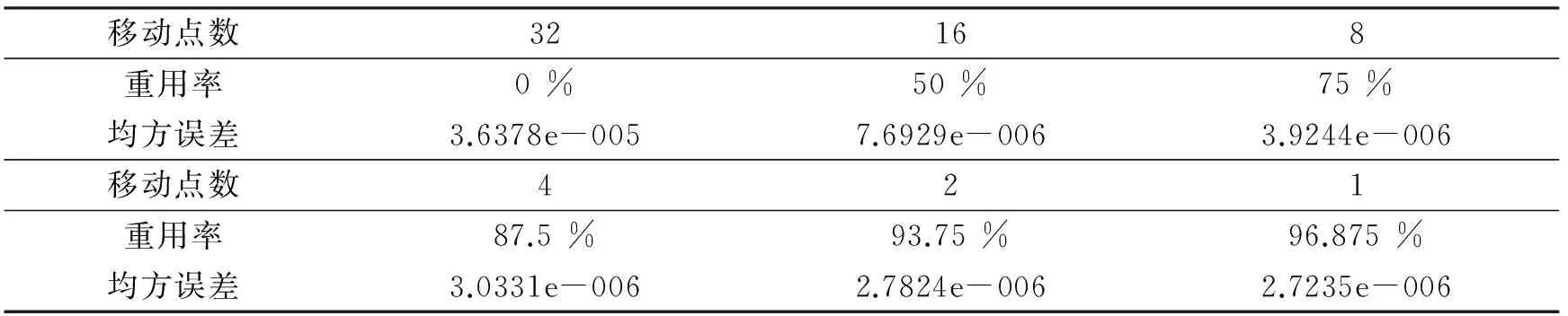
表3 分段长度为32时不同重用率下的均方误差

图2 三种信号的相位

4． 阶数选择

如何合理的分段并为每段数据选择合适的模型阶数是分段多项式相位建模算法的核心。解决如何分段的问题之后，下一步需要解决的问题就是如何为每段数据选择模型阶数。如果模型阶数选得过低，由于不能表征信号相位的真实变化情况，导致建模误差增大；如果模型阶数选得过高，虽然可以减小建模误差，但估计的均方误差则会增大，甚至导致整个相位估计算法的失效[3]。因此，必须选择合适的模型阶数。

建筑的外围护结构由当地热惰性较好的厚重石材砌筑，石材两侧分别用15mm厚的砂浆填缝、包裹，建筑最内层涂抹10mm厚的石膏层。在近年新修或改造的建筑中，为更好地隔绝外部炎热的环境，石膏层下方还会添加一层60mm厚的绝缘聚苯乙烯和10mm左右的空气间层作为绝热层。

针对这个问题，文献[3]给出了三个自适应选择多项式建模阶数的准则：基于谱线识别可靠性准则的阶数选择、基于最大似然原理的阶数选择，基于最小熵原理的阶数选择。文献[12]的分析表明后两种方法虽然确定模型阶数准确，但计算量太大，工程中很难应用。同时结合第一种方法，提出频域法和时域法两种工程中比较实用的阶数选择简单方法，并且指出频域法的适用性更广。

频域法判断多项式相位信号s(n)模型阶数的具体步骤如下[12]：

1) 假设HAF变换阶数初始值M1=1；

2) 对s(n)做M1阶的HAF变换；

3) 若HAF变换将多项式相位信号变换为一个非零的单频信号，则执行步骤4)；否则M1=M1+1，重复步骤2)；

对实际信号进行电离层相位污染校正的时候，当相位变化比较缓慢时，由于采用短序列，每段数据的长度非常有限，信噪比也会发生变化，此时采用频域法判断阶数会变得比较困难，而时域法则是完全失效。对于图2中对应的真实信号进行分段，分段长度为32，采用频域法对第一段长度为32点的数据进行阶数判断，其一阶和二阶HAF的结果分别如图3的实线和虚线所示。判定中，对数据进行HIM操作会使得数据的有效点数减少，这会导致HAF谱上得到的分辨率较低，而短序列这个条件更会加剧分辨率的下降。由图3可以看出，此时已经很难判断出阶数，二者基本都位于零频。HAF谱是通过补零FFT来获得的，当补零后长度达到4096点时，二者才能在频谱上分开，而且也只相隔一个点，此时可以判断阶数为1阶；如果补零长度不够长(比如1024点)，则完全判断不出来，频域法失效。另外，对实际信号进行电离层相位污染校正的时候，还发现一个有趣的现象，即只要选择的阶数为2～5中的任意一个，补偿结果都跟选择的阶数为1时一样，相应的估计均方误差也完全一样。详细分析可知，当选择的阶数大于1的时候，此时利用基于HAF的多项式建模相位污染校正算法估计的二阶以及二阶以上的高阶多项式系数都是零，所以结果没有变化。此时估计的均方误差不会随选择的阶数增大而增大，而是个定值；同时建模误差也不会随选择的阶数变化而变化，也是个定值。从这个角度出发，可以简化阶数选择方法，进一步提高计算效率和适用范围。

图3 长度为32点的真实数据的一阶 和二阶HAF变换幅度图

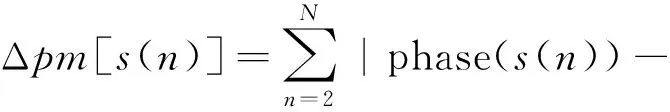
phase(s(n-1))|

(5)

Δpf[s(n)]= Δpm[s(n)]/|max{phase[s(n)]}-

min{phase[s(n)]}|

(6)

式中：N是信号的数据长度； Δpm≥0； Δpf≥1。在此定义之下，具体来说，没有添加噪声的情况下，如果信号的相位变化Δpm小于0.1，那么针对前面两种信号的估计结果都会出现前述的类似现象。在没有添加噪声的情况下，进一步的分析可以得出如下结论：

1) 对于标准的多项式相位信号而言，其估计均方误差都会随着选择的阶数增加而不断减小，直至增加到某一阶数之后估计均方误差就不再变化，我们把这个阶数称为稳定阶数。稳定阶数小于或者等于信号的真实阶数，稳定阶数受信号的相位变化大小影响。信号的相位变化Δpm小于1时，即相位变化较小时，稳定阶数小于或者等于信号的真实阶数；信号的相位变化Δpm大于1.5时，即相位变化较大时，稳定阶数等于信号的真实阶数。相位变化越小，稳定阶数也就越小。如大多数情况下，相位变化Δpm小于0.1时，稳定阶数为1，这种情况就对应前面提到的特殊现象。

2) 对于非严格的多项式相位信号，也有类似的结论，同时也有区别。因为只有在相位变化满足一定的条件之下，相位估计算法才存在前面提到的稳定阶数。当信号的相位变化Δpm小于1、Δpf=1时，存在稳定阶数，且稳定阶数为1，这种情况即对应前面提到的特殊现象；当信号的相位变化Δpm小于1、1<Δpf<3时，存在稳定阶数，且稳定阶数为大于1的正整数，稳定阶数受Δpf的影响，Δpf越大，稳定阶数就越大，此时，估计均方误差会随着选择阶数的增加而不断趋于稳定阶数时的均方误差；其他情况下，即相位变化满足Δpm大于1和Δpf>3两个条件之中的任意一个时，没有明显规律，前面的各种情况都有可能出现，甚至可能出现稳定阶数不存在的情况。

上述结果是在没有添加噪声的情况下得出的，前面的仿真还表明，当信噪比较大的情况下(即噪声对信号的影响基本可以忽略不计)，也可以得到同样的结果。在电离层相位污染校正算法中，用来提取相位污染函数的原本就是频谱中比较强(信噪比比较大)的成分，如地杂波、直达波、海杂波等，在解污染前期处理中对其进行滤波提取时，关心的信号(如地杂波等)能量基本被完全滤出，而噪声的能量只有滤波器通带内的很小部分被滤出，这就导致最后滤出的用来提取相位污染函数的信号的信噪比得到极大的提高，所以，实际的真实信号基本都是满足前面的信噪比要求的，个别噪声占优(整个频谱被噪声彻底淹没)的极端情况例外。因此，分段后的信号，绝大部分都是属于噪声对信号的影响非常小可以忽略的情况。对于个别噪声对信号的影响不能忽略的情况，这时就算使用频域法，对于有噪标准的多项式相位信号，当相位变化缓慢时频域法失效，而对于有噪非严格的多项式相位信号，当相位变化剧烈时频域法也失效，因此，此时只能考虑其他方法，如较复杂的基于最大似然原理的阶数选择方法等。

综合前面关于稳定阶数的讨论，结合实际信号的处理需要，同时考虑基于HAF的多项式建模相位污染校正算法本身对阶数的限制，即阶数不能超过5[11]，对改进的阶数选择方法——基于相位变化的阶数选择。其阶数选择的具体步骤是：对于每个分段数据，首先计算表征数据相位变化的Δpm和Δpf，然后根据Δpm和Δpf的大小采用不同的方法；若同时满足Δpm和Δpf<3，那么采用固定阶数，选择阶数为5，否则，采用频域法判断阶数。

与直接采用频域法相比，改进的阶数选择方法在相位变化较小的时候，采用固定阶数，避开了短序列等造成HAF频谱分辨率下降、频域法不易判断或者完全失效的情况；同时计算Δpm和Δpf只需进行一些简单的四则运算，不再需要进行HAF变换、产生HAF幅度谱、判断单频及其位置等，这就大大简化了阶数选择方法的复杂度，提高了计算速率。在相位变化剧烈的时候，还是采用频域法，与之前相比只是增加了Δpm和Δpf的计算量，这是可以接受的。此外，实际信号的分析结果也表明：在数据采用2.2的原则分段后，绝大多数短序列都是满足相位变化较小的条件的。以某天地波雷达系统接收的回波数据为例，利用某个距离的海杂波提取相位污染函数，滤波后的信号分段后，满足Δpm<1和Δpf=1的段数占总分段数的88.2%，满足Δpm<1和1<Δpf<3的段数占11.8%，不存在其他情况，即全部满足条件。同样，利用直达波提取相位污染函数，滤波后的信号分段后也有类似结果，相应的比率分别为91.05%和8.95%。这就说明了改进阶数选择方法的有效性，并且更适合应用于工程实际。当然，由于算法在相位变化较快时仍然采用前人的方法，这些方法的有效性在仿真数据的条件下已经得到了很好的验证，但并没有在实际数据中得到验证；所以，如果对于其他雷达系统的回波数据，出现分段后数据的相位变化过大同时前人的方法处理能力有限的情况，那么本算法的有效性也会受到影响。

5． 实际数据验证

现有电离层相位污染校正算法的研究，验证算法的有效性多利用高频地波雷达数据人为添加相位污染函数来实现。由于用来验证算法的数据中不存在其他电离层污染，同时添加的都是具有解析表达式的相位污染函数，大多数算法都可以获得较好的补偿结果。然而，当处理实际通过电离层传播的真实回波信号时，除了电离层相位污染，由于还存在其他不可避免的电离层相关污染，以及真实的相位污染函数可能无法用解析表达式表示，此时大多数电离层污染校正算法的补偿效果都很有限，甚至失效。

某工作频率为10.285 MHz的回波数据对应的一段真实相位污染如图4中实线所示。分别利用相位梯度法(PGA)和改进分段多项式建模算法(PPPMA)来从回波数据中提取相位污染信息，并与真实的相位污染进行比较。其中，采用改进的算法时，分段原则采用短序列、多段数和高重用率的方案，每段的阶数选择则采用第4节中所述的改进的阶数选择方法。相位梯度法则利用了邻近的10个距离单元的信息来减小误差。两种方法提取的相位污染结果如图4所示，由图4可以看到利用改进算法所获得的结果几乎跟真实相位污染完全重合，而相位梯度法的结果则与真实相位污染有一定差别。分析其原因，主要是由于相位梯度法要求相邻距离和方位的单元具有相同的相位污染，而这里的实际数据显然并不满足这个条件，所以导致相位梯度法的结果存在一定误差。此外，两种方法所对应的均方误差分别为1.3663e-006和0.4449，从这个角度也可以证明改进的方法对于真实数据更有效。如果采用未改进的分段多项式建模算法，正如第4部分前面给出的分析那样，部分分段后的短序列会出现无法判断阶数的情况，即阶数选择方法完全失效，这就会导致整个算法出错停止，无法得出任何结果。

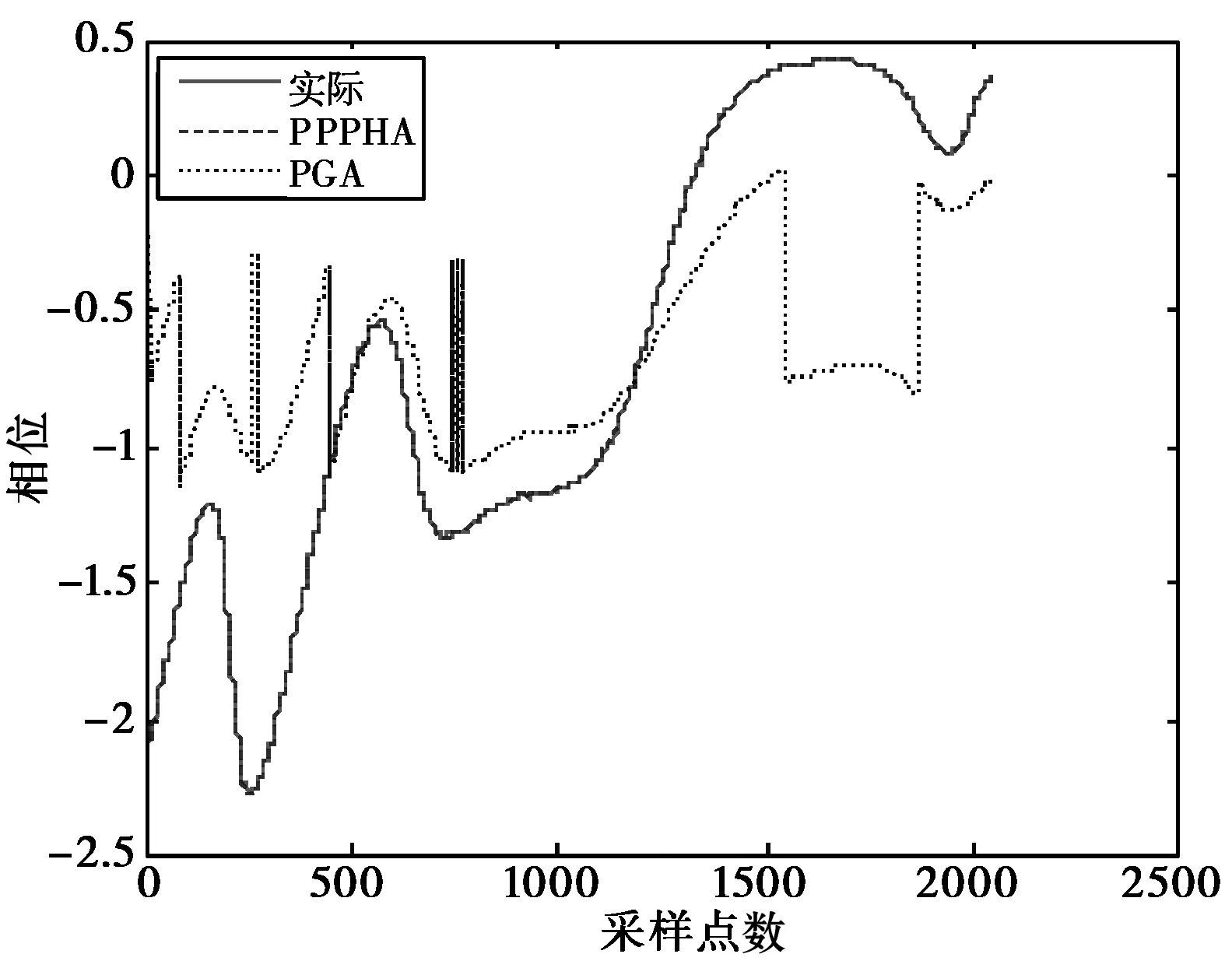
图4 两种不同方法提取相位污染的结果比较

利用某试验天地波雷达系统获得的回波数据来观察本算法的补偿结果，其工作频率为9.083 MHz，调频周期为0.021 s，相干积累时间为40.96 s.其中某个距离单元功率谱的补偿结果如图5所示。其中实线对应的是未补偿前的结果，右侧0.2325 Hz处强大的一阶Bragg峰清晰可见，因此，这里选择海杂波作为提取相位污染信息的参考信号。Bragg峰一般成对出现，这里可能由于海风的影响，左侧的Bragg峰并不明显。另外还可以看到位于约0.1628 Hz处的疑似目标信号，由于电离层污染的存在，图中目标信号和海杂波的频谱都有所展宽，且相互交叠。实际上，若非跟后续补偿之后的结果做比较，在没有先验已知的条件下，尚不能确定0.1628 Hz处的疑似目标信号身份，即目标信号不易分辨。采用前面所述电离层相位污染校正算法对其补偿之后的结果如图5中虚线所示，由图可以看到，目标信号和海杂波的频谱都得到了锐化，明显跟海杂波分离的0.1628 Hz处的疑似目标更加清晰可辨。同时在海杂波右侧0.3023 Hz处，原本由于海杂波展宽而被彻底淹没的另一个疑似目标信号也因海杂波的变窄而显现出来，这些都说明了前面所述电离层相位污染校正算法的有效性。需要说明的是，由图5可以看到，虽然该校正算法有一定的补偿效果，但并没有将海杂波的频谱宽度补偿回到理想信号三根谱线的结果。本试验雷达系统的体制决定了本系统中海杂波的展宽并不仅仅是电离层相位污染的结果，而是由电离层污染和双基地角的存在共同作用的结果。因此，即便通过电离层污染校正算法补偿了电离层的影响，但由于双基地角的存在，海杂波还是会存在一定程度的展宽。另外，图5的结果并不是仅进行电离层相位污染校正就能得到的，而是对其他电离层的影响也进行一定程度地相应处理，这里由于篇幅所限，不再详述。

图5 某个距离单元的功率谱的补偿效果

6． 结 论

在原有的基于分段多项式建模的电离层相位污染校正方法的基础上，结合试验雷达系统所获得实际数据的相位污染特点，针对原有方法部分处理细节上的不适用性，分析给出了相位缓变信号应采用的分段原则，提出了改进的阶数选择方法，减小了原有算法的复杂度，提高了算法效率，特别是对于实际数据中常出现的分段后每段数据相位变化很小的情况，算法的改善效果更加明显。实际数据的处理结果表明了算法的有效性，也表明该算法更适合应用于工程实际。电离层的影响并不仅仅是相位污染的问题，其他电离层污染如幅度污染等也会对目标检测产生影响，因此，对其他电离层污染的分析以及如何校正则是后续还需要研究的问题。

[1] HEADRICK J M, THOMASON J F. Application of high frequency radar[J]. Radio Sci., 1998, 33(4): 1045-1054.

[2] 姬勇力, 江长荫. 返回散射回波去电离层相位污染方法比较与分析[J]. 电波科学学报, 2008, 23(3): 484-490.

JI Yongli, JIANG Changyin. Comparison and anyalysis of ionospheric phase decontamination methods for backscattered signals[J]. Chinese Journal of Radio Science, 2008, 23(3): 484-490. (in Chinese)

[3] 刘颜回, 聂在平, 赵志钦. 改进的分段多项式建模的电离层相位去污染新方法[J]. 电波科学学报, 2008, 23(3): 476-483.

LIU Yanhui, NIE Zaiping, ZHAO Zhiqin. A new method based on improved piecewise polynomial phase model to correct ionospheric phase contamination[J]. Chinese Journal of Radio Science, 2008, 23(3): 476-483. (in Chinese)

[4] 韩蕴洁, 杨志群, 储晓彬. 天波雷达检测舰船时电离层失真的校正方法研究[J]. 现代雷达, 2003, 25(10): 5-8.

HAN Yunjie, YANG Zhiqun, CHU Xiaobin. Research on the correction of ionospheric distortion for ship detection in OTHR[J]. Modern Radar, 2003, 25(10): 5-8. (in Chinese)

[5] BOURDILLON A, GAUTHIER F, PARENT J. Use of maximum entropy spectral analysis to improve ship detection by over-the-horizon radar[J]. Radio Science, 1987, 22(2): 313-320.

[6] HOWLAND P E, COOPER D C. Use of the Wigner-Ville distribution to compensate for ionospheric layer movement in high-frequency sky-wave radar systems[J]. IEEE Proceedings-F, 1993, 140(1): 29-36.

[7] ANDERSON S J, ABRAMOVICH Y I. A unified approach to detection, classification, and correction of ionospheric distortion in HF sky wave radar systems[J]. Radio Science, 1998, 33(4): 1055-1067.

[8] 邢孟道, 保 铮. 电离层电波传播相位污染校正[J]. 电波科学学报, 2002, 17(2): 129-133.

XING Mengdao, BAO Zheng. Phase perturbation correction in ionospheric electromagnetic wave propagation[J]. Chinese Journal of Radio Science, 2002, 17(2): 129-133. (in Chinese)

[9] PELEG S, PORAT B, FRIEDLANDER B. The achievable accuracy in estimating the instantaneous phase and frequency of a constant amplitude signal[J]. IEEE Transactions on Signal Processing, 1993, 41(6): 2116-2224.

[10] PELEG S, FRIEDLANDER B. The discrete polynomial-phase transform[J]. IEEE Transactions on Signal Processing, 1995, 43(8): 1901-1914.

[11] LU Kun, WANG Jiong, LIU Xingzhao. A piecewise parametric method based on polynomial phase model to compensate ionospheric phase contamination[C]//Proc. of ICASSP '03. HongKong, China, 2003: 405-409.

[12] 李 雪, 邓维波, 焦培南, 等. 多项式建模解电离层相位污染阶数选择新方法[J]. 电波科学学报, 2009, 24(6): 1094-1098.

LI Xue, DENG Weibo, JIAO Peinan, et al. Novel order-select method of polynomial modeling for ionosphere phase perturbation correction[J]. Chinese Journal of Radio Science, 2008, 23(3): 476-483. (in Chinese)

[13] 卢 琨, 刘兴钊. 短序列条件下基于分段多项式建模方法的相位估计性能分析[J]. 电子与信息学报, 2005, 27(4): 523-526.

LU Kun, LIU Xingzhao. Phase estimation accuracy based on piecewise polynomial-phase modeling method with short sequences[J]. Journal of Electronics and Information Technology, 2005, 27(4): 523-526. (in Chinese)

[14] 沈燮昌. 多项式最佳逼近的实现[M]. 上海科学技术出版社, 1984.