辅助方程－双向隐式差分法的电磁散射研究

汤 炜 胡茂兵

（华侨大学信息学院，福建 厦门361021）

1.引 言

众所周知，时域有限差分法（FDTD）［1］是电磁学领域一种非常有效的数值计算方法，已广泛应用于电磁散射、天线、电磁兼容、生物电磁场［1］以及电波传播等问题的计算与模拟。但由于FDTD是显式差分方法，其时空步长要满足稳定性条件要求，严格的时间空间步长导致计算效率较低。随后学者们提出伪谱时域差分（PSTD），时域多分辨小波（MRTD）用以改进传统方法。这两种方法对空间步长的选择有一定的改善效率但低下的问题并没有得到完全解决。

日本学者 Namiki［2－3］将交替隐式差分格式应用到FDTD技术中，提出了ADI－FDTD算法，这一方法的提出迄今仍吸引了国际及国内学者的广泛关注［4－6］。国内 方 面，高 本 庆［7］，汤 炜［8－9］，吕 善 伟［10］，葛德彪［11］等人都对该方法进行了一定的研究。但是遗憾的是，由于方程的复杂性使得采用ADIFDTD方法进行三维目标计算论文相对较少。文献［12］提出在整个计算区域都采用分裂场使ADIFDTD方法得到一定的简化，并用该方法计算了三维目标的散射问题。而本文则是在原有的基础上，进一步完成色散媒质的电磁仿真。

关于色散媒质的研究无论在军用还是民用都具有重要意义，如电磁屏蔽，信道衰减等。FDTD技术中色散媒质的电磁模拟大体有以下几种方法，依次为分段线性递推卷积方法 （PLRC）［13］，Z 变 换 方法［14］，辅助差分方程方法（ADEs）［15］，电流密度卷积［16］。几种方法中 ADEs直接从最基本的 Maxwell方程得出，相对简单而且物理意义明确直观。本文以该方法为基础，推导了ADEs－ADI－FDTD方法的迭代方程，并利用算例对这一方法进行了数值验证及时间上的对比。

2.ADEs方法简述［15］

为了后面阐述的方便，在此对ADEs方法进行简单描述。一阶Debye媒质的极化强度P与电场E的关系可以描述为

式中：εs和ε∞分别为0频及∞频时媒质相对介电常数；τ为媒质分子的驰豫时间。将上式写为时域形式，有

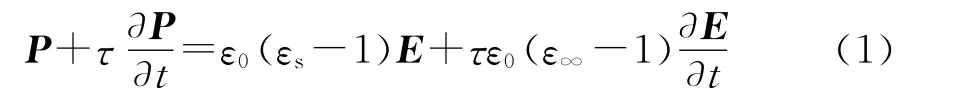
利用D（ω）＝ε0E（ω）＋P（ω），并将其带入磁场旋度方程，可得

同时根据电场旋度方程，即

方程（1）～（3）即构成了ADEs方法的核心方程，相比传统的FDTD方法，增加极化强度P的迭代方程，故称之为辅助方程方法。

辅助方程中极化强度P的时间和空间抽样与电场相同，两者具有空间位置与时刻相同的特点，故利用方程（1）即可完成对P的时间步进。

3.ADE－ADI－FDTD迭代方程的推导

3.1 全分裂场的ADI－FDTD简述

一维和二维ADI－FDTD方法由于场量较少故相对简单，而三维问题相对复杂，同时散射问题中存在吸收边界与连接边界。图1简单显示该方法中迭代所涉及场量及其空间分布，其中包含四个元胞中的11个场量。当元胞跨越吸收边界、连接边界时，需对各场量的跨越作出大量的判断，实现上出现极大困难。

图1 传统ADI－FDTD方法Ex迭代涉及场量及空间分布

本文采用分裂场方法［12］以避免出现上述情况，也即全部区域都如PML层中，将常规场量进行分裂。以Ex及Px为例，其分裂场及方程分别为

进而对微分方程进行ADI技术处理。PML层中虚拟的是各向异性媒质，而各向同性媒质可作特殊各向异性媒质处理，故在空间预先设定好各元胞电磁参数，即可消除PML吸收层与散射场区边界处的跨越问题。

相比传统FDTD方法，本文边界条件是利用两个分裂场量实现的。假设计算区域的总场区域限定在范围内，FDTD方法中根据迭代方程所涉及场量分布，在跨越以下散射场－总场边界时需要考虑连接边界条件：

而分裂场中，方程（5）涉及场量为沿着y轴分布的三个场量，仅在边界1），2）时需要考虑边界条件；与之对应方程（6）涉及场量为沿着z轴分布的三个场量，仅在边界3），4）时需要考虑边界条件。综合两者可以看出分裂场方法与传统方法在边界条件上是一致的。

3.2 ADEs－ADI－FDTD方法

3.2.1 极化强度场的迭代

在 ADEs－ADI－FDTD 中，极 化 强 度 也 进 行分裂，可得

方程（1）中场量均只出现对时间的导数，可假设极化强度与电场在时间空间的抽样完全相同，进一步可得电场与极化强度P的步进表达式。ADI－FDTD方法中场量时间步进是以0.5时间步迭代进行的，以n→n＋0.5为例可得

极化强度n＋0.5→n＋1的迭代也有相同的系数和类似的表达式。

3.2.2 电场与磁场在第一时间分步的迭代

限于篇幅，本文仅仅以相关分量在第一时间分步迭代为例来推导该方法的步进方程，其他场量均可类推。提取方程（2）中x分量并将其改写为分裂场形式。

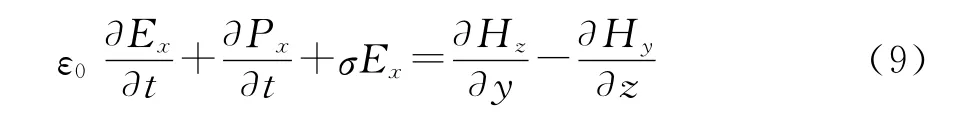
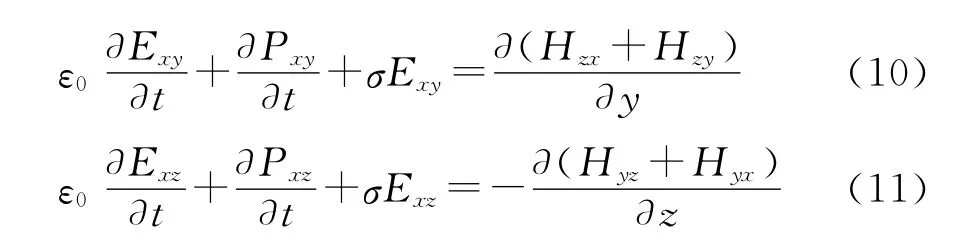
按照第一时间分步的差分特点，方程（9）和（10）可分别写成如下步进方程

为便于突出重点，以（＊）缩写形式表示与方程左边场量空间下标相同，下同。式中S，T为关于媒质、时空步长有关的参数。

考察方程（12），可以注意到方程的右边均为时刻场量，该方程的表达形式与传统FDTD方法类似，可以直接进行场量更新。在ADEs－ADI－FDTD方法中，能够直接更新的场量有第一时间分步中的Exy，Eyz，Ezx，Hxz，Hyx，Hzy及第二时间分步中的Exz，Eyx，Ezy，Hxy，Hyz，Hzx，这些场量均可以在各自时间分步中提前完成并处理好连接边界条件。

而方程（13）右边磁场分量均为（n＋0.5）时刻，不能直接进行迭代。但是幸运的是分裂场Hyx可以预先完成更新，因此它虽与方程左边为相同时刻场量，但为已知量不需考虑处理。故仅剩下Hyz需要处理，按照ADI－FDTD方法，可写出这一时间分步中Ηyz迭代方程：

与前面类似，以（＃）表示与方程左边场量的空间位置在x，y方向相同，下同。方程（13）右边Exy为直接迭代场量，故未知量仅为Exz.根据式（14）可以写出的方程，并与式（13）代入（15）整理可得：

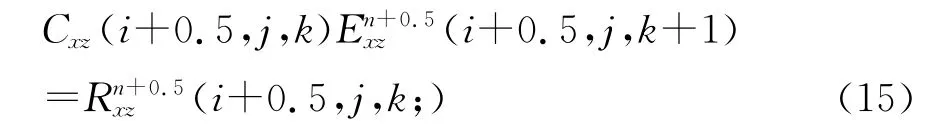
式中：

虽然方程（15）的左边为三个后时刻的电场量，但该方程可以通过追赶法进行求解，从而完成一列电场的步进。

第一与第二时间分步中间接迭代场量都可以按照类似的方法完成场量的步进，进而完成所有场量的更新。

3.2.3 关于时间步长的选择

本文方法中计算空间采用分裂场形式进行电磁仿真，在一定程度上增加了内存的占用，但是另一方面由于时间步长的无约束性（在实际计算过程中时间步长不能设置太大。ADI技术仅保证迭代过程中不产生数值发散现象，并不能保证计算正确。对于时间的抽样仍需要满足对入射波信号的抽样定律，最小抽样频率为所关心最高频率的2倍，另抽样间隔较大，会导致计算结果出现Gibbs现象，降低计算精度），时间步长可以达到传统FDTD技术的10倍以下，时间步长的增加也即意味着仿真过程中时间步数减少，提高了FDTD的计算效率。

4.色散媒质的电磁仿真

为了验证上述公式推导的正确性，体现本文方法的优势，本文通过三维算例对电磁波与色散媒质的作用过程进行模拟。在以下的计算中时空步长的选择依据如下原则

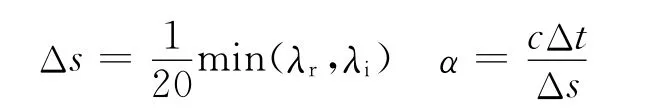
式中：λr，λi分别为最高频率对应实波长与虚波长；α为时空约束常数，FDTD计算时为0.5，对该参数的设定可得不同的时间步长进行计算。

4.1 水泡的后向散射截面

水作为一种常见媒质，测试结果显示零频介电常数εs＝81，无穷频率介电常数ε∞＝1.8，驰豫时间τ＝9.4×10－12，本文所示的双层球为一个水泡。水泡外径和内径分别为0.158mm和0.105mm.受到实波数和虚波数的限制，空间步长Δs＝4μm，其后向散射系数的频响特性如图2所示。

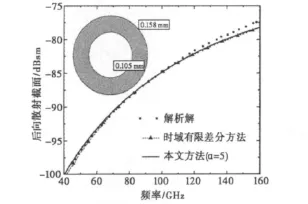
图2 水泡后向散射的频响特性

对该模型先后采用解析方法，ADEs－FDTD和ADEs－ADI－FDTD等三种方法进行了模拟。其中ADEs－ADI－FDTD时间步长根据取值，所得结果与理论结果吻合很好，验证了色散媒质ADI－FDTD方法的计算精度和有效性。从算例尺寸来看，由于在最高频率目标的电尺寸仍然处于瑞利区，其单站雷达散射截面呈单调上升区间。针对上面算例，本文对FDTD与ADI－FDTD的时间步长、时间步数以及程序运行时间进行比较，其结果如表1所示。

表1 传统方法与本文方法计算时间比较

4.2 Von Karman型金属体覆盖非磁性等离子体时的后向散射［17］

各向同性等离子体属于常见的色散媒质，通过参数之间的变换可以将其转变为具有导电损耗Debye媒质的表达形式。本文在此计算Von Karman型金属体覆盖等离子体时的截面。计算模型如图3所示。其中D1＝0.1m，D2＝0.2m，L1＝0.2m，L2＝0.4m.电磁波迎头入射，FDTD计算时取离散间隔δ＝3.33mm.等离子体的浓度N0＝5.0×1017m－3，电子碰撞频率ωeff＝2.0×1010Hz.图4是后向雷达散射截面，分别给出了未覆盖等离子体时和有等离子体覆盖时的计算结果。由图可见等离子体覆盖层在3～7GHz频段里减小了后向RCS.

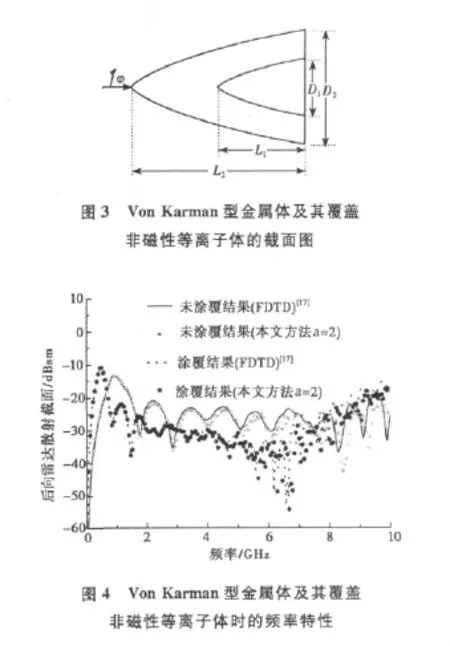
需要说明的是，算例由于受到频谱较宽和计算机内存的限制，空间步长没有取得足够细，因此当约束参数为4和5时，计算结果精度不是很好，论文在此设置该参数为2，计算结果与FDTD计算结果吻合较好。可以说明该方法在计算较为复杂的目标时，仍然是可行及可靠的。

5.结 论

用ADEs－ADI－FDTD方程对色散媒质与电磁波的作用进行了仿真，计算结果表明，该方法能够有效模拟这一过程，计算精度比较高。时间步长的增加减少了迭代次数，使计算效率有极大提高。三维算例表明ADEs－ADI－FDTD方法的耗时仅仅为传统FDTD的1／6，然而需要说明的是，ADI系列方法是时间无条件稳定性方法，也即是说，无论时间步长设置多大，模拟的结果都不会发散，但是并不能保证正确。实际上时间对波形的采样需要满足抽样定理，即时间步长必须要小于关心频段中的最小周期的一半。考虑到计算精度的影响，固定空间步长的情况下，约束条件参数α的取值介于2～5之间较为合适。在存在强反射（散射）的条件下，参数的取值不宜取得太大，而对于弱反射（散射）时，参数的取值则较为宽松，计算效率也将更高。

［1］TAFLOVE A.Computational Electrodynamics：The Finite Difference Time Domain method［M］.Boston：Artech House，2000.

［2］NAMIKI T.A new FDTD algorithm based on alternating－direction implicit method［J］.IEEE Trans.on MTT.，1999，47（10）：2003－2007.

［3］NAMIKI T.3－D ADI－FDTD method unconditionally stable time－domain algorithm for solving full vector Maxwell＇s equations［J］.IEEE Trans.on AP.，2000，48（10）：1743－1748.

［4］ROUF H K，COSTEN F，and GARCIA S G.Reduction of numberical errors in frequency dependent ADIFDTD［J］.Electronics Letters，2010，46（7）：489－490.

［5］SINGH V，AJEET A，KWATRA N，et al.Computation of induced current densities in the human body at low frequencies due to contact electrodes using the ADI－FDTD method［J］.IEEE Trans.EMC，2010，52（3）：537－544.

［6］Pereda J A，Grande A，Gonza？lez O，et al.The ADI－FDTD method for transverse magnetic waves in conductive materials［J］.IEEE Trans.AP.，2010，58（8）：2790－2793.

［7］刘 波，高本庆，薛正辉，等.无条件稳定的交替方向隐式FDTD算法［J］.电波科学学报，2002，17（2）：437－440.LIU Bo，GAO Benqing，XUE Zhenghui，et al.Numerical simulation of unc0nditi0nany stable ADI＿FDTD algorithm［J］.Chinese Journal of Radio Science，2002，17（2）：437－440.（in Chinese）

［8］汤 炜，焦培南，李清亮，等.ADI－FDTD方法在一维PBG结构中的应用［J］.电波科学学报，2003，18（3）：281－285 TANG Wei，JIAO Peinan，LI Qingliang，et al.Application ADI－FDTD in one－dimension PBG structure［J］.Chinese Journal of Radio Science，2003，18（3）：281－285.（in Chinese）

［9］汤 炜，李清亮，焦培南，等.ADI－FDTD在二维散射问题中的应用［J］.电波科学学报，2003，18（6）：620－624.TANG Wei，LI Qingliang，JIAO Peinan，et al.Twodimension scattering analysis using ADI－FDTD method［J］.Chinese Journal of Radio Science，2003，18（6）：620－624.（in Chinese）

［10］张 岩，吕善伟.ADI－FDTD＋GRT在波导电路分析中的应用［J］.电子学报，2005，33（9）：1688－1690.ZHANG Yan，LV Shanwei.Analysis of waveguide circuits using the ADI－FDTD＋GRT method［J］.Acta Electronica Sinica，2005，33（9）：1688－1690.（in Chinese）

［11］郑奎松，葛德彪.总场－散射场方法在二维 ADIFDTD中的实现［J］.西安电子科技大学学报，2006，33（2）：201－210.ZHENG Kuisong，GE Debiao.Imaplementation of the total－field／scattered－field technique in the 2D ADI－FDTD［J］.Journal Xidian University，2006，33（2）：201－210（in Chinese）

［12］汤 炜，闫玉波，李清亮，等.一种新时域交替隐式差分算法在散射问题中的应用［J］.物理学报，2004，53（12）：4173－4179.TANG Wei，YAN Yubo，LI Qingliang，et al.A new ADI－FDTD analysis in electromagnetic scattering［J］.Acta Physica Sinica，2004，53（12）：4173－4179.（in Chinese）

［13］KELLEY D F and LUEBBERS R J.Piecewise linear recursive convolution for dispersive media using FDTD［J］.IEEE Trans.on AP，1993，41（11）：1249－1257.

［14］SULLIVAN D M.Frequency－dependent FDTD methods using Z transform［J］.IEEE Trans.on AP，1990，40（10）：1223－1230.

［15］OKONIEWSKI M，MROZOWSKI M and STUDHLY M A.Simple treatment of multi－term dispersion in FDTD［J］.IEEE Microwave Guided Wave Lett.，1997，7（5）：121－123.

［16］KELLEY D F，LUEBBERS R J.Piecewise linear recursive convolution for dispersive media using FDTD［J］.IEEE.Trans.AP，1996，44（6）：792－797.

［17］魏 兵.各向异性介质电磁散射及参数反演研究［D］.西安电子科技大学，2003.WEI Bin.Study of Electromagnetic Scattering and Reconstruction for Anisotropic Media［D］.Xidian U－niversity，2003.（in Chinese）