鱼骨天线集合线建模对计算结果的影响研究

辛 琦 邹艳林 张福顺 刘其中

（西安电子科技大学天线与微波技术国家重点实验室，陕西 西安710071）

1.引 言

随着通信技术的发展，短波通信系统广泛采用了跳频、扩频等技术，这无疑对天线提出了宽频带工作的要求。鱼骨天线是一种行波宽带天线，具有方向性强、副瓣小且少的优点，常用作短波收信天线，具有良好的抗干扰特性。目前，通常所用的鱼骨天线工作范围一般为6～24MHz，虽然带宽相对较宽，但有时无法满足某些短波全频段通信的需求。因此，对鱼骨天线进行优化设计，使之在短波全频段具有较好的接收性能，是一项亟待展开的工作。

进行优化设计的前提是对天线进行准确的计算，以确保优化的有效性。准确的电磁建模能使计算结果真实反映天线的实际性能，从而达到有效设计的目标。在对鱼骨天线进行分析计算时，除了要考虑天线材料特性、架设区域地形地貌及土壤特性等实际情况［1］外，天线集合线的建模方式对计算结果的影响也是不容忽略的。对天线集合线的建模方式一般有两种，一种是按网络建模，即把集合线等效为无辐射网络。用等效网络思想建模，免去了对集合线具体结构的考虑，易于实现，且可以提高计算速度，降低内存要求，但忽略了集合线的辐射作用及集合线与振子间的耦合作用。另一种是按导线建模，即对工程中所采用的集合线根据其实际结构完全按导线处理。这两种集合线建模方式均被研究者们广泛采用，一般情况下，两者的计算结果差别很小。但我们在研究中发现，对鱼骨天线进行计算时，采用这两种建模方式所得到的天线电性能参数在某些情况下差别较大。因此，有必要研究集合线的建模方式对计算结果的影响，进而选择合适的建模方式，以确保有效地设计工作于短波全频段、性能优越的鱼骨天线。采用矩量法对鱼骨天线分别用上述两种集合线建模方式进行仿真计算，对其结果进行了比较研究，并分析了集合线对天线辐射特性的影响。

2.天线及集合线结构

如图1所示，鱼骨天线由多个等间距对称振子构成，并通过耦合元件接到集合线上，集合线的始端与接收机相连，末端连接与其特性阻抗相等的吸收电阻。鱼骨天线的工作原理是利用水平放置的对称振子接收水平极化波，当电波由集合线的末端到始端方向传播时，所有振子在接收机输入端所产生的电流接近同相，反之当电波由集合线的始端到末端方向传播时接收机端所产生的电流相差最大，这便使鱼骨天线具有单向接收的特性。

图1 鱼骨天线结构示意图

以常用的电阻耦合为研究对象，鱼骨天线的耦合器件通常有电阻、电容或电感，由于集合线的特性阻抗影响到振子的效率和增益，天线增益随集合线特性阻抗的降低而增大［2］。为降低集合线的特性阻抗，同时兼顾工程施工的复杂度，实际中常采用交叉四线式的集合线，其截面图如图2所示，其特性阻抗W 可由式（1）［3］计算。

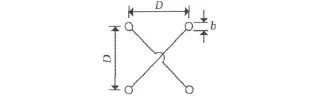
图2 交叉四线集合线截面图

3.矩量法建模

矩量法作为一种有效的数值计算方法，广泛应用于各类复杂电磁计算中［4］，实践证明其计算结果精度较高。

3.1 电流积分方程

对于自由空间的线天线，天线电流所产生的电场分量可以用Pocklington积分方程表示，即

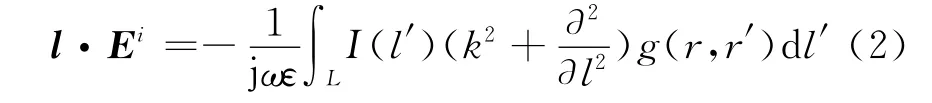
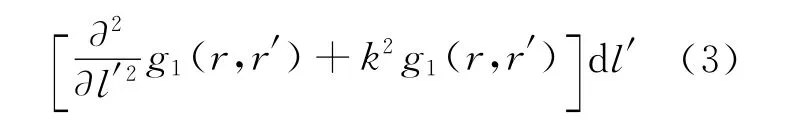
式中：g1（r，r′）＝g（r，r′）＋SI（r，r′），SI（r，r′）为sommerfeld积分［5］，可用平面波反射系数法求得［6］。再用矩量法求解积分方程（3）即可求得天线的电流分布，进而求出天线的电特性。

3.2 基函数

用矩量法求解时，基函数的选取对计算精度和求解效率起着非常重要的作用，在线天线的矩量法分析中采用正弦插值基函数能得到较快的收敛速度［6］。用正弦插值基函数将电流展开为

式中：基函数

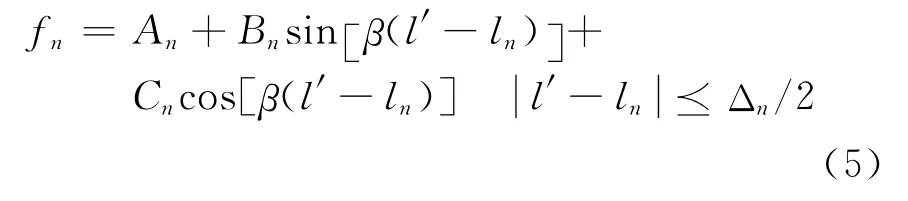
其中，ln表示第n段的中点坐标，Δn为分段长度。三个未知量An，Bn，Cn中，两个可以通过电流、电荷连续性方程确定；另外一个作为矩量法待求变量［7］。将式（4）代入积分方程可得矩阵方程U＝ZI，Z为广义阻抗矩阵。

对于导线段上存在多线节点的情况，如图3所示，在第i段上的基函数延伸到所有与该段相连的各段上，并且在这些段的外侧趋于零且导数为零。因此，其形式可以认为是广义B－样条函数，第i段中心的基函数表示为［6］

图3 含多线节点的导线段

式中：

表示i段上的电流；

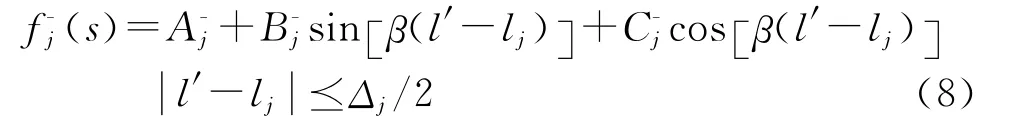
表示第i段的1端连接的导线段电流；

表示第i段的2端连接的导线段电流。

式（6）中一共包含3（N－＋N＋＋1）个系数，但其中只有一个系数不能通过在导线段末端对电流及其导数加边界条件消去，而这个系数可通过解矩阵方程得到。

3.3 广义阻抗矩阵

鱼骨天线是集总参数元件加载的天线，且加载长度比天线长度小得多，流过加载元件Zt上的电流产生的压降为ZtIt，则其广义阻抗矩阵元素应在未加载天线的广义阻抗矩阵基础上修正为［8］

可以看出，当第t段上加载阻抗Zt时，只需将未加载情况下的阻抗矩阵的第t行第t列元素加上Zt即可。求解阻抗矩阵时可采用Z矩阵插值等方法［9］提高计算速度。

3.4 集合线模型

在采用矩量法计算天线特性时，对集合线通常有两种建模方法。

1）按网络建模

按网络建模，就是用等效网络的方法［10］，即把天线看成两个N端口网络的并联，一个网络包括互相耦合的N个振子，另一个网络包括连接振子的集合线。利用电路理论可以得到鱼骨天线各振子输入端等效阻抗方程为

式中：UA、IA为各振子单元输入端的电压和电流矩阵；ZA为振子输入端口阻抗矩阵。

集合线端口处的阻抗方程为

Ul、Il为集合线各端口的电压和电流矩阵，且Ul＝UA；Zl为集合线的阻抗矩阵，它取决于集合线的特性阻抗和间距，其值可以根据传输线理论求得。端口总的电流矩阵可表示为

由I＝［Iin，0，0…0］，可以求出UA，从而求出矩量法中的U，进而求得振子上的电流分布，得到天线特性。

该方法把集合线作为无辐射网络处理，计算天线时没有考虑到集合线的影响。

2）按导线建模

按导线建模，就是在矩量法的求解过程中，把集合线按其实际结构和尺寸，与天线振子一起当导线处理，即对如图2所示的交叉四线集合线按实际结构建模，然后用矩量法求得整个天线（包括集合线）的电流分布，再计算天线的电特性。

4.仿真结果分析

鱼骨天线各振子是通过集合线进行馈电的，在进行天线分析计算时对集合线的处理方式会影响计算结果。为了得到更接近实际情况的准确计算结果，以确保后续优化设计的有效性，用矩量法对鱼骨天线分别按上述两种集合线建模方式进行仿真计算，并分析研究其结果。

以架设于干燥土壤地面上方的定型鱼骨天线为分析目标展开研究。干燥土壤的电参数典型值为：相对介电常数εr＝5，电导率σ＝0.001。常用定型鱼骨天线的结构参数为：振子数目21对，振子臂长8m，振子间距4.4m，耦合电阻180Ω，天线架高17m.四线交叉集合线的典型参数为D＝0.035m和b＝0.003m.分别采用两种集合线建模方式计算了天线在2～30MHz频段的电特性，结果表明该天线在6～24MHz频段内性能良好。

图4 不同频率垂直面方向图（－按导线建模，…按网络建模）

图4、图5给出了不同频点上按两种建模方法计算得到的方向图。可以看出，在低频端，两种建模方法得到的副瓣差别很大。例如3MHz的水平面方向图，考虑集合线影响的方向图后瓣很小，而按照网络建模计算得到的方向图后瓣较大。随着频率的升高，到10MHz左右，两种建模方法得到的结果逐渐接近，而当频率继续升高，副瓣的差别又变得较为明显。其主要原因是集合线的网络建模法没有考虑集合线与振子之间的耦合作用，集合线对电流相位的影响无法体现。在鱼骨天线的低频端和高频端，由于集合线对电流相位的影响，天线满足强方向性的相位条件，后向副瓣较小，即此时集合线对天线辐射方向的影响很大，所以两种建模方式得到的方向图差异就较大。

图5 不同频率水平面方向图（－按导线建模，…按网络建模）

用两种建模方法计算得到的最大增益、垂直面最大辐射仰角如表1所示，效率如图6所示。从表1可以看出，按网络建模计算出的仰角在某些频点较按导线建模的结果低1～4度；按网络建模得到的增益总体低于按导线建模得到的增益，在个别频点高于按导线建模的结果。对于天线效率，两者的结果曲线变化趋势基本一致，但按导线建模计算得到的效率比较低，这是由于考虑了集合线的影响，而使天线辐射电阻大大降低的缘故。

图6 效率结果对比

由图7，图8可以看出按等效网络建模计算出的输入阻抗起伏比较大，而按照导线建模得到的输入阻抗变化比较平缓，这与天线的实际应用情况是一致的，说明根据集合线的实际结构按导线建模得到的结果更接近实际情况。

表1 增益和最大辐射仰角结果对比

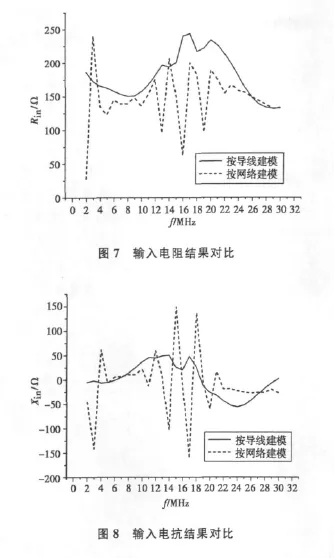
以上结果及分析表明鱼骨天线的集合线对天线辐射特性的影响是比较大的，如果按照网络建模忽略集合线影响，则计算结果在多数频点与实际的误差会较大。因此，对于短波宽频带鱼骨天线的分析与优化设计，采用集合线按导线建模的方式比较合适。

5.结 论

集合线作为鱼骨天线的馈电线，是天线的重要组成部分，对集合线建模通常可采用按网络和按导线两种方式。本文分别按照这两种集合线建模方式对鱼骨天线进行了仿真计算，并对其结果展开了对比研究，分析了集合线对天线辐射特性的影响。在低频和高频端，考虑集合线影响按导线建模得到的方向图后向副瓣很小，而按网络建模不考虑集合线的影响时，得到的后向副瓣较大。按网络建模得到的输入阻抗变化起伏较大，按导线建模得到的输入阻抗变化比较平缓。按照两种建模方式计算得到的增益、垂直面最大辐射仰角以及效率也都存在不同程度的差异。两者计算结果的差异说明鱼骨天线集合线的建模方式对天线性能的计算结果影响较大。在分析和设计短波全频段、性能优越的鱼骨天线时，为了确保设计的有效性，对集合线采用更接近实际情况的导线建模方式比较合适。

［1］张志刚，郑龙根，王跃平，等.远距离短波鱼骨天线的仿真设计［J］.电波科学学报，2009，24（2）：332－336.ZHANG Zhigang，ZHENG Longgen，WANG Yueping，et al.Simulation and design of long－distance HF fishbone antenna［J］.Chinese Journal of Radio Science，2009，24（2）：332－336.（in Chinese）

［2］爱金堡.短波天线［M］.北京：人民邮电出版社，1965.

［3］李小曼.短波天线维护手册［M］.北京：人民邮电出版社，1991.

［4］HARRINGTON R F.Field Computation by Moment Methods［M］.New York：Macmillan，1968.

［5］孙学军，金元松，刘玉龙，等.Sommerfeld型广义积分和近距离地面场强［J］.电波科学学报，2008，23（2）：216－220.SUN Xuejun，JIN Yuansong，LIU Yulong，et al.Approximation expression of ground wave field intensity at short range from the vertical element over the flat earth［J］.Chinese Journal of Radio Science，2008，23（2）：216－220.（in Chinese）

［6］BURKE G J and POGGIO A J.Numerical Electromagnetic Code （NEC2）－Method of Moments［R］.Rep UCID 18834，Lawrence Livermore Laboratory，CA，1981.

［7］孙保华.VHF／UHF全向宽带小型化天线的研究［D］.西安电子科技大学，2001.SUN Baohua.Analysis and Optimal Design of Broadband Omnidirectional Miniaturized VHF／UHF Antennas［D］.Xidain University，2001.（in Chinese）

［8］延晓荣，金元松，罗翠梅.阻容加载偶极天线的宽带性能及效率分析［J］.电波科学学报，2000，15（2）：169－173.YAN Xiaorong，JIN Yuansong，LUO Cuimei.Analysis of wide－band properties and efficiency for dipole antennas with resistive and capacitive loadings［J］.Chinese Journal of Radio Science，2000，15（2）：169－173.（in Chinese）

［9］孙保华，刘其中.采用Z矩阵插值法快速计算套筒单极子天线［J］.西安电子科技大学学报，2001，28（1）：125－128.SUN Baohua，LIU Qizhong.Rapid calculation of skirt monopole antenna by Z matrix interpolation method［J］.Journal of Xidain University，2001，28（1）：125－128.（in Chinese）

［10］李世智.电磁辐射与散射问题的矩量法［M］.北京：电子工业出版社，1985.