沥青混凝土弯曲疲劳试验疲劳损伤分析

周志刚，张清平，袁秀湘

(长沙理工大学 道路结构与材料交通行业重点实验室，湖南 长沙，410004)

沥青路面的疲劳性能是表征沥青路面耐久性的重要性质之一。鉴于沥青混合料以及路面结构的疲劳破坏实质上是材料局部出现劣化损伤并逐渐扩展、发展成为裂缝直至断裂破坏的过程，为此，需要在试验基础上进一步应用疲劳损伤力学理论与方法揭示材料及结构疲劳损伤破坏的演化过程，认识疲劳破坏的机制。关于沥青混合料疲劳损伤，一般基于2类损伤理论，即弹性损伤理论[1-5]和黏弹性损伤理论[6-11]。这些研究中尽管应用损伤力学理论与方法，但损伤值一般用试件的刚度或模量的变化来定义，该参量具有平均意义，并不能真实地反映试件局部损伤及其发展过程。例如弯曲疲劳试验研究中采用根据梁式试件挠度与弯矩计算得到的截面等效弯曲刚度来定义计算梁的损伤值，显然，这表示梁在整个截面平均的损伤值，忽视了同一断面上不同受力状态区域损伤的差异性，由此得到的疲劳损伤演化关系及其有关参数不能真实地反映材料微观损伤特性及其损伤演化过程。其原因主要是：在这些试验中，未能获取试件局部应变、微观结构变化等与经典损伤定义直接相关的信息。为此，本文作者结合沥青混凝土梁式试件弯曲疲劳试验，采用反分析的方式，以提出真实体现沥青混合料损伤演化的模型。其步骤是：首先提出沥青混合料的非线性疲劳损伤演化模型；然后，应用解析与数值仿真分析的方法演绎疲劳试验过程，将所得结果与疲劳试验结果进行对比，以论证模型的合理性和有效性。

1 梁式试件疲劳损伤力学理论的经典解

1.1 疲劳损伤方程

由于一般疲劳试验过程只采集循环荷载及其次数、梁的挠度等，而无法直接获取损伤信息，故采用以下非线性疲劳损伤演化方程[12]来进行反分析：

式中：a*，p和 q为材料的损伤特性参数，与载荷循环特征R及温度T有关；损伤变量D采用Kachanov的经典定义，将经典的弹性损伤本构方程 σ=E(1-D)ε代入式(1)，并令a=a*Ep，有：

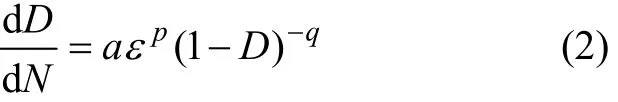
1.2 梁式试件的拉压分区及有关力学量计算

假定沥青混合料梁式试件损伤前拉压弹性模量没有区别，即具有各向同性性质，但由于其损伤破坏体现为拉伸形式，故出现在梁式试件的受拉一侧。假定受压一侧不会出现因损伤引起的力学性质的变化，故沥青混合料梁式试件x断面的拉压分界点z0(x)由断面轴向受力平衡确定：

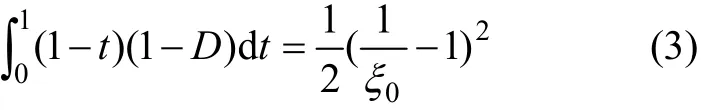
其中：ξ=z/h；ξ0=z0(x)/h；t=ξ/ξ0；dξ=ξ0dt。

x断面内的拉压应力可按下式计算：

在受拉区，

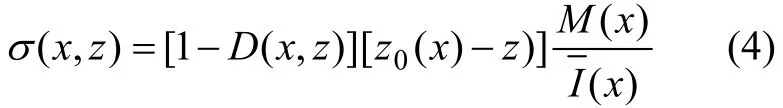
在受压区，

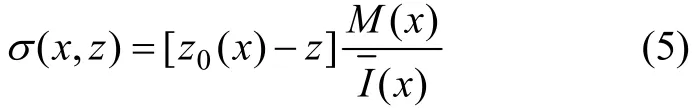
其中：E I (x)为材料损伤后 x断面的等效弯曲刚度；I( x)为x断面的等效惯性矩。

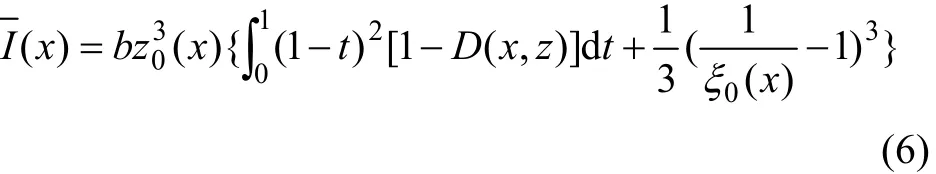
x断面内受拉区任一点的损伤值可根据最危险点M的损伤值进行计算：

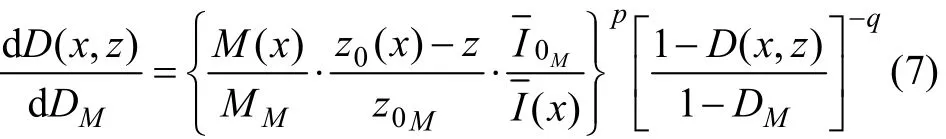
1.3 疲劳裂纹形成与扩展的疲劳寿命

1.3.1 疲劳裂纹形成阶段的疲劳寿命

试件未断裂前以 M点表示最危险断面(梁跨中断面)内受拉区距中性轴最远的点(试件表面)，εM和 DM分别表示 M 点的正应变幅值与损伤值。由式(2)，M点达到损伤值 DM时的疲劳寿命(疲劳裂纹形成寿命)Ncr为：

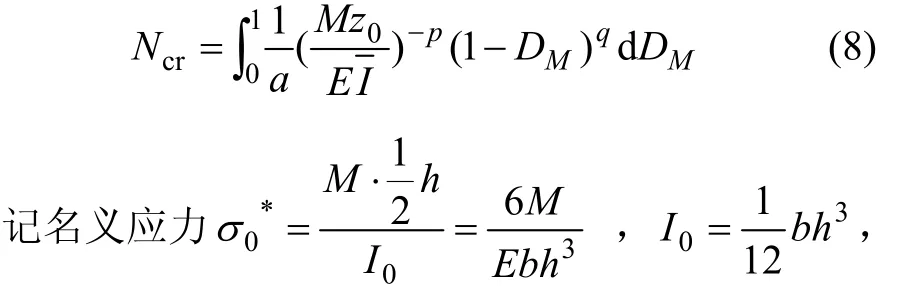
则

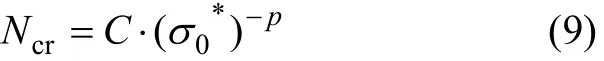
其中：

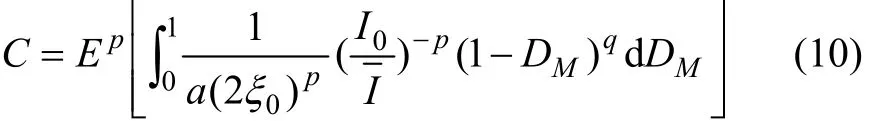
材料特性损伤参数a与荷载、损伤无关，从而，

其中：

计算疲劳裂纹形成阶段的疲劳寿命的基本步骤见文献[12]。

1.3.2 疲劳裂纹扩展阶段的疲劳寿命

当循环次数达到 Ncr时，疲劳裂纹形成，试件进入疲劳裂纹扩展阶段。采用与疲劳裂纹形成阶段一样的分段方式，即在计算疲劳裂纹扩展阶段的疲劳寿命时，将计算断面等分为m2段(含 m2+1点)，每段长度为 Δh=h/m2。

当循环加载次数N达到Ncr时，试件表面点1的损伤值达到1，此时，相邻点2的损伤值达到随着N进一步增加，点2的损伤值达到=1，产生损伤失效。此时，所对应的循环加载次数增加量为：

其中： z′0为产生裂纹长度a1=z2-z1后试件有效断面内在以点 2为坐标原点的新坐标系下的拉压分界点坐标；I′为此时的等效惯性矩。依此类推，第i-1点失效时，对于第i点，其损伤值为前i-1段开裂过程的累积损伤结果。当其损伤值达到1时，所对应的循环加载增加量为：

疲劳裂纹扩展寿命ΔN与疲劳全寿命Nf分别为：

2 沥青混合料弯曲疲劳试验及疲劳损伤特性参数

采用三点弯曲疲劳试验测试方法。分别选用3种70号沥青制作中粒式密级配矿料沥青混凝土，试件采用轮碾成型后切割成规定尺寸的制作方法。进行疲劳试验时，采用10 Hz的正弦波作为加载波形，加载时间为16 ms，相邻波形间没有间歇时间。

试验所用的3种沥青混凝土的抗弯拉强度和弯拉回弹模量见表1。

根据弯曲疲劳试验结果，疲劳方程N=Cσ-p中的疲劳参数C和p回归值见表2。

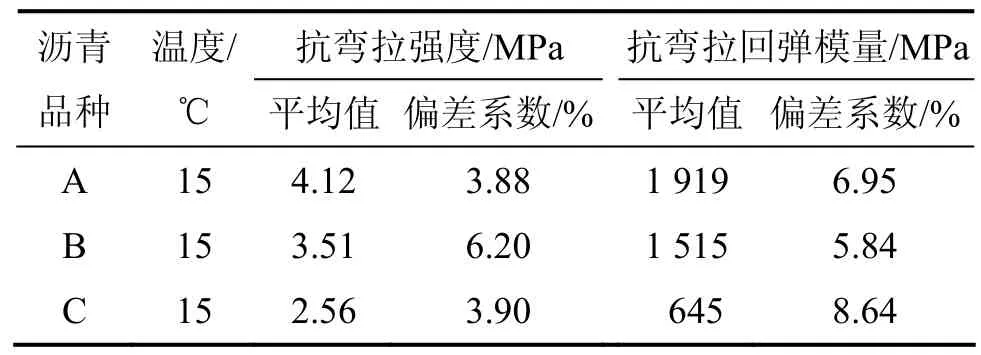
表1 沥青混凝土的抗弯拉强度和弯拉回弹模量Table 1 Bending strenghth and modulus of asphalt mixtures

表2 疲劳试验结果Table 2 Results of fatigue tests

取表2中3种沥青混凝土疲劳试验结果的平均值，即C=40 467，p=3.45。根据疲劳损伤裂纹形成阶段的有关计算及式(11)，得到沥青混凝土疲劳损伤特征参数 a=1.525×10-5。

3 三点弯曲试件疲劳损伤的有限元分析

3.1 疲劳损伤力学-有限元方法

采用平面应变条件下的八节点等参单元有限元方法，考虑损伤时弹性矩阵S为：

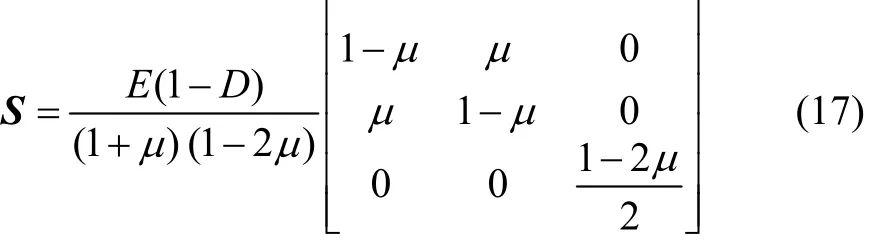
在进行疲劳损伤分析与裂纹形成及扩展寿命预估时，应用文献[13]中所述步骤进行计算。在模拟计算过程中，当某点累积损伤值达到1.0时即认为该点开裂，当连续多点损伤值均达到 1.0时即认为它们形成了1条裂纹。

利用自编的有限元程序计算损伤不同增长步长ΔD为0.01，0.02，0.03，0.04和0.05时的疲劳损伤，结果表明均能取得较高的精度，故本文的有限元计算中，均取ΔD=0.02的增长量步长。

分别取5种集中荷载，使各个荷载初次作用于沥青混合料梁式试件时在其跨中断面底部产生的最大弯拉应力σ0分别为0.4，0.6，0.8，1.0和1.2 MPa。然后，计算分析沥青混合料梁式试件在这5种集中荷载循环作用下的疲劳损伤开裂及其断裂过程，并与经典损伤理论分析和试验结果进行对比。

三点弯曲试件的长×宽×高为 250 mm×30 mm×35 mm，跨中长度为 200 mm。有限元网格划分为756个八节点等参单元，共2 405个节点。

3.2 弯拉应力

3.2.1 梁底面弯拉应力

试件开裂前其底面弯拉应力 σx底分布随疲劳荷载作用的变化曲线见图1。从图1可见：随着疲劳损伤变量 DM的增大，梁式试件底面产生最大弯拉应力的位置逐渐地从跨中向两侧转移；当 DM=1.0时，最大弯拉应力点的位置距跨中M点约为1.0 cm。并且梁式试件底面最大弯拉应力也由 0.40 MPa降低为 0.25 MPa；同时，M点的弯拉应力由最大值逐渐衰减，当DM=1.0时变为0 MPa，见图2。从图2可见：其衰减的速度随损伤变量 DM的增大而加快；此外，对于跨中M点的弯拉应力，其有限元计算结果(实线)与经典理论结果(虚线)很接近。

图1 σ0=0.4 MPa时开裂前试件底面弯拉应力分布Fig.1 Distribution of bending stress at specimen bottom before cracking when σ0=0.4 MPa

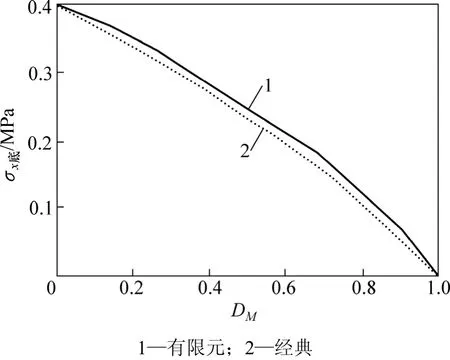
图2 σ0=0.4 MPa时试件跨中M点弯拉应力随损伤的变化Fig.2 Variation of M point’s bending stress with damage in specimen middle when σ0=0.4 MPa

当开裂以后，随着裂纹长度的增加，梁底面最大弯拉应力点位置继续向两侧转移，最大弯拉应力有所降低，见图3。并且裂缝附近弯拉应力零值区稍扩大。

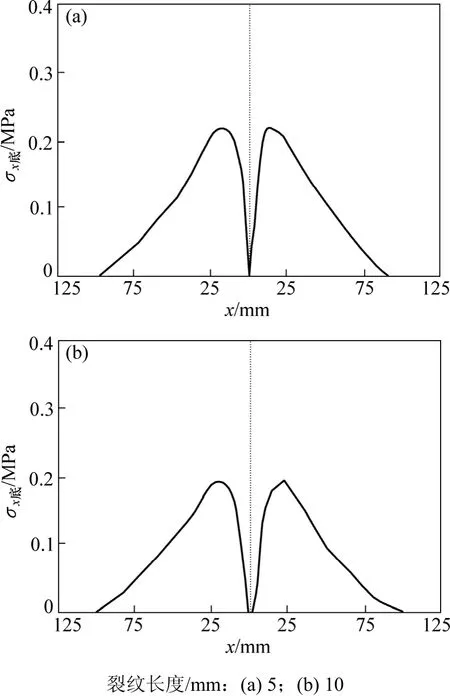
图3 开裂后试件底面弯拉应力分布(σ0=0.4 MPa)Fig.3 Distribution of bending stress at specimen bottom after cracking (σ0=0.4 MPa)

3.2.2 跨中断面弯拉应力

在出现损伤前，跨中断面大部分截面弯拉应力几乎呈线性，只是在梁式试件顶面集中荷载作用区附近出现异常现象，即压应力急剧增大(见图4)。这与集中荷载区的应力集中现象有关。该影响一直存在于损伤、开裂全过程。随着梁底面产生损伤，M点的弯拉应力逐渐减小，断面上产生最大弯拉应力的位置逐渐向上转移；开裂以后，由于有效断面减小，弯拉刚度降低，在跨中断面上产生的最大弯拉应力和压应力均增大。在裂纹出现、扩展全过程中，拉压分区点位置逐渐向上发展。

图4 跨中断面弯拉应力分布(σ0=0.4 MPa，有限元方法)Fig.4 Distribution of bending stress along cross section of specimen middle(σ0=0.4 MPa, FEM)

跨中断面弯拉应力经典理论值见图 5。对比图 4和图5可见：经典损伤理论解与有限元方法计算结果较接近，主要差别在于集中荷载附近受压区的应力分布。由于经典损伤理论解未考虑集中荷载附近应力集中，故该受压区应力与有限元结算结果相差较大。

3.3 梁的挠度

图5 跨中断面弯拉应力分布(σ0=0.4 MPa，经典损伤理论解)Fig.5 Distribution of bending stress along cross section of specimen middle (σ0=0.4 MPa, Classic theorical solution)

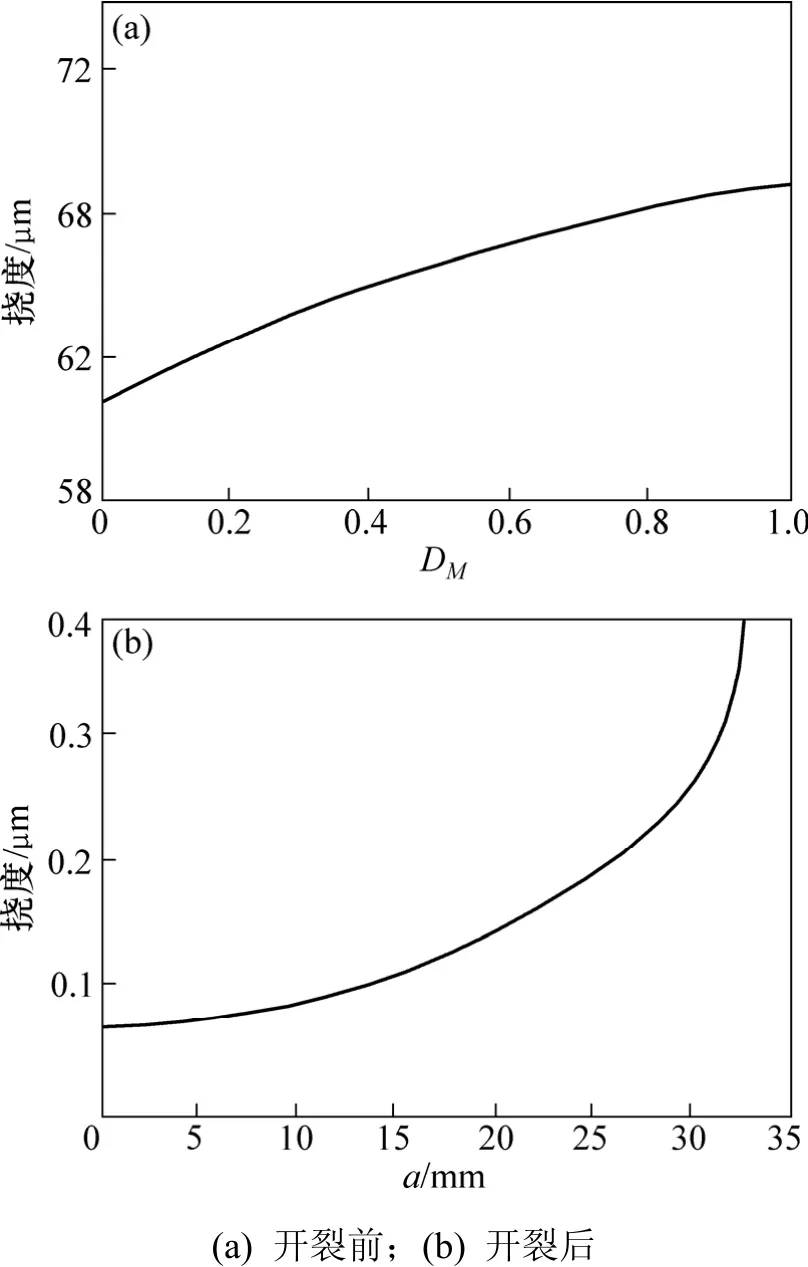
图6 σ0=0.4 MPa时跨中挠度随损伤、开裂的变化Fig.6 Variation of deflection in specimen middle with damage and cracking when σ0=0.4 MPa

在梁底面开裂前，梁的跨中挠度V随着疲劳损伤的发展而增大，但增大的速度逐渐趋缓(见图6(a))。这是由于梁开始出现损伤时，损伤区主要在跨中，对该处弯拉刚度影响较大；随着损伤的进一步加深，损伤区范围扩大，受损区弯拉刚度降低对梁跨中挠度的影响趋于平缓。

当梁底面开裂后，跨中挠度随着裂纹的扩展增大，且增大的趋势逐渐加剧，当裂纹长度达到 25～30 mm时，出现失稳断裂(见图6(b))。

3.4 损伤变量

开裂前损伤区主要位于梁底部和跨中两侧，损伤最大的位于跨中底，将从此处产生疲劳裂纹(见图7)。起裂后，疲劳裂纹持续沿着跨中断面向上发展(见图8)。

图7 σ0=0.4 MPa时开裂前损伤场Fig.7 Distribution of damage before cracking when σ0=0.4 MPa

图8 σ0=0.4 MPa和a=20 mm时开裂后损伤场Fig.8 Distribution of damage after cracking when σ0=0.4 MPa and a=20 mm

在梁上部及支点之间存在着大片无损和轻微损伤区域，这是由于在疲劳损伤中只考虑了受拉和剪切损伤，认为受压不会引起损伤。

3.5 疲劳损伤寿命

在梁式试件底面开裂前，根据有限元方法计算结果绘制的疲劳曲线(即疲劳寿命与作用荷载应力关系曲线)与试验曲线非常接近(见图 9)。有限元方法与试验回归所得疲劳寿命见表3。由表3可见：二者最大误差在17.7%以内；而疲劳寿命预估误差在30%以内，均是可以接受的。

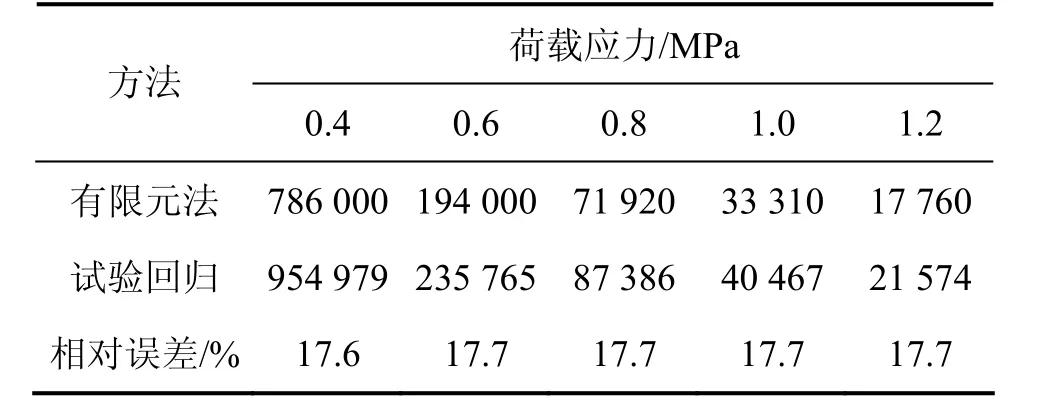
表3 有限元方法与试验回归的疲劳寿命比较Table 3 Comparing the theoritical fatigue lives with experimental results

当梁式试件底面开裂后，在同一裂纹长度时，荷载应力大，则疲劳寿命短；当裂纹长度达到约20 mm后，疲劳寿命趋于稳定，即将进入失稳扩展阶段(见图10)。开裂前后疲劳寿命比较结果见表4。由表4可见：结合前面梁的挠度分析，若以裂纹长度为25 mm作为失稳扩展分界，则失稳时的疲劳寿命比产生裂纹时的疲劳寿命延长约0.74倍。

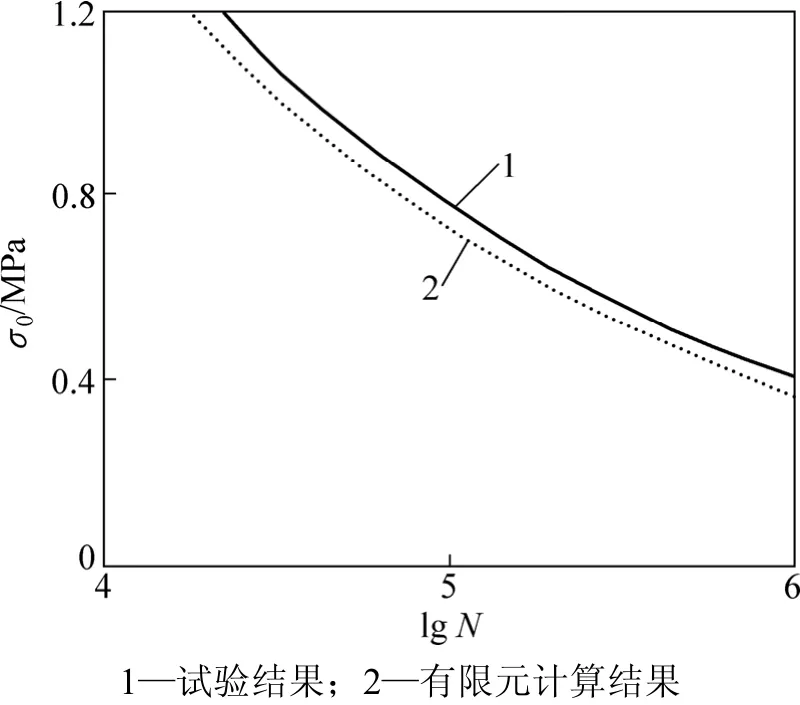
图9 疲劳曲线Fig.9 Fatigue curve

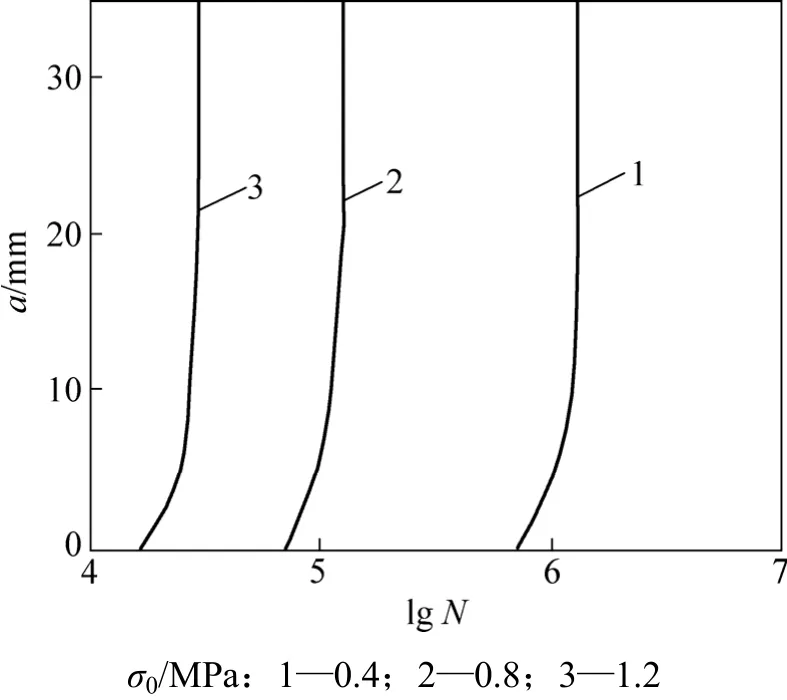
图10 疲劳寿命随裂纹长度的变化Fig.10 Variation of fatigue life with crack length

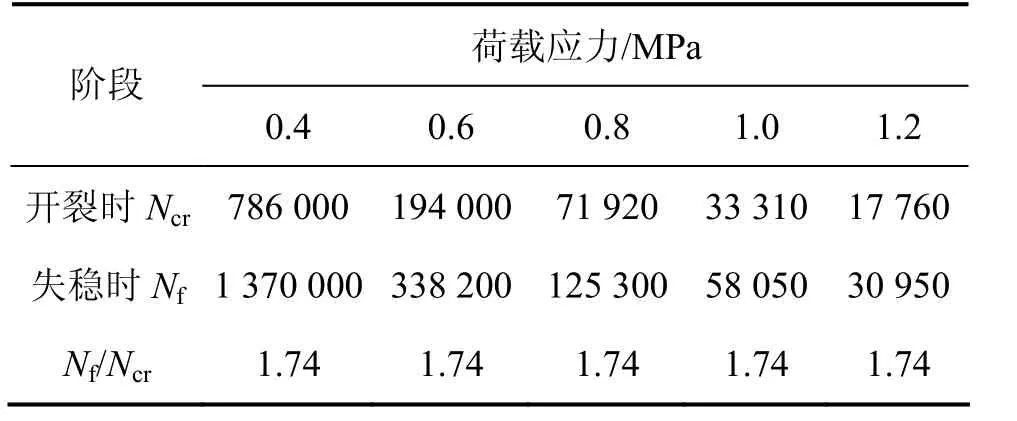
表4 开裂前后疲劳寿命比较Table 4 Comparison of the fatigue lives before cracking and after cracking 次

3.6 裂纹扩展速率

根据不同荷载应力下三点弯曲梁式试件疲劳损伤开裂、断裂过程的有限元计算，可以求出不同荷载应力、不同裂纹长度时的裂纹扩展速率见图11。从图11可见：随着裂纹长度的增大，裂纹扩展速率逐渐加大，当裂纹扩展至20 mm以后呈现出急剧变化趋势。这结果与前面根据梁的挠度、疲劳寿命与裂纹长度关系推测结果相一致。并且对于同一裂纹长度，在荷载应力较大时，其裂纹扩展速率相应增大。

3.7 Paris公式参数

在疲劳裂纹扩展分析中经常采用 Paris公式预测其扩展寿命。针对本文所分析的沥青混合料三点弯曲梁式试件，根据裂纹扩展速率的有限元计算结果，下面计算回归Paris公式中的参数A和m。

其中：da/dN为裂纹扩展速率，mm/次；K为应力强度因子， MPa·mm1/2。

为此，首先根据文献[14]提供的公式，计算各个荷载应力下不同裂纹长度时的I型应力强度因子K：

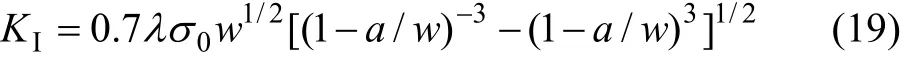
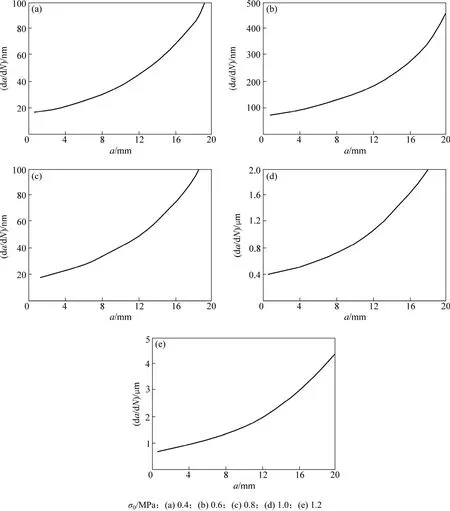
图11 裂纹扩展速率与裂纹长度关系Fig.11 Relationship between crack expanding velocity and crack length

其中：a为裂纹长度；w为梁式试件高度；σ0为荷载应力。

裂纹扩展速率和应力强度因子关系曲线见图12。从图12可见：当产生裂纹后，初始阶段裂纹扩展速度较小；当裂纹长度发展到6.25 mm后，进入稳定扩展阶段；当裂纹长度接近20 mm时，裂纹扩展速度加快，将进入失稳扩展阶段。由于Paris公式是反映稳定扩展阶段的疲劳裂纹扩展规律，因此，在采用双对数坐标下的最小二乘法回归(Paris公式，式(18))中疲劳断裂参数时，剔除裂纹长度大于20 mm的点。回归结果为：A=1.832×10-5，m=1.938；相关系数为0.870。若剔除裂纹扩展初始阶段和20 mm附近少量点，则可以获得相关性更强的回归结果。

疲劳裂纹扩散速率与应力强度因子的关系见图12。从图12可见：在稳定扩展阶段，裂纹扩展速率与应力强度因子具有良好的双对数线性关系，可以采用Paris公式预测裂纹扩展寿命。

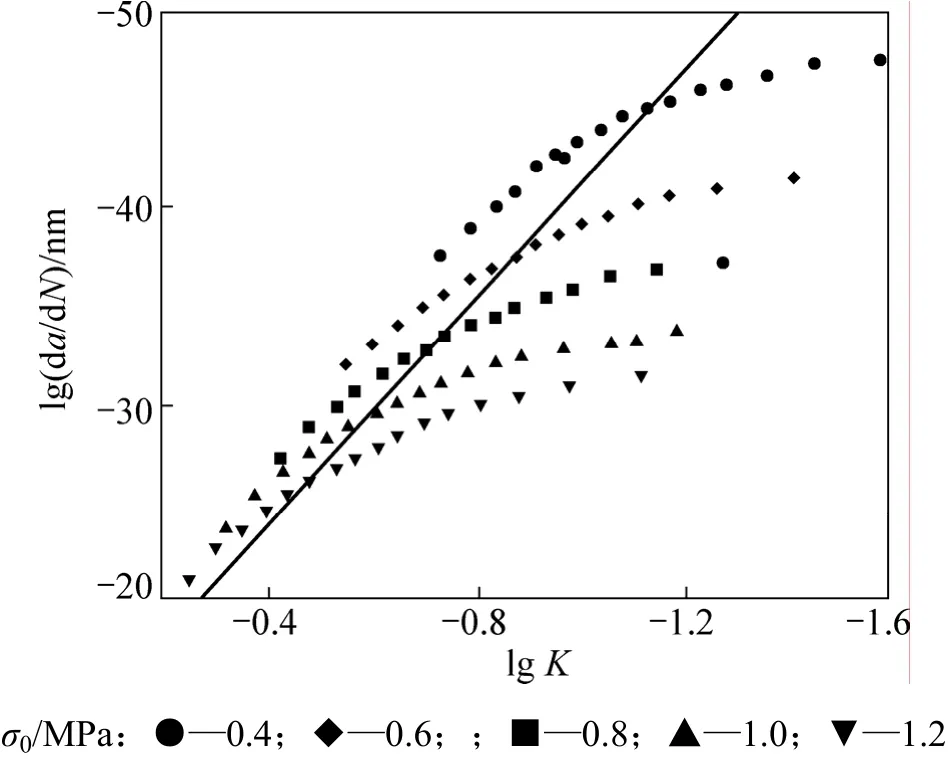
图12 疲劳裂纹扩展速率与应力强度因子的关系Fig.12 Relationship between fatigue crack expanding velocity and stress strenghth index

4 结论

(1) 根据疲劳损伤力学理论，推导出疲劳过程中三点弯曲梁试件内部应力、损伤场等随荷载循环次数的演化方程，以及疲劳裂纹形成阶段和扩展阶段疲劳寿命公式。并根据疲劳试验数据得到了沥青混凝土材料疲劳损伤模型中的特征参数。

(2) 应用疲劳损伤力学有限元方法,模拟计算了三点弯曲梁疲劳损伤断裂过程，分析了试件疲劳损伤过程中的弯拉应力、跨中位移、损伤变量、裂纹扩展速率等的变化规律，并预测了沥青混合料试件失稳断裂时的裂纹长度。疲劳寿命的数值模拟结果与试验结果较吻合，证明了在梁式试件三点弯曲疲劳试验情况下所提出的沥青混合料疲劳损伤模型的合理性和有效性。

(3) 对于三点弯曲梁试件，其疲劳裂纹扩展阶段的疲劳寿命比形成阶段的疲劳寿命短；疲劳裂纹扩展主要表现为稳定扩展，可以运用Paris公式描述疲劳裂纹扩展阶段，并回归得到了有关的疲劳断裂参数。

[1] 葛折圣, 黄晓明. 运用损伤力学理论预测沥青混合料的疲劳性能[J]. 交通运输工程学报, 2003, 3(1): 40-42.GE Zhe-sheng, HUANG Xian-ming. Prediction of asphalt mixtures fatigue properties using damage mechanics[J]. Journal of Traffic and Transportation Engineering, 2003, 3(1): 40-42.

[2] 朱洪洲, 黄晓明. 一种新的沥青混合料疲劳性能评价方法[J].公路交通科技, 2005, 22(2): 5-7.ZHU Hong-zhou, HUANG Xiao-ming. Fatigue model of asphlat mixtures based on damage theory[J]. Journal of Highway and Transportation Research and Development, 2005, 22(2): 5-7.

[3] 仰建岗, 王秉纲, 陈拴发. 基于修正 Neuber方程的沥青路面裂缝形成疲劳寿命预估方法[J]. 交通运输工程学报, 2007,7(2): 50-54.YANG Jian-gang, WANG Bing-gang, CHEN Shuan-fa.Estimating method of fatigue life during cracking initiation of asphalt pavement based on modified Neuber equation[J]. Journal of Traffic and Transportation Engineering, 2007, 7(2): 50-54.

[4] 吴旷怀, 张肖宁. 沥青混合料疲劳损伤非线性演化统一模型试验研究[J]. 公路, 2007, 5: 125-129.WU Kuang-huai, ZHANG Xiao-nin. Experimental research on uniform model for nonlinear evolution equation of fatigue damage of asphalt mixture[J]. Highway, 2007, 5: 125-129.

[5] 郑健龙, 吕松涛. 沥青混合料非线性疲劳损伤模型[J]. 中国公路学报, 2009, 22(5): 21-27.ZHENG Jian-long, LU Song-tao. Nonlinear fatigue damage model for asphalt mixtures[J]. China Journal of Highway and Transport, 2009, 22(5): 21-27.

[6] 周晓青, 李宇峙, 应荣华, 等. 沥青混合料拉伸疲劳试验下疲劳损伤特性研究[J]. 重庆建筑大学学报, 2005, 27(5): 47-51.ZHOU Xiao-qing, LI Yu-zhi, YING Rong-hua, et al. Research on the fatigue and damage characteristics of asphalt mixture based on uni-axial fatigue tension testing at low temperature[J].Journal of Chongqing Jianzhu University, 2005, 27(5): 47-51.

[7] 应荣华, 陈晓, 张志勇. SBS改性沥青混合料损伤模型分析[J].长沙交通学院学报, 2006, 22(1): 42-47.YING Rong-hua, CHEN Xiao, ZHANG Zhi-yong. Damage model analysis of sbs modified asphalt mixture[J]. Journal of Changsha Communications University, 2006, 22(1): 42-47.

[8] Castro M, Sanchez J A. Damage based model for prediction of asphalt concrete fatigue curves[J]. J Mat in Civ Engrg, 2007,19(8): 700-702.

[9] 关宏信, 郑健龙, 张起森. 沥青混合料的粘弹性疲劳损伤模型研究[J]. 力学与实践, 2007, 29(2): 50-53.GUAN Hong-xin, ZHENG Jian-long, ZHANG Qi-sen.Viscoelastic fatigue damage model of bituminous mixture[J].Mechanics in Engineering, 2007, 29(2): 50-53.

[10] 吴旷怀, 杨国良, 张肖宁. 考虑松弛的沥青混合料疲劳损伤累计模型研究[J]. 深圳大学学报, 2008, 25(4): 345-350.WU Kuang-huai, YANG Guo-1ian, ZHANG Xiao-nin. A fatigue damage model of asphalt mixture considering stress relaxation[J].Journal of Shenzhen University Science Angineering, 2008,25(4): 345-350.

[11] 关宏信, 郑健龙. 沥青路面粘弹性疲劳损伤分析[J]. 湖南科技大学学报: 自然科学版, 2008, 23(3): 54-57.GUAN Hong-xin, ZHENG Jian-long. The viscoelastic fatigue damage developing of asphalt pavement[J]. Journal of Hunan University of Science & Technology: Natural Science Edition,2008, 23(3): 54-57.

[12] 余寿文, 冯西桥. 损伤力学[M]. 北京: 清华大学出版社, 1997:110-112.YU Shou-wen, FENG Xi-qiao. Damage mechanics[M]. Beijing:Qsinghua University Press, 1997: 110-112.

[13] 周志刚. 交通荷载下沥青类路面疲劳损伤断裂研究[D]. 长沙:中南大学土木建筑学院, 2003: 24-26.ZHOU Zhi-gang. A research on the fatigue damage cracking in asphalt pavement under traffic load[D]. Changsha: Central South University. School of Civil Engineering and Architecture, 2003:24-26.

[14] 杜庆华. 工程力学手册[M]. 北京: 高等教育出版社, 1994:211-212.DU Qing-hua. Engineering mechanics manual[M]. Beijing:Higher Education Press, 1994: 211-212.