一种具有负载平衡的虚拟计算环境拓扑

邓晓衡，张连明，刘毅，赵扶摇, 陈志刚

(1. 中南大学 信息科学与工程学院，湖南 长沙，410083;2. 湖南师范大学 物理与信息科学学院，湖南 长沙，410081)

基于 Internet的虚拟计算环境(Internet based virtual computing environment, iVCE)[1]中的资源、用户具有动态性，一方面，表现在资源、用户加入虚拟计算环境具有动态性；另一方面，虚拟计算环境中在线的资源、用户个体和系统整体网络拓扑也处于一种动态的演化过程中，因此，虚拟计算环境的动态演化对于系统的性能有何影响、如何演化才能促进系统优化，成为互联网环境领域越来越热的研究问题。对Internet以及 Internet上的大型分布式应用系统的分析研究发现，其网络的拓扑结构并不是随机网络，也不是规则网络，而是介于其间的复杂网络[2-4]，网络拓扑结构对于系统的性能具有极其重要的意义。对互联网网络拓扑建模，形成了一些重要拓扑模型(如随机图拓扑模型[5])和基于层次结构的拓扑模型(如 Transit-Stub[6])以及基于节点度的互联网拓扑模型(如 Inet[7]、动态模型BA[8])等。这些研究成果对于探索拓扑特性和拓扑结构等对网络行为以及网络性能的影响，最终改善网络技术、提高网络服务性能以及设计新型基于互联网的应用系统拓扑等均具有重要意义。

1 Gnutella网络拓扑分析

1.1 iVCE与Gnutella

在虚拟计算环境中，资源和用户都被虚拟化成自主元素。自主元素会基于应用的需求，在互联网上搜寻相应的虚拟计算环境，进而根据自己的兴趣需求加入到某一个虚拟共同体中[1]。自主元素也可以作为一个超级自主元素来创建一个虚拟共同体，并发布自己的信息，允许别的用户和资源加入到本虚拟共同体中，其组织结构如图1所示。网络拓扑分为2层：上层主要由超级自主元素组成，下层主要由一般自主元素组成。超级自主元素承担更多的系统管理和通信消息转发功能，普通自主元素则主要发起请求或提供相应的应用服务。

图1 虚拟计算环境服务组织结构Fig.1 Service organizing structure of virtual computing environment

Gnutella是P2P计算的典型代表之一，在互联网上拥有大量的用户，具有广泛的影响。最初的Gnutella协议由于采用扁平的拓扑结构和简单的flooding的资源搜索机制而缺乏扩展性且性能较差；Gnutella2则采用二层覆盖网体系结构，如图2所示。

图2中，少数超级节点(super peers)构成了覆盖网的顶层，super peers相互连接通信，负责消息路由转发；绝大部分是叶子节点(leaf peers)，它们构成底层覆盖网。leaf peer 通过super peer连接到顶层，叶子节点将自己共享内容的哈希值上传到与其连接的超级节点上，不负责查询消息的转发工作；若一个节点没有找到合适的 super peer接入网络，则将其设置变成super peer，其本质仍为一般节点，未实现超级节点功能，不与叶子节点相连，只能与网络中的超级节点建立连接。Gnutella 2采用动态查询的资源搜索方法，当查询请求发出后有足够的合适结果返回，当满足用户需求时，就中止查询过程，在顶层网络中只需很低的TTL(Time-To-Live)即可。由此可见：iVCE和Gnutella的网络拓扑构造具有相似特征，对iVCE的拓扑建模，拟利用当前对Gnutella网络拓扑测量的结果，利用其拓扑结构以其对应的拟合模型对iVCE拓扑结构建模。

图2 Gnutella网络的两层结构Fig.2 Two-tier structure of Gnutella

1.2 Gnutella网络拓扑分析

Gnutella作为P2P应用典型的代表，Jovanovic[9]对早期的Gnutella网络拓扑进行测量，发现Gnutella网络拓扑节点的分布呈现幂律和小世界特性。Stutzbach等[10]针对Gnutella网络的分层特性，构造拓扑爬行器，分析了 Gnutella网络中超级节点(super-peers)、叶子节点(leaf-peers)等度分布特性，指出Gnutella网络节点度分布不服从幂律。刘刚等[11]构造支持Gnutella v0.4协议的拓扑爬行器，分析其拓扑快照，发现Gnutella网络的小世界特性，验证网络中存在度指数幂律特征，王勇等[12]通过设计高效的网络爬虫测量Gnutella的拓扑数据分析发现其拓扑节点度分布呈现分3段幂率分布，拓扑具有小世界网络特性。其拓扑特征总体表现为如下。

(1) 节点度呈多种特征分布。Gnutella网络分为上层/底层2层节点，如图2所示，2层中的节点实现的功能、采取的连边策略各不相同，上层节点的度(Super to super peers)与其降序序列中的等级之间分三段符合幂律分布；网络中超级节点对叶节点度数(Super to leaf peers)与其降序序列中的等级之间分2段符合幂律分布；叶节点连接的超级节点度(Leaf to super peers)与其降序序列中的等级之间分三段符合幂律分布。度的频率分布(Degree-frequency distribution)特征刻画Gnutella网络拓扑度频率分布特性。叶节点到上层节点(Leaf to super peers)连接的度概率分布具有较强的幂律特性；超级节点到叶节点(Super to leaf peers)连接的度概率密度呈“钟型”分布；上层节点之间(Super to super peers)连接的度概率密度分布呈现“双峰正态分布”特性。Super节点承担Gnutella网络消息路由功能，是整个网络的骨架，节点度频率分布得比较均匀，节点之间的地位比较“平等”，因受客户端软件邻居维护策略的影响。

(2) 拓扑具有小世界特性。同时拥有大聚集系数(Clustering coefficient)和小的平均路径长度(Average path length)2个统计特征的网络，是具有小世界特性的网络。通过Gnutella拓扑的上层节点之间的聚集系数Cactual和平均特征路径长度Lactual，与各次快照拓扑图对应的随机图的聚集系数Crandom和特征路径长度的均值Lrandom进行比较，可以证明Gnutella网络的小世界特性。 Stutzbach等测量了 Gnutella网络数据和 3类典型的具有小世界特性的网络拓扑数据进行比较[15]，结果如表 1所示。Gnutella网络拓扑图满足Cactual＞＞Crandom，且 Lactual≈ Lrandom，即实际网络具有小世界特性。Gnutella网络的聚集系数比文献[14]中的测量结果有所增长，表明Gnutella网络在不断成长时，变得越来越紧密，不利于Gnutella网络中使用洪泛消息路由机制， Gnutella网络比对应的随机网络更容易产生冗余消息。

表1 小世界网络特性Table 1 Property of small-world network

2 虚拟计算环境拓扑建模与构造

iVCE的网络拓扑与当前互联网系统的拓扑具有一定相似之处，但从iVCE的自主元素加入与退出的机制来看，其网络拓扑不可能完全等同于现有复杂网络模型。

2.1 iVCE网络拓扑构造的思想

iVCE从产生到生长到一定的稳定的规模，从而维持一种动态的状态，其网络规模经历了一种迅速扩大，然后进入一种缓慢增加，最后进入一种动态平衡状态的过程。在这个过程中，有些自主元素分化为超级自主元素，同时在超级自主元素的组织管理下形成一些虚拟共同体，即形成社区效应；另外，在自主元素不断加入iVCE时，建立许多新的自主元素间的连接，也有许多自主元素在退出iVCE，或者没有退出iVCE，其连接自主元素在改变。因此，iVCE的网络模型不仅需要能够同时再现小世界效应和无标度特性，而且在具体演化过程中实际的统计性质要符合实际。目前，大部分网络增长模型每一时间步都是加入一个新的节点，网络规模随时间呈线性增长。然而，在现实世界中，网络规模一般随时间的变化是非线性的。在iVCE中，在1个单位时间间隔内，可能有多个新节点同时加入系统，而且随着系统规模的增大，同时加入的新节点数也随之增多，整个系统的规模呈几何级数增长。在网络规模增长的过程中，部分节点会退出网络，最后加入与退出节点达到一种平衡。在此，针对网络演化的实际情况，提出一种包括网络产生、成长、成熟三阶段的网络模型。

2.2 iVCE网络拓扑构造过程

iVCE网络拓扑模型依然采用图G= (V , E ) 来表示。其中：图G是一个无向简单连通图，有N个节点，M条边；V={v1, v2, …, vN}代表节点集合；E={e1, e2, …,eM}⊆V×V，代表边的集合。令 di表示节点 vi的连接度，显然1≤di≤N-1。同时，称D={d , d2, …, dN}为图G的度序列。Dmax-i为节点vi的最大连接度数，由iVCE中自主元素的贡献资源数量和处理能力决定；INTi为vi的兴趣值，区分自主元素的应用类型，从而决定vi的分组、聚集情况。

iVCE网络拓扑生成过程如下。

(1) 网络产生。网络从第1个自主元素开始成长，在网络成长开始阶段，为保持网络的健壮性，当网络规模在阈值Ninit以下时，比如Ninit=20，称其为原始网络，网络中的自主元素不管是超级自主元素还是普通自主元素，相互之间采用全连接，但节点vi的度di不能超过 Dmax-i的限制。为了网络实现过程的更好可行性及健壮性，生成核心网络时，节点的 Dmax-i可设置为相同。此阶段每次只新增加1个自主元素，网络规模呈线性增长。

(2) 网络加速成长。当网络规模大于 Ninit时，网络成长速度加快，每次加入网络多个自主元素，同时网络还有一定的自主元素开始退出网络，加入自主元素数量由当前网络的规模决定。有研究表明，网络成长呈几何级数规模增加，因此，模型中每次增加自主元素数为α×N，退出自主元素数为β×N。其中：β=α×N/Nmax；Nmax为网络预设的最大规模；N为网络当前的规模，当网络规模达到Nmax时，有β=α；α和β分别为加入因子和退出因子，其取值为0～1。

(3) 成熟网络维护。网络规模达到 Nmax后，网络进入一个动态、稳定运行状态，此时，加入网络的自主元素和退出网络的自主元素基本维持平衡。网络规模不是绝对不变的，而是约束在Nmax附近变化，因此，需要在加入、退出的自主元素数中引入随机的扰动量，范围在1～maxN 之间。每次产生2个随机数NRan1和NRan2，假定NRan2＞NRan2，若N＞Nmax，则加入自主元素数为Nα×+NRan2，退出自主元素数为Nβ×+NRan1，反之亦然。

① 自主元素的加入。前面已提及一次加入自主元素的数目，在自主元素生成过程中，以比较小的概率Psuper如5%生成自主元素，使其Dmax-i≥50，该类自主元素作为超级自主元素，以较大的概率(1-Psuper)来生成普通自主元素，使其Dmax-i＜50，为普通的叶子自主元素。对于所生成自主元素的最大连接度 Dmax的分布，采用正态分布比较符合实际；且网络的阈值设为动态可调，以网络的某个整体状态参数作为反馈，来调高或调低阈值。生成自主元素后，则考虑自主元素连接入网，Dmax决定最大连接邻居的数量，NINTi决定了与哪些自主元素相连。

i) 加入叶子自主元素，只选择与NINTi相同的超级自主元素相连，如有多个NINTi，则选择多个超级自主元素连接。因此，提出基于负载压力的连接节点选择策略，选择连接的对象时，主要考虑负载压力，即自主元素当前连接度/自主元素最大连接度的比值Di/Dmax-i，连接时，优先选择Di/Dmax-i小的自主元素连接。因为其具有较小的负载，故具有承担新的任务、连接的能力。

ii) 超级自主元素加入，即加入Dmax-i≥50的自主元素。首先，将其当做叶子自主元素加入网络，可以保证兴趣一致的自主元素组成一个虚拟共同体；然后，再增加一定数量的边比如Dmax×10%连接到其他超级自主元素上。至于连接对象的选择，同样优先连接超级自主元素中负载压力较小的自主元素。

② 自主元素的退出。

i) 普通叶子自主元素退出。将该自主元素从拓扑图中删除，同时删除所有与该自主元素连接的边，并修改连接自主元素的度di。

ii) 超级自主元素退出。将该自主元素从拓扑图G中删除，同时删除所有与该自主元素连接的边，并修改连接自主元素的度di。若与之相连接的叶子自主元素的度为 0，则需要将该自主元素作为一个新的叶子自主元素加入到当前网络中。

该拓扑生成器是iVCE仿真模拟平台的一部分，用 C++语言在linux环境下实现，对数据结构多次优化，具有很好的计算性能和较高存储效率，在 Intel 2.0GHz CPU的主机上，8 min可以生成具有十万数量级规模的拓扑，还可以根据需要展示拓扑生成过程。

3 虚拟计算环境拓扑特性分析

为了分析生成的iVCE网络拓扑的性质，根据上面的方法对网络规模、网络增长因子、自主元素兴趣数以及超级节点的比例等多个参数分别进行调整，在同一组参数条件下重复10次生成网络，对网络的度分布情况、簇系数以及平均最短路径长度分别统计求平均值。

根据需要拓扑生成过程中引入了几个参数。为考察同时加入 iVCE节点的数量，引入增长率α(0＜α＜1)，表示同时加入节点数占当前节点数的比例；超级节点和普通节点连接其他节点的数量不同，引入区别参数超级节点度阈值Dthresh；iVCE中的节点可以基于共同的兴趣而形成相互交互的自治组，因此，引入兴趣数nint。

3.1 iVCE网络拓扑的度分布

在不同网络规模下研究增长率α对所生成网络的度分布的影响。增长率α选取0.01，0.10和0.20，网络规模选取10 000和40 000；兴趣数量为5；以超级节点的最少度数为阈值Dthresh=50，超级节点所占比例为5%。重复进行10次仿真实验，所得到的度分布的平均值如图3所示。从图3可见：增长率α在相当宽的取值范围内(0＜α＜1)，网络的度分布都呈正态分布规律，其峰值约为0.065，出现在节点数为28处。在3(a)中除了最高峰外，在阈值50处还有1个比较明显峰值较低的峰。这主要是因为在拓扑生成的第1个阶段，构造了一个节点度数相同的全连接核心网络。

选取增加因子α=0.1，将兴趣数由原来的5变化为10，阈值由50改为60，在不同网络规模下多次实验，结果如图4所示。从图4可见：不同网络规模下的次级峰明显，网络规模越大，次级峰高度越低。

图3 不同增加因子α下节点度分布Fig.3 Node degree distribution with various increasing factors

从图4可见：多条曲线基本重合，表明网络规模、网络中节点兴趣数对其影响较少，网络规模较少时抖动较严重。进一步，将兴趣数保持为5，增长因子为0.1，将节点超级节点的比例由5%改为10%，在不同网络规模下多次实验，得到网络度分布如图4(c)所示。从图 4(c)可见：节点度分布更加集中，分布中心变为18，峰值达到0.09。由上述实验发现节点度分布主要与超级节点所占比例相关，该比例越低，则度分布正态分布范围更广。

3.2 iVCE网络拓扑的簇系数

不同参数下网络簇系数分布见图5。从图5可见：在α＜1时，簇系数随增长因子的变化不大；当网络的规模从10 000逐步增加到100 000时，簇系数随网络规模增大而减少，变化规律与无标度网络模型一致；当将超级节点的比例由 5%增加为 10%，超级节点的连接度的阈值由50变为60时，超级节点连接度阈值对于簇系数的改变不大；但是，当超级节点比例变为10%时，簇系数明显增加；在网络规模为100 000时，增加比例达50%。

图4 不同兴趣数、阈值和超级节点比例下节点度分布Fig.4 Node degree distribution with various interests and thresholds

3.3 iVCE网络拓扑的平均最短距离

图5 不同参数下网络簇系数分布Fig.5 Cluster coefficient distribution with various parameters

平均最短距离是复杂网络的一个重要统计特性，小的平均最短距离意味着网络具有小世界特性。对不同增长率下生成网络的平均最短距离进行计算，结果如图6所示。从图6可看出：随着网络规模从10 000递增到100 000，网络平均最短路径长度L从5.3增加到6.8。

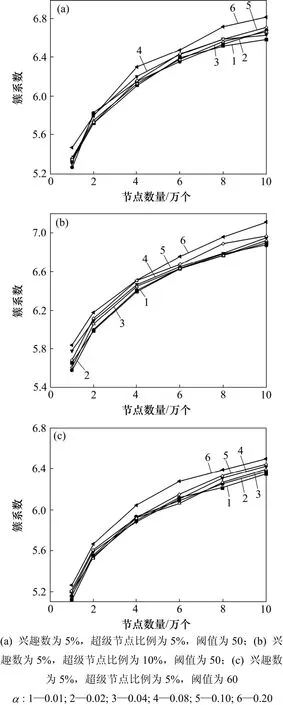
图6 不同参数条件下网络平均最短路径长度Fig.6 Average shortest path length with various parameters

同时发现：网络增长因子对L影响不大，增长因子大的网络，其L也略大。将超级节点的比例由5%增加为 10%，相应地将超级节点连接度的阈值由 50变为60，发现当超级节点比例增加为10%时，平均最短路径长度增加 0.2；当超级节点连接度阈值增加为60时，平均最短路径长度在网络规模比较小时基本保持不变，但当网络规模不断增大时，长度明显降低；当节点数达到 100 000时，平均最短路径长度由 7.1减少为6.5。

从网络的生成过程和网络属性的统计分析情况来看，网络的度分布、簇系数、平均最短距离比较稳定，参数值的改变对其分布影响较少。影响网络属性变化的重要因素是网络节点动态加入和退出过程的连接方案以及拓扑维护的策略，iVCE网络采用基于负载压力的连接节点选取，使得网络节点度分布呈现正态分布，因此，能够较好地实现负载的均衡分配，同时，网络的稳定性和可靠性均比较好，一批处理能力强的超级节点具有较高的连接度，从而保证了网络整体的生存性比较好。从网络的效率方面来看，网络具有幂率分布基本一致的平均最短路径长度，具有小世界网络的特征，从而保证消息传输的开销较少。

4 结论

(1) 在对Gnutella为代表的P2P系统的拓扑进行分析的基础上，基于复杂网络模型，提出了一种包括产生、成长和成熟运行三阶段同时多节点快速增长的网络拓扑生成方法。

(2) 该方法通过控制网络增长因子、超级节点比例、兴趣数以及超级节点阈值，生成具有一定值的节点度分布频率、聚集系数、平均节点间最短路径长度属性指标的网络拓扑。分析形成的网络拓扑发现生成的iVCE拓扑具有很强的稳定性。

(3) 采用基于负载压力的节点连接选择策略使得整个网络具有良好的负载均衡的效果，能基于超级节点能力分配合适的连接节点，而不会出现超大连接度节点，提高了系统的可靠性。

[1] 卢锡城, 王怀民, 王戟. 虚拟计算环境 iVCE: 概念与体系结构[J]. 中国科学 E辑: 信息科学, 2006, 36(10): 1081-1099.LU Xi-cheng, WANG Huai-min, WANG Ji. Internet-based virtual computing environment[J]. Science in China Ser E.Information Sciences , 2006 , 36 (10): 1081-1099

[2] Faloutsos C, Faloutsos M, Faloutsos P. On power-law relationships of the Internet topology[C]//Proc of the ACM SIGCOMM. New York, 1999: 251-262.

[3] Albert R, Jeong H, Barabasi A L. Error and attack tolerance in complex networks[J]. Nature, 2000, 406: 387-482.

[4] Newman M. Properties of highly clustered networks[J]. Physical Review E, 2003, 68: 026121.

[5] Erdös P, Rényi A. On the evolution of Random graphs[M].Hungary: Publication of the Mathematical Institute of the Hungarian Academy of Sciences, 1959: 290-297.

[6] Calvert K L, Doar M. Modeling Internet topology[J]. IEEE Communications Magazine, 1997, 35(6): 160-163.

[7] Winick J, Jamin S. Inet-3.0: Internet topology generator[R].Technical Report, CSE-TR-456-02, Department of EECS.University of Michigan, Michigan, USA, 2002.

[8] Albert R, Barabari A L. Topology of evolving networks: local events and university[J]. Physical Review Letters, 2000, 85(24):5234-5237.

[9] Jovanovic M A. Modeling large-scale peer-to-peer networks and a case study of Gnutella[D]. Ohio: University of Cincinnati,2001: 102-113.

[10] Stutzbach D, Rejaie R, Sen S. Characterizing unstructured overlay topologies in modern P2P file-sharing systems[J].IEEE-ACM Transactions on Networking, 2008, 16(2): 267-280.

[11] 刘刚. 对等网络的测量、模型化与分析[D]. 哈尔滨: 哈尔滨工业大学计算机学院, 2005: 80-89.LIU Gang. Measurements, modeling and analysis of peer-to-peer networks[D]. Harbin: Harbin Institute of Technology. School of Computer, 2005: 80-89.

[12] 王勇, 云晓春, 李奕飞. 对等网络拓扑测量与特征分析[J]. 软件学报, 2008, 19(4): 981-992.WANG Yong, YUN Xiao-chun, LI Yi-fei. Measuring and characterizing topologies of P2P networks[J]. Journal of Software, 2008, 19(4): 981-992.

[13] Nowak M A. Five rules for the evolution of cooperation[J].Science, 2006, 314: 1560-1563.

[14] Pouwelse J P, Garbacki P, et al. The Bittorrent P2P file-sharing system: Measurements and analysis[C]//Castro M, van Renesse R, ed. Peer-to-Peer Systems IV, IPTPS 2005. Ithaca:Springer-Verlag, 2005: 205-216.

[15] Watts D J. Networks, dynamics and the small world phenomenon[J]. American Journal of Sociology, 1999, 105(2):493-527.

[16] Albert R, Barabási A. A statistical mechanics of complex networks[J]. Reviews of Modern Physics, 2002, 74(1): 47-97.