基于目标机动检测的集成估计与制导方法

花文华，陈兴林，宋申民

(哈尔滨工业大学 航天学院，黑龙江 哈尔滨，150001)

传统的估计器和制导律独立优化设计方法在实际的目标拦截情形中其综合性能不是最优的。集成估计与制导设计方法首先由Shinar等[1]提出，但对于目标机动切换时间的辨识没有给出明确的方法。Shaviv等[2]尝试在一个具有一般性的非线性非Gaussian框架内将估计器和制导律的设计相结合，在对传统的可达集概念扩展的基础上，在制导律的设计中考虑估计量的条件概率密度函数。然而，该方法计算量较大且仍然需要验证。唐治理等[3]对于集成估计/制导/控制系统的综合设计方法进行了研究，但并没有给出具体的方案。Shinar等[4]给出了一种基于逻辑的集成估计与制导算法，采用高效多模型自适应估计器[5]，对一类具有随机时间转换的目标机动进行辨识，并采用待飞时间对制导律进行修正，以减小估计误差；在此基础上，又从三维的角度，考虑实际的大气层内弹道导弹拦截情景中导弹与目标的速度和机动能力的时变性，对该设计方案的可行性进行了验证[6]。在此，本文作者基于目标机动检测对集成估计与制导设计方法进行了进一步研究，给出一种适用于随机机动目标拦截的自适应集成估计与制导方法。该方法由目标机动命令切换的检测时间对估计器和制导律对进行在线选择，从而削弱目标机动估计延迟的影响，改善导弹寻的性能。其步骤是：首先对所要研究的主要问题进行描述和建模，给出弹目运动关系的数学描述以及量测和性能指标；然后，对微分对策制导律(Differential game guidance law，DGL)和指数相关加速度(Exponentially correlated acceleration，ECA)成型滤波器(Shaping filter，SF)的性能进行分析；在此基础上，给出基于目标机动检测的自适应集成估计与制导方法，最后进行仿真和性能分析。

1 问题描述及建模

1.1 弹目运动关系数学描述

制导末端的弹目运动关系如图1所示。X轴沿初始视线方向，下标P和E分别对应拦截导弹和目标的相关状态，y表示弹目相对于初始视线方向的位移。基于下述假设对问题进行分析：

(1) 拦截导弹和目标可近似为具有线性动态特性的质点，并可沿初始视线方向进行线性化；

(3) 拦截导弹和目标近似具有一阶机动动态；

(4) 拦截导弹可对相对运动关系和自身的相关状态在噪声下进行量测，目标无法获取拦截导弹的相关信息，但可意识到拦截企图，从而随机规避机动。

图1 平面弹目运动关系Fig.1 Planar engagement geometry

wE和 wP是相互独立的零均值高斯白噪声；标准方差分别为σE和σP；τP和τE分别为拦截导弹和目标的机动时间常数。

基于假设(1)和(2)，拦截导弹飞行时间为：

其中：r0为弹目初始距离；vc为接近速度，近似为vP+vE。待飞时间tgo可表示为：

对系统(1)进行离散化，可以得到：

其中：

T为采样周期。

1.2 量测

结合图 1，采用一定的弹上量测设备对弹目距离r、视线角q和拦截导弹横向加速度aP进行量测。假设r是可精确量测的，q和aP具有一定的量测噪声，并假设噪声为白噪声且符合高斯分布，标准方差分别为σq和σaP，则量测方程可表示为：

1.3 性能指标

在真实环境中，拦截导弹在应对机动目标拦截时，其杀伤性能一般很难予以描述，它除了依赖于精确的弹目运动关系外，还取决于许多其他物理参数。对于基于质点运动假设的对象，在无其他终端约束时，脱靶量是唯一可用于评估拦截导弹杀伤性能的参数。本文主要采用一个脱靶量阈值函数以确定目标的拦截概率：

其中：∆为阈值，近似为拦截导弹杀伤半径。由于量测噪声和目标机动的随机性，脱靶量是1个未知分布的随机变量。大量的Monte Carlo实验可以实现脱靶量累积概率分布函数的经验估计，从而进行不同制导律之间的性能比较，因此，单发杀伤概率(PSSK)可以作为目标有效拦截所需概率的量测标准。PSSK为 Ps(∆)的数学期望，可表示为：

PSSK考虑了量测噪声和随机目标机动的影响。拦截导弹要求PSSK最大化，而目标则要求PSSK最小化。

2 DGL和ECA SF寻的性能分析

2.1 范数型DGL性能分析

近年来微分对策理论在目标拦截[7-8]、飞行器姿态控制[9]、威胁规避[10-11]、火力分配[12-13]等方面的应用得到深入研究。在目标拦截方面，由于目标是独立控制的，其机动策略一般是无法预测的，将机动目标拦截定义为最优控制问题并不合适[14]；而对于零和微分对策问题，双方都是独立控制的，一方要求性能指标最大化，而另一方要求性能指标最小化。且与基于最优控制理论的制导律相比，微分对策制导律对于目标机动估计误差具有更强的鲁棒性[15]。

范数型微分对策制导律[16]是指具有有界控制和采用零效脱靶量性能指标的零和微分对策拦截情形。基于对策最优的必要条件和对目标机动动态的不同假设，在一阶或理想特性下，相应的微分对策制导律表示为：

其中：z1(t)和 z0(t)为零效脱靶量，对应于拦截导弹和目标由给定的时间t不施加任何控制，以该瞬时参数飞行至命中，所产生的脱靶量为：

文献[17]给出了一种估计延迟部分补偿的微分对策制导律。将目标加速度由估计延迟所产生的加速度集的中心值代替，则

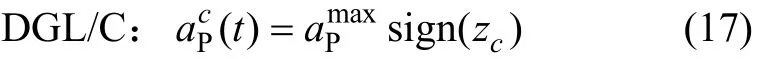
其中：

Δtest为目标加速度估计延迟。

DGL/1和DGL/C的执行需要相关信息完全已知(Perfect information)情况下的零效脱靶量z1(t)和zc(t)，包括目标的横向加速度aE。这一变量一般无法直接量测，只能通过估计器进行观测。而对于具有随机时间切换的目标机动，估计延迟将不可避免[18]。

图2所示为采用微分对策制导律DGL/0，DGL/1和 DGL/C对具有一次时间切换的“bang-bang”机动目标拦截的性能比较。目标机动命令切换时间tsw在整个飞行段内均匀分布，应用ECA SF表示目标的机动策略，仿真参数如表 1所示。具有随机时间切换的“bang-bang”机动被认为是最优的目标规避机动[4,6]。从图 2可以看出：当滤波器具有足够的收敛时间时，DGL/1具有最好的目标拦截性能，但在tsw=2.3 s附近，脱靶量则较大；DGL/0对于较早的目标机动命令切换，脱靶量比 DGL/1的大，但由于未考虑目标机动的影响，在tsw=2.3 s附近的脱靶量则明显比DGL/1的低；DGL/C的性能介于DGL/0和DGL/1之间的性能，当采用较大的延迟补偿时，DGL/C的性能与DGL/0的接近；当目标加速度估计延迟 Δtest→0时，其性能与DGL/1的接近。

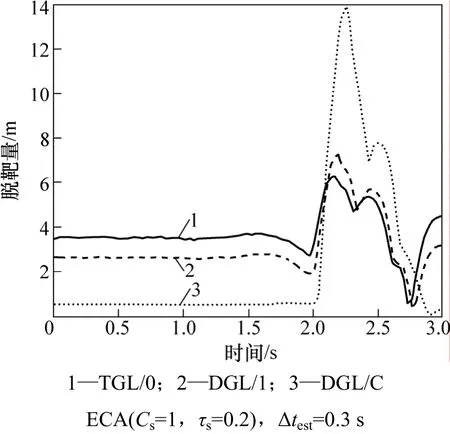
图2 DGL拦截性能比较Fig.2 Performance comparison against target interception of DGL

表1 仿真参数Table 1 Simulation parameters

2.2 ECA SF性能分析

ECA SF即singer 目标机动模型，具有2个可调参数：目标的机动时间常数τs和噪声水平参数Cs。对于给定的量测噪声，这2个参数影响到估计器的带宽，进而影响估计器的收敛时间和目标机动命令发生切换时的估计延迟以及估计误差方差。

图3所示为采用1 000次Monte Carlo试验和制导律DGL/1对具有不同带宽的ECA SF进行“bang-bang”机动目标拦截的性能比较。其中：Cs=1；τs=0.2，0.5，1.0和1.5。4个滤波器且取相同的目标机动命令切换时间和噪声随机数产生器种子。从图3可以看出：当估计器具有较高的带宽，且 PSSK=0.95时具有较小的脱靶量，而当PSSK＜0.75时，较低带宽的估计器具有较好的性能。这主要是由于较高的带宽可以减少估计器的响应时间，从而在估计器无足够的收敛时间时，如图2中tsw=2.3 s附近，与低带宽估计器相比，仍能够获得较好的寻的性能；而低带宽估计器由于具有较高的估计精度，当具有足够的收敛时间时，可以提供较好的寻找性能。

图3 不同带宽ECA SF进行目标拦截的性能比较Fig.3 Performance comparison of different bandwidths ECA SF against target interception

3 集成估计/制导方法

由上述分析可以发现：采用相应的制导律和成型滤波器的拦截导弹寻的性能受到目标机动估计延迟的影响，且不同制导律和不同带宽的滤波器具有不同的情况。基于这一点，给出一种自适应集成估计/制导方法。

3.1 广义似然比检测简述

基于广义似然比(Generalized likelihood rate, GLR)检测方法，对事先假定的目标机动命令所对应的似然比进行检测，从而识别目标机动命令的相关特性，包括切换幅值和切换时间。构建假设集 H={Hi，i=0，1，…，N}用于描述目标机动命令序列的所有可能的相关实现方法，H可随时间更新，其中H0表示切换未发生的假设情况，Hi(i=1，…，N)表示具有不同目标机动切换时间和切换幅值 fi的情形。GLR检测首先将假设集转换为通过在线估计获得的量测分布，并基于这些分布和似然比2次的最大化以决定切换的发生及其特征：

其中：L(Hi，H0)为似然比；G为决策函数。切换是否发生即可通过G与1个设定的阈值h进行比较得到判断；h由一自由度中心卡方(Central chi-square)分布确定。

基于离散化系统方程(4)，假设 γ(k)，S(k)和 K(k)分别为相应于H0的参考Kalman滤波器的新息，新息协方差和滤波增益矩阵，则

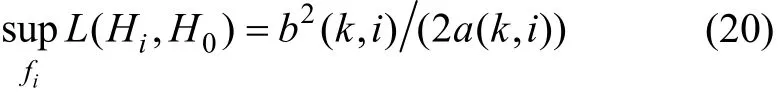
其中：

3.2 集成估计/制导方法

该集成估计/制导方法主要由滤波器组、制导律组和1个目标机动命令切换时间检测器构成。首先采用GLR检测方法对目标机动命令切换进行检测，且一旦得到检测，即可由检测时间swˆt进行滤波器和制导律对的在线选择，如图4所示。图4中：ε为一个二元指示器，ε=1表示目标机动切换已经得到检测，且检测时间为swˆt。

通过对 DGL的性能分析可知：目标机动估计延迟对DGL/1的性能影响最明显，但当估计器具有足够的收敛时间时，其也具有最好的寻的性能；DGL/0由于假设目标具有理想机动动态，估计延迟对其并无明显影响；这2种制导律形成了一种互补关系，因此，选择二者构成制导律组。滤波器组由包含不同带宽的ECA SF和Kalman滤波器组成，高带宽滤波器可以保证估计器的快速响应，从而削弱估计延迟的影响；低带宽滤波器具有较高的滤波精度，从而保证拦截导弹的寻的性能。

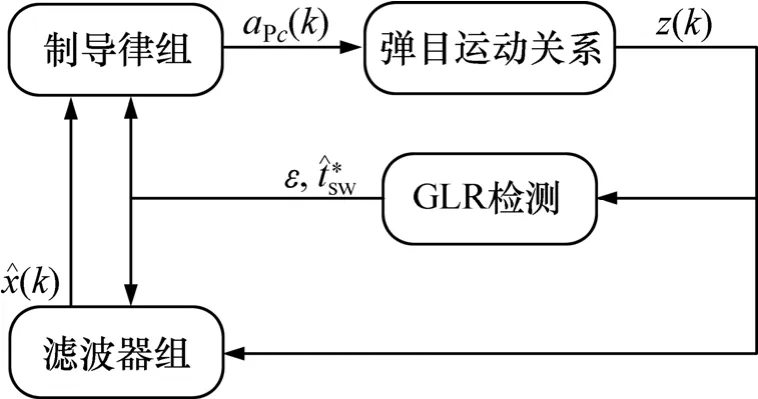
图4 自适应集成估计/制导方法Fig.4 An adaptive approach of integrated estimation/guidance

以2个滤波器E0和E1为例，其中，E0和E1分别对应包含较高带宽和较低带宽的 ECA SF的 Kalman滤波器。整个自适应集成估计/制导过程可描述为：

其中：tc为集成估计/制导临界切换时间，可通过大量的离线Monte Carlo仿真实验确定的与飞行时间经计算得到。起始阶段目标机动切换未检测，选择(E1，DGL/1)对，若swˆt＜tc，则估计器具有足够的收敛时间，保持(E1，DGL/1)对不变；当swˆt ≥tc时，要求估计器具有较快的响应，以削弱估计延迟的影响，选择(E0，DGL/0)对。该集成估计/制导方法表示为DGL/I。

4 仿真结果及分析

主要针对一类迎面末端拦截情形进行仿真研究，如图 1所示。假设目标机动为具有一次时间切换的“bang-bang”类型，γP(0)≈0，γE(0)≈0，tc=2.3 s，仿真中选取2个具有不同带宽的ECA SF，为E0:{Cs=1，τs=1.5}和E1:{Cs=1，τs=0.2}，其他仿真参数如表1所示。

图5所示为采用GLR方法对目标机动命令切换时间进行检测的误差曲线，h=13 (虚警概率近似为0.000 2)，制导律为DGL/1。从图5可以看出：检测器可对tsw∈[0.5，2.9]范围内的目标机动命令切换进行检测，但无法完成起始阶段和末端的切换检测。起始阶段在估计器收敛时间受到约束和缺少足够检测目标机动命令切换的信息下进行检测，而末端则是在缺少足够的时间时对目标机动命令切换进行检测。虽然出现了无法检测的机动命令切换时间段，但并不会影响所设计的集成估计/制导方法的寻的性能。假设切换发生在起始阶段，此时估计器具有足够的收敛时间，应选择(E1，DGL/1)对以改善寻的性能；对于末端，只需要选取 tc≤2.9 s，采用(E0，DGL/0)对可以削弱估计延迟的影响。这与所设计的自适应集成估计/制导方法一致。

图6所示为目标机动命令切换时间tsw=2.3 s时，采用DGL/1的脱靶量变化曲线。从图6可以看出：在目标机动命令切换得到检测之前，采用(E1，DGL/1)估计/制导对，由于延迟的影响，swˆt ＞tc，从而在t=2.3 s时切换到(E0，DGL/0)对。这一过程也可从图7所示的拦截导弹加速度变化曲线得到反映。

图5 目标机动命令切换时间tsw检测误差Fig.5 Detection errors of target maneuver command timed switch tsw

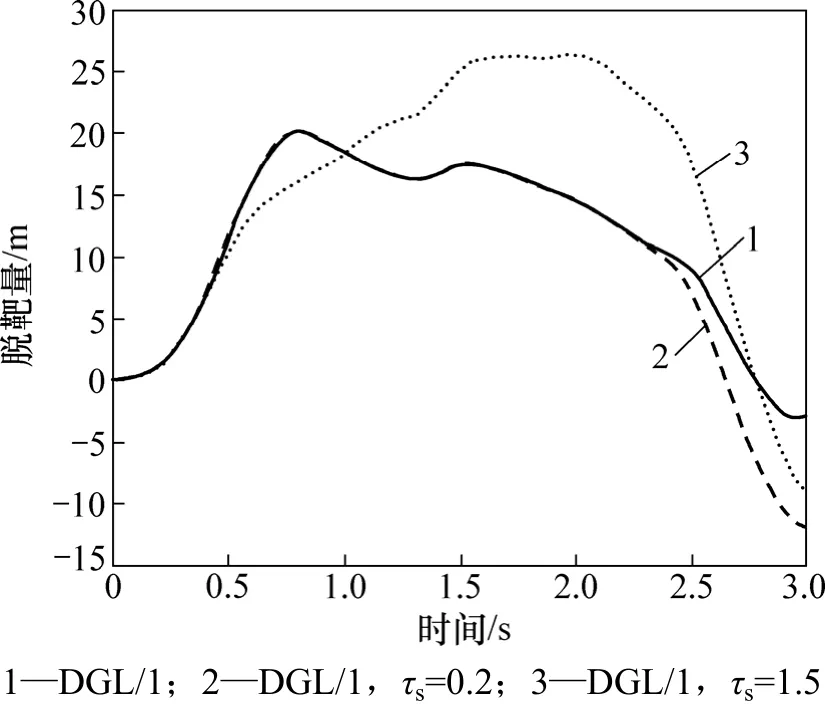
图6 tsw=2.3 s时脱靶量变化曲线Fig.6 Miss distance when tsw=2.3 s

图7 拦截导弹加速度tsw=2.3 sFig.7 Missile accelerations when tsw=2.3 s

图8 所示为基于1 000次Monte Carlo试验的目标拦截性能比较曲线。从图8可以看出：本文给出的自适应集成估计/制导方法具有最好的目标拦截性能；对于给定的 PSSK，例如 PSSK=0.95，采用 DGL/I所要求的弹头杀伤半径比DGL/1的小。

图8 目标拦截性能比较Fig.8 Performance comparison against target interception

5 结论

(1) 给出了一种可适用于随机机动目标拦截的自适应集成估计与制导设计方法。该方法由目标状态的估计和机动命令检测特征，采用最有效的估计器与制导律，削弱了目标机动估计延迟对导弹命中概率的影响。

(2) 基于Monte Carlo试验法进行仿真，该设计方法与具有单一滤波器和制导律的方法相比，对于一个给定的脱靶量具有较高的单发命中概率。这一设计思想的关键要素是目标机动命令的切换检测，因此，对快速突变检测器的研究成为后续研究的重点。

[1] Shinar J, Oshman Y, Turetsky V. On the need for integrated estimation/guidance design for hit-to-kill accuracy[C]//Proceedings of the American Control Conference. Denver,Colorado, 2003: 402-407.

[2] Shaviv I G, Oshman Y. Fusion of estimation and guidance using sequential monte carlo methods[C]//Proceedings of IEEE Conference on Control Applications, Institute of Electrical and Electronics Engineering, New York, 2005: 1361-1366.

[3] 唐治理, 雷虎民, 邵雷, 等. 拦截器多模估计/制导/控制系统综合设计方法[J]. 航天控制, 2009, 27(3): 76-85.TANG Zhi-li, LEI Hu-min, SHAO Lei, et al. Multi-model estimate/guidance/control system integrated design for interceptor[J]. Aerospace Control, 2009, 27(3): 76-85.

[4] Shinar J, Turetsky V, Oshman Y. Integrated estimation/guidance design approach for improved homing against randomly maneuvering targets[J]. Journal of Guidance, Control and Dynamics, 2007, 30(1): 154-161.

[5] Shima T, Oshman Y, Shinar J. An efficient application of multiple model adaptive estimation in ballistic missile interception scenarios[J]. Journal of Guidance, Control and Dynamics, 2002, 25(4): 667-675.

[6] Shinar J, Turetsky V. Three-dimensional validation of an integrated estimation/guidance algorithm against randomly maneuvering target[J]. Journal of Guidance, Control and Dynamics, 2009, 32(3): 1034-1038.

[7] 马礼举, 魏志鹏. 基于目标姿态信息的导弹微分对策制导律研究[J]. 弹箭与制导学报, 2009, 29(3): 43-46.MA Li-ju, WEI Zhi-peng. The design of differential game guidance law based on target attitude[J]. Journal of Projectiles,Rockets, Missiles and Guidance, 2009, 29(3): 43-46.

[8] 左斌, 扬长波, 李静. 基于微分对策的导弹攻击策略[J]. 海军航空工程学院学报, 2005, 20(5): 524-526.ZUO bin, YANG Chang-bo, LI Jing. Missiles attack games based on differential games[J]. Journal of Naval Aeronautical,2005, 20(5): 524-526.

[9] 苏晓丹. 飞行器姿态控制系统综合的一种微分对策方法[J].航天控制, 2009, 27(3): 72-75.SU Xiao-dan. Differential game method of attitude control system synthesis for flight vehicle[J]. Aerospace Control, 2009,27(3): 72-75.

[10] 王长青, 史晓丽, 王新民, 等. 基于 LQ微分对策的最优规避策略与决策算法[J]. 计算机仿真, 2008, 25(9): 74-78.WANG Chang-qing, SHI Xiao-li, WANG Xin-min, et al.Optimal evasive strategies based on LQ differential games[J].Computer Simulation, 2008, 25(9): 74-78.

[11] 胡云安, 张新立, 李晓东, 等. 基于微分对策的导弹最优突防策略[J]. 海军航空工程学院学报, 2007, 22(1): 169-172.HU Yun-an, ZHANG Xin-li, LI Xiao-dong, et al. Missile optimal penetration method based on differential games[J].Journal of Naval Aeronautical Engineering Institute, 2007, 22(1):169-172.

[12] 李登峰, 罗飞. 舰艇编队信息战火力分配微分对策模型及求解[J]. 控制理论与应用, 2008, 25(6): 1163-1166.LI Deng-feng, LUO Fei. Differential game model and its solution for the firepower-assignment in vessel formations in information war[J]. Control Theory & Applications, 2008, 25(6):1163-1166.

[13] 罗飞, 李登峰, 陈庆华. 舰艇编队导弹攻击火力分配微分对策模型[J]. 装备指挥技术学院学报, 2003, 14(5): 89-92.LUO Fei, LI Deng-feng, CHEN Qing-hua. Differential games model of warships missile allocation[J]. Journal of Journal of Institute of Command and Technology, 2003, 14(5): 89-92.

[14] Anderson G M. Comparison of optimal control and differential game intercept guidance laws[J]. Journal of Guidance and Control, 1981, 4: 109-115.

[15] Zarchan P. Tactical and strategic missile guidance[M].Washington DC: AIAA, 1990: 87-110, 155-175.

[16] Turetsky V, Shinar J. Missile guidance laws based on pursuit-evasion game formulations[J]. Automatica, 2003, 39(4):607-618.

[17] Shinar J, Shima T. Nonorthodox guidance law development approach for intercepting maneuvering targets[J]. Journal of Guidance, Control and Dynamics, 2002, 25(4): 658-666.

[18] Glizer V Y, Shinar J. Optimal evasion from a pursuer with delayed information[J]. Journal of Optimization Theory and Applications, 2001, 111(1): 7-38.