金属间化合物的标准生成焓估算模型

赵定国，郭培民，赵沛

(钢铁研究总院 先进钢铁流程及材料国家重点实验室，北京 100081)

化合物生成焓的测定是冶金和材料领域长期需要开展的基础研究。测定化合物的热力学标准生成焓的方法很多，同一种化合物的实验结果也常常有差异，且实验方法的可靠程度也有待研究[1]。现有的无机化合物中，大部分物相的物性是未知的或不确定的，各种热力学数据手册及电子数据库也仅针对已知数据，更多的热力学数据却不能得到，因此，通过理论分析和实验规律建立的物性估算方法是非常重要的。人们希望能从理论上来计算标准生成焓，这就需要建立必要的模型。20世纪70年代中期，米德玛(Miedema)和其合作者通过联合热力学概念和电子结构理论建立了化合物标准生成焓估算模型[2]，取得了较好的成果，但对于很多金属间化合物的估算仍存在较大误差[3]，如部分镧系物相误差达到90 kJ/mol，且对于多原子化合物误差更大；Ray等[4]建立了扩展的米德玛模型，考虑了弹性能和结构能，应用于估算Zr-Cu-Ni等三元合金体系；拉蒂默的离子束缚模型也是一种很有代表性的估算模型[5]，但是它对于很多金属间化合物的计算精度也不高，且无法计算Al系金属间化合物的有关参数，属于半理论半经验模型；国内一些学者对一些简单的金属间化合物进行了实验研究和计算[6]，但仍然局限于前人的模型，计算的化合物仅针对某一体系，种类有限。金属间化合物均是由不同原子以不同的个数组合出来的，每种原子均有本征热力学属性(如标准熵等)，同时金属之间还存在相互作用的热力学属性；而本征热力学属性、相互作用热力学属性、原子个数和化合物热力学相应属性之间是存在一定关系的，通过对大量的化合物的统计计算，郭培民等[7-9]提出了双参数估算模型，已用于估算复合氧化物的标准熵、标准生成焓与比热容，双参数模型还能很好地估算金属间化合物的标准熵和比热容[10-11]。为了解决目前金属间化合物的标准生成焓的估算方法不准确问题，本文作者将利用双参数模型对金属间化合物的标准生成焓进行研究。

1 模型建立

对于金属间化合物MxNy，M和N为组成该化合物的金属的符号，x和y分别为它们的系数。假定MxNy的标准生成焓由2个部分组成：一部分为单质金属的贡献焓；另一部分为单质金属间的相互作用焓。其表达式为：

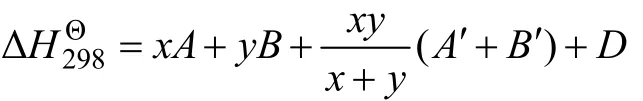
由于每种单质金属均含有2个参数，因此，将此模型称为“标准生成焓的双参数模型”。模型中的参数需要利用已知二元金属间化合物的标准生成焓通过回归方法求得。

双参数模型中参数的求解需要利用已知二元金属间化合物的标准生成焓，因此，二元金属间化合物标准生成焓的数据是否全面、准确和充分，直接关系到模型的可靠程度。在多种无机物热力学数据手册中查得109个二元金属间化合物的标准生成焓[12-15]，涉及Fe，Si，Ca，Al和U等34种金属，相当于每个金属有 6.4个数据，因此，从统计学角度来看，本文的回归统计也更具有可靠性。在这些二元金属间化合物中，钙化物占10个，铁化物占8个，硅化物占51个，铝化物占10个，铀化物占25个，镍化物占10个，钛化物占9个等。

在回归统计中，需要计算平均标准差S和相关系数 R，用以考察模型的可靠性和估算误差。S越小，表明估算误差越小；R越接近 1，表明模型的可信度越高。S和R的计算式分别为：

式中：yi和 yˆi分别为某个二元金属间化合物的实测标准生成焓和估算标准生成焓；y为所有二元金属间化合物的标准生成焓平均值。

2 计算结果

通过数据分析和模型求解，能够得到34种金属的A，A′和常数 D(-1.119 kJ/mol，298 K)，结果见表 1；估算了金属间化合物的标准生成焓，部分数据见表2。利用双参数模型，估算的平均误差为12.47 kJ/mol，相关系数为0.992。从统计学角度来看，双参数模型是可靠的。109个数据的标准差S为17.40 kJ/mol，其中误差大于3S(52.20 kJ/mol)的数据只有1个，占总数据的0.92%；大于2S(34.80 kJ/mol)的数据有6个，占总数据的5.51%；大于1S(17.40 kJ/mol)的有31个，占总数据的28.44%。图1所示为标准生成焓误差的分布。从图1可见：双参数模型109组数据的标准生成焓误差符合正态分布。

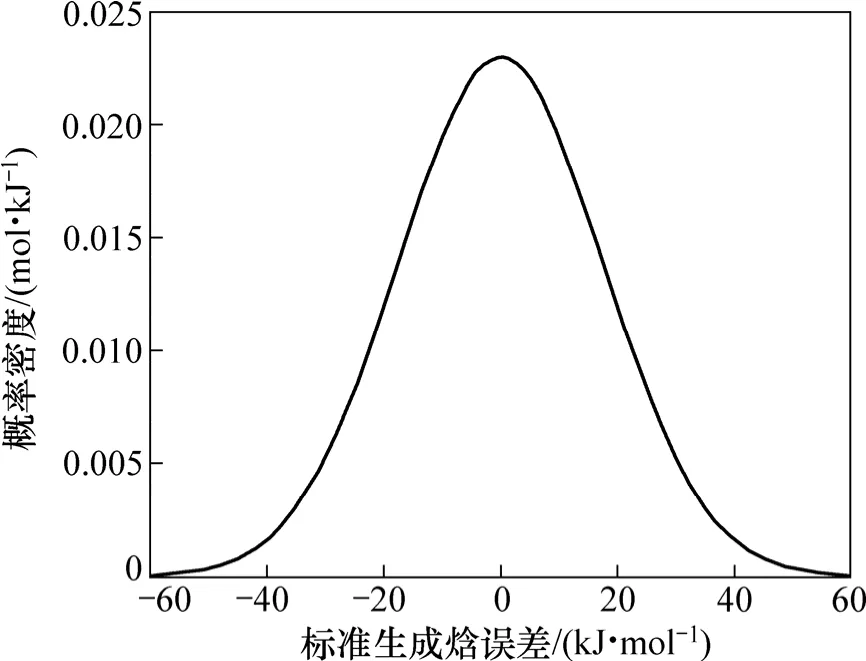
图1 标准生成焓误差的分布Fig.1 Error distribution of standard enthalpy

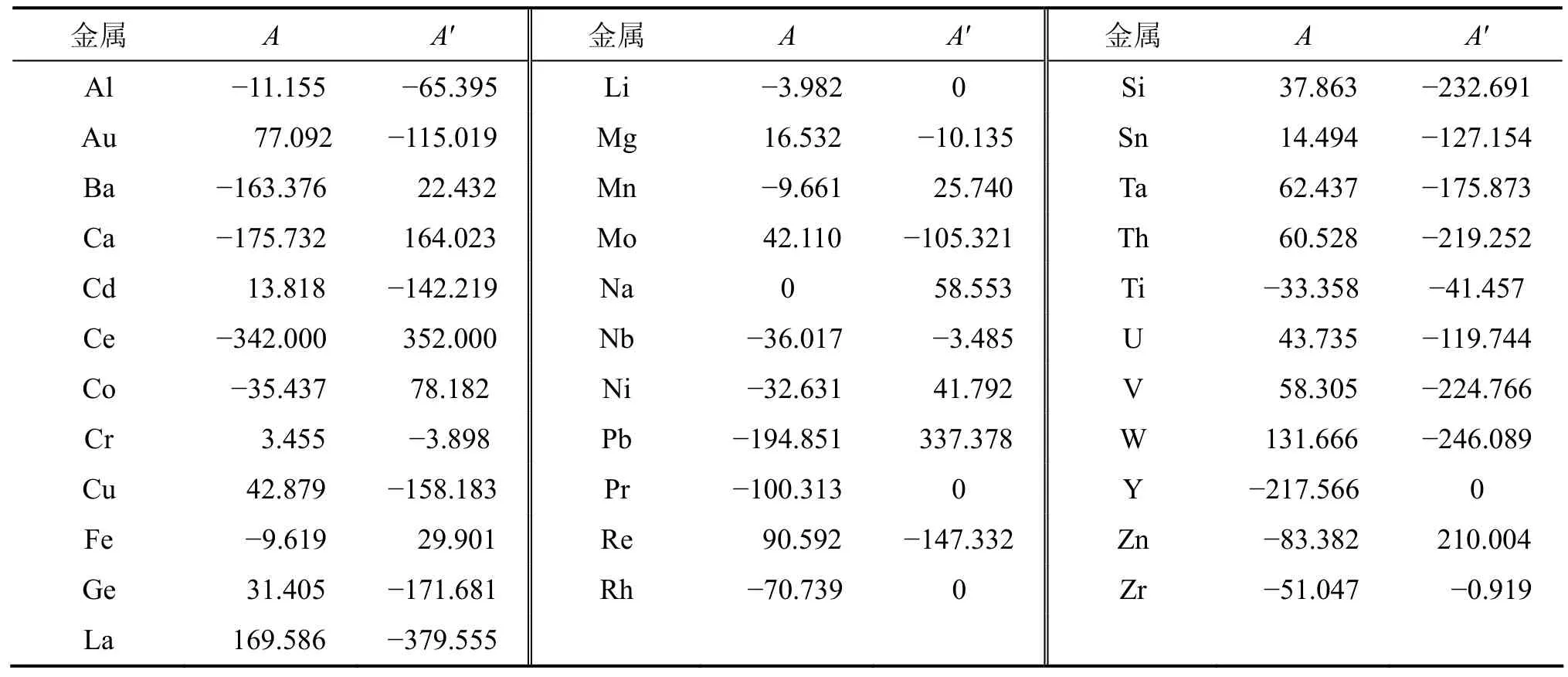
表1 金属的A和A′Table 1 A and A′ of metal kJ/mol

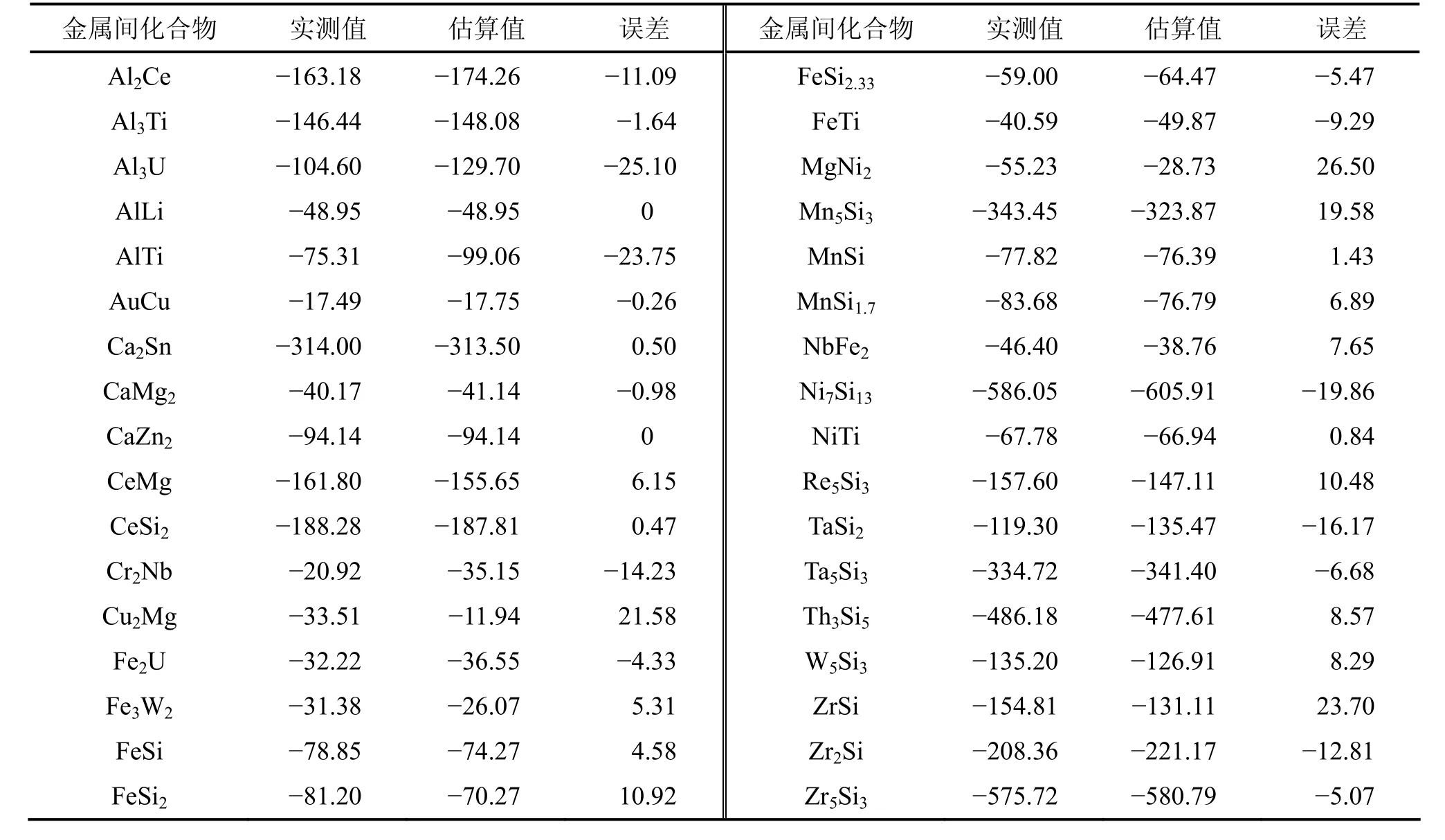
表2 部分金属间化合物的标准生成焓Table 2 Part of standard enthalpies of intermetallics kJ/mol

3 各种模型的比较

建立金属间化合物的估算模型，是用来预测未知物相的标准生成焓，如果模型本身估算的数据与已测实验数据相差很大，那么用模型估算未知物相的可靠性就很低。金属间化合物数据众多，其中硅系化合物个数最多，其热力学数据经过前人的实验测得，以它作为比较对象具有代表性。

米德玛及其合作者建立了米德玛模型用以估算金属间化合物的标准生成焓：

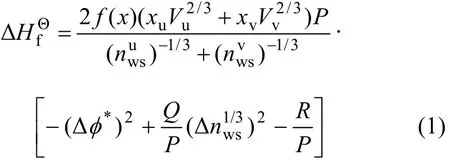
Miedema等[16-17]考虑的合金化效应及他们用来描述这种效应所使用的2个半经验参数nws和φ*均属于电子因素[16-17]，式(1)描述了形成固态或液态合金的2种原子参数的能量影响，第1项是由2种原子的晶粒化学势之差引起的；第2项为在2种不同原子晶粒边界和威格纳-赛茨(Wigner-Seitz)纯晶粒边界形成连续电子密度所需能量；最后1项是修正项。P和R均是用经验的方法调整得到的常数。米德玛模型能估算至少某一组分为过渡金属元素形成二元合金的反应热。

对于金属间化合物应用离子束缚模型，可以推导出二元金属间化合物MxNy的标准生成焓为：

式中：xi为化合物中组元i的浓度；Ei和Ci为根据实验数据和估算模型用最小二乘法确定的参数。

这里必须指出，离子束缚模型不适用于含铝的金属间化合物，否则将产生很大的偏差。

将米德玛模型和离子束缚模型与双参数模型估算的硅系化合物标准生成焓误差进行了比较，数据见表3。令金属间化合物的实测值与估算值之差的绝对值为绝对误差(正数)，用 dj表示；绝对误差与实测绝对值之比的百分数为相对误差，用dx表示。即

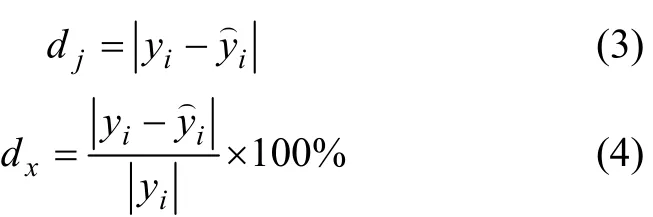
图2所示为3种模型的绝对误差比较。从图2可看出：米德玛模型估算的标准生成焓的绝对误差较大，双参数模型标准生成焓的绝对误差dj大多比离子束缚模型的要小，51种化合物中，有33种金属间化合物的误差比离子束缚模型的小。并且离子束缚模型有 6组数据绝对误差大于50 kJ/mol，最大达109.54 kJ/mol，而双参数模型最大误差也只有46.40 kJ/mol，且波动较小。图3所示为3种模型的相对误差比较。从图3可看出：双参数模型的相对误差dx比离子束缚模型的也要小，误差较大的也很少。

双参数模型估算金属间化合物标准生成焓的标准差为17.17 kJ/mol，而离子束缚模型为31.96 kJ/mol，米德玛模型为67.09 kJ/mol，双参数模型要比离子束缚模型和米德玛模型的标准差要小很多，指标比离子束缚模型和米德玛模型的优。图4所示是2种模型偏差的正态分布。由图4可见：双参数模型偏差的正态分布呈尖峰形，说明偏差比较集中，都在0附近；而米德玛模型和离子束缚模型的偏差正态分布呈秃峰形，说明偏差较大且分散，其中米德玛模型的分散程度最大。因此，金属间化合物标准生成焓的双参数模型对数据的估算比离子束缚模型和米德玛模型有更高的准确度。

表3 硅系金属间化合物估算误差比较Table 3 Estimating error comparison of intermetallics containing silicon kJ/mol

图2 3种模型的绝对误差比较Fig.2 Comparisons of absolute error of three models

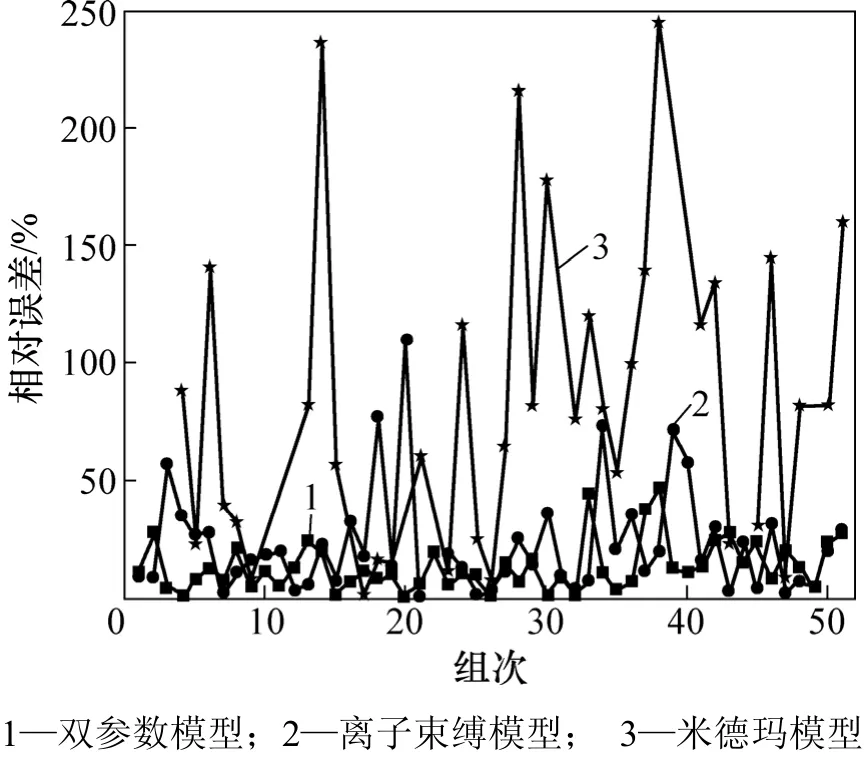
图3 3种模型的相对误差比较Fig.3 Comparisons of relative error of three models

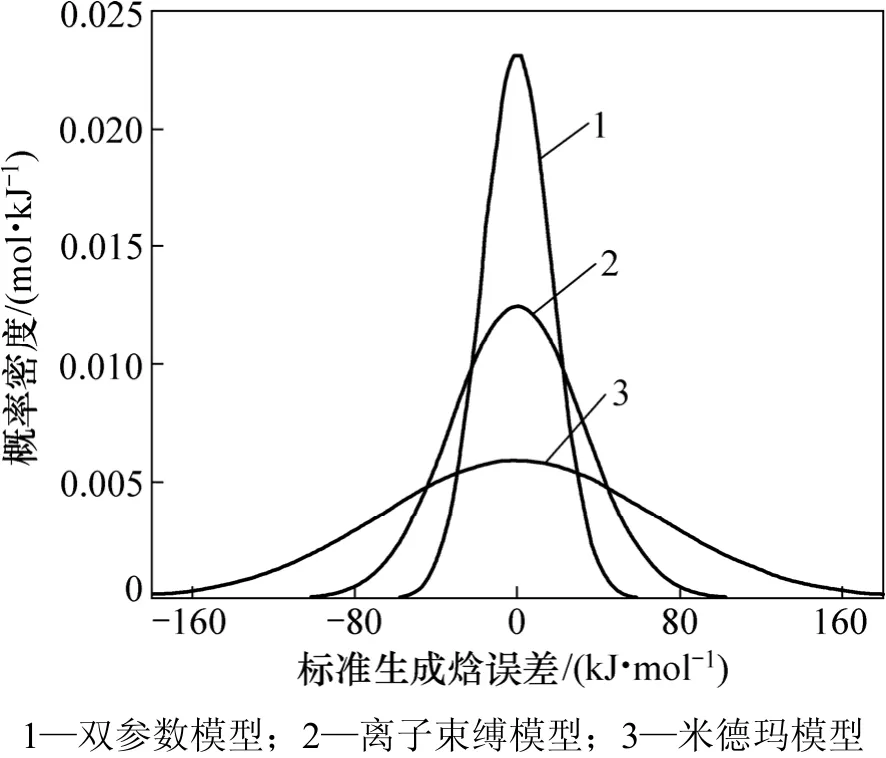
图4 硅系金属间化合物标准生成焓误差分布Fig.4 Error distributions of standard enthalpies of intermetallics containing silicon

4 结论

(1) 建立了金属间化合物的双参数模型，用来估算金属间化合物的标准生成焓。

(2) 利用双参数模型，估算的金属间化合物的平均误差为12.47 kJ/mol，相关系数为0.992，109个数据的标准差为17.40 kJ/mol。从统计学角度来看，双参数模型是可靠的。

(3) 双参数模型估算的标准生成焓要比离子束缚模型的标准差要小，其绝对误差和相对误差均比米德玛模型和离子束缚模型的小，指标比米德玛模型和离子束缚模型的优。

[1] 陈星秋, 严新林, 丁学勇, 等. 化合物生成焓：一百年和密度泛函基量子机制的原子模型新时代[J]. 中国稀土学报, 2004,22(增刊): 2-3.CHEN Xing-qiu, YAN Xin-lin, DING Xue-yong, et al.Enthalpies of formation for compounds: a century and comes of age for density functional based computations[J]. Journal of the Chinese Society of Rare Earth, 2004, 22(z1): 2-3.

[2] Latimer W M. Methods of estimating the entropies of solid compounds[J]. J Am Chem Soc, 1951, 73(4): 1480-1482.

[3] 汤振雷, 王为. 计算合金系统热力学性质的 Miedema模型的发展[J]. 材料导报, 2008, 22(3): 117-118.TANG Zhen-lei, WANG Wei. Review of Miedema model for calculating thermodynamic proper ties of alloys system[J].Materials Review, 2008, 22(3): 117-118.

[4] Ray P K, Akinc M, Kramer M J. Applications of an extended Miedema model for ternary alloys[J]. Journal of Alloys and Compounds, 2010, 489(2): 357-361.

[5] 乔芝郁, 许志宏, 刘洪霖. 冶金和材料计算物理化学[M]. 北京: 冶金工业出版社, 1999: 65-69.QIAO Zhi-yu, XU Zhi-hong, LIU Hong-lin. Computerized physical chemistry of metallurgy and materials[M]. Beijing:Metallurgical Industry Press, 1999: 65-69.

[6] 周鸿翼, 刘天模, 王金星. Mg-Zn合金的热力学性质计算[J].重庆大学学报, 2006, 29(12): 68-70.ZHOU Hong-yi, LIU Tian-mo, WANG Jin-xing. Calculation of the thermodynamic properties of Mg-Zn alloy[J]. Journal of Chongqing University, 2006, 29(12): 68-70.

[7] 郭培民, 赵沛. 用双参数模型估算复合氧化物的标准熵[J].钢铁研究学报, 2006, 18(9): 17-20.GUO Pei-min, ZHAO Pei. Estimation of standard entropy of complex oxide using two-parameter model[J]. Journal of Iron and Steel Research, 2006, 18(9): 17-20.

[8] 郭培民, 赵沛. 双参数模型预报复合氧化物的生成焓[J]. 钢铁研究学报, 2007, 19(5): 25-28.GUO Pei-min, ZHAO Pei. Estimation of standard enthalpies of complex oxide using two-parameter model[J]. Journal of Iron and Steel Research, 2007, 19(5): 25-28.

[9] 郭培民, 赵沛. 双参数模型估算复合氧化物比热的研究[J].钢铁研究学报, 2008, 20(8): 5-7.GUO Pei-min, ZHAO Pei. Estimation of specific heat of complex oxide using two-parameter model[J]. Journal of Iron and Steel Research, 2008, 20(8): 5-7.

[10] 赵定国, 郭培民, 赵沛. 金属间化合物的标准熵估算模型[J].北京科技大学学报, 2010, 32(1): 27-31.ZHAO Ding-guo, GUO Pei-min, Zhao Pei. Estimating model for standard entropy of intermetallics[J]. Journal of University of Science and Technology Beijing, 2010, 32(1): 27-31.

[11] 赵定国, 郭培民, 赵沛. 金属间化合物的比热容估算模型[J].北京科技大学学报, 2010, 32(5): 565-569.ZHAO Ding-guo, GUO Pei-min, ZHAO Pei. Estimating model for specific heat of intermetallics[J]. Journal of University of Science and Technology Beijing, 2010, 32(5): 565-569.

[12] 叶大伦, 胡建华. 实用无机物热力学数据手册[M]. 北京: 冶金工业出版社, 2002: 10-102.YE Da-lun, HU Jian-hua. Applied thermodynamics data of mineral inorganic substance[M]. Beijing: Metallurgical Industry Press, 2002: 10-102.

[13] David R L. CRC handbook of chemistry and physics 88th edition[M]. Boca Raton: Chemical Rubber Company Press, 2008:10-213.

[14] Dean J A. 兰氏化学手册[M]. 15版. 北京: 科学出版社, 2007:125-512.Dean J A. Lange’s chemistry handbook[M]. 15th ed. Beijing:Science Press, 2007: 125-512.

[15] Brain I. 纯物质热化学数据手册[M]. 北京: 科学出版社, 2003:1-188.Brain I. Thermochemical data of pure substances[M]. Beijing:Science Press, 2003: 1-188.

[16] 郑志刚. 合金热力学性质的Miedema理论计算[D]. 南宁: 广西大学资源与冶金学院, 2005: 6-9.ZHENG Zhi-gang. Calculation of thermodynamic properties of the multi-component alloys with Miedema theory[D]. Nanning:Guangxi University. College of Resources and Environment,2005: 6-9.

[17] WANG Wen-chao, LI Jia-hao, YAN Hua-feng, et al. A thermodynamic model proposed for calculating the standard formation enthalpies of ternary alloy systems[J]. Scripta Materialia, 2007, 56(11): 975-978.