运用统一强度理论分析预应力组合圆筒分层半径和过盈量
2011-05-28敖文刚
敖文刚,王 歆
(重庆工商大学机械工程学院,重庆 400067)
模具寿命是冷锻成形工艺的关键问题之一,增加模具强度就能显著地提高模具寿命。模具的强度提高通常是采用预应力组合模具结构,它是利用双层或多层厚壁圆筒过盈配合所产生的预应力来达到的。如何确定预应力组合模具的分层半径和过盈量是组合圆筒分析的重要问题,对此的一个基本原则就是要提高组合圆筒内外筒(预应力圈和凹模)同时达到弹性极限的取值。在弹性力学中,对组合厚壁圆筒的分析一般情况下采用了Tresca屈服准则,但是Tresca屈服准则不考虑材料拉压异性和中间应力对材料屈服的影响,所以Tresca屈服准则只能使用于拉压强度相等且τS=0.5σS的材料,运用统一强度理论进行分析的结果对其他材料均可适用。
1 统一强度理论
双剪统一强度理论[1]定义为:当作用于双剪单元体上的两个较大剪应力及其相应的正应力函数达到某一极限值时,材料开始发生破坏。双剪统一强度理论在主应力空间的数学表达式为

2 组合厚壁圆筒分析
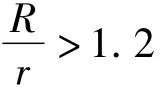
2.1 厚壁圆筒弹性分析
结构荷载较小时,圆筒处于弹性状态,对厚壁圆筒的讨论将从弹性分析开始。在进行分析时,采用极坐标(ρ,θ)表示各分量。由于轴对称性,τρθ=0,径向应力与切向应力仅是 ρ的函数,即 σθ(ρ)和 σρ(ρ)。对外径为R,内径为r的厚壁圆筒,在内压p1和外压p2的作用下,通过应力法进行弹性分析可以得到其应力分量为[4]:

这就是拉梅公式,它和弹性常数无关,可以适用于两类平面问题。这里可以考虑两种均压作用下的结果。
(1)只有均匀内压p1,即p2=0,应力分量为:

(2)只有均匀外压p2,即p1=0,应力分量为:

2.2 运用统一强度理论确定厚壁圆筒屈服条件

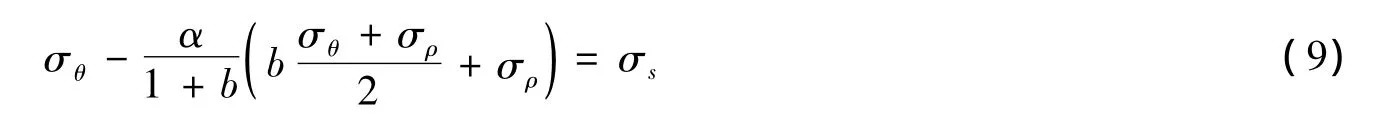
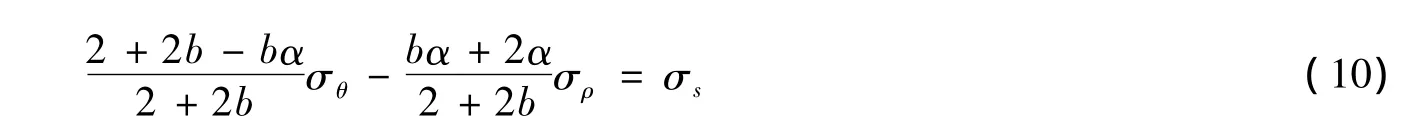
将式(9)化简为:这就是统一强度理论用于厚壁圆筒而得到的判断材料屈服的条件[1]。
2.3 组合厚壁圆筒分层半径与过盈量分析
首先,设定内半径为r,外半径为R的组合圆筒是由两层圆筒套装而成,内筒的内半径为r,外半径为r1+δ1,外筒的内半径为r1-δ2,外半径为R,并设两圆筒材料相同。这样的内外圆筒套装后可知内外筒间会产生套装压力,根据弹性力学可得到其表达式为[4]:式中δ=δ2-δ1为过盈量,E'为平面应变条件下的弹性模量。在套装压力作用下,组合筒体内就会产生套装应力,它是预应力,将与筒体受均匀内压作用后产生的应力进行叠加。

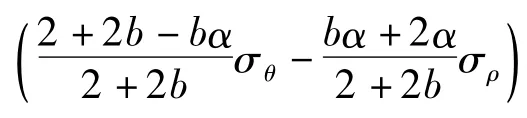
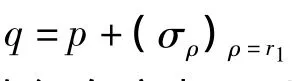

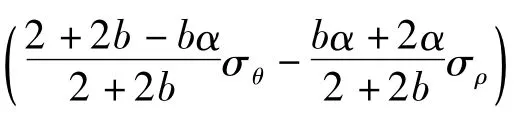

为了得到最优结果有:

则可求得:
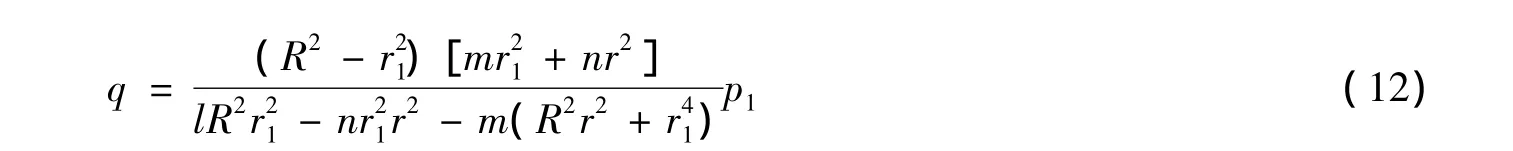
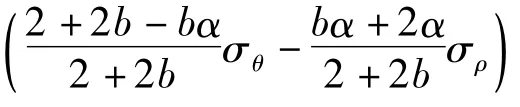
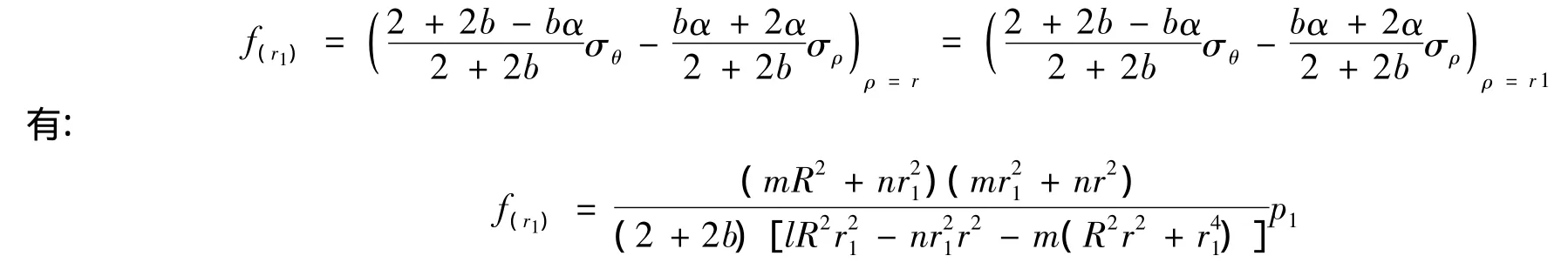



此时的套装压力p=q-(σρ)ρ=r1可计算得到:
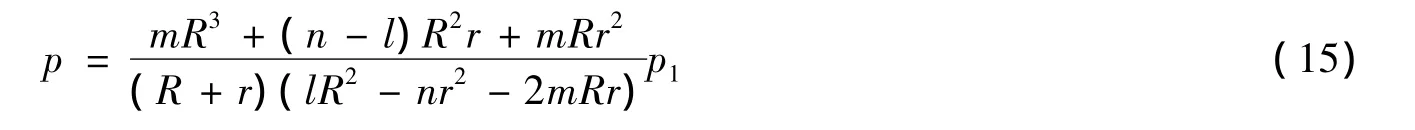
根据套装压力与过盈量的关系,把式(13)(15)代入式(11),可得到:
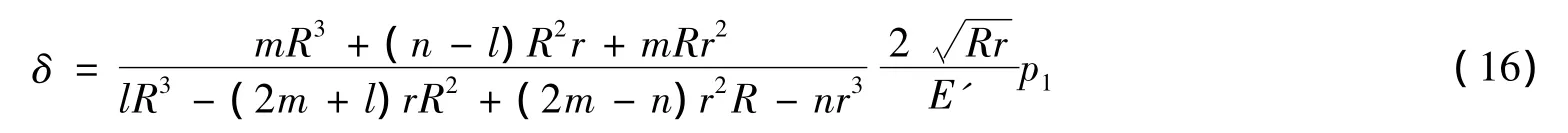

但在α≠1时,过盈量δ的计算应该按式(16)计算,必须考虑参数b和组合圆筒内外径的综合影响。假设R=2r和R=3r的情况下,分别取 α =0.8、0.6、0.4、b=1、0.5、0 时,计算过盈量 δ的值,得到表 1、表2 所示的结果。

表1 R=2r时过盈量δ的取值

表2 R=3r时过盈量δ的取值
3 实例分析
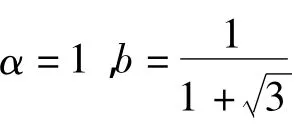

图1 组合凹模Mises等效应力云图

图2 组合凹模Mises等效应力曲线
从上述分析可以看出,根据公式计算出来的分层半径、材料许用应力、过盈量可使凹模和预应力圈同时达到材料的许用应力,最大程度的发挥了预应力圈和凹模材料的强度潜能。
4 结论
运用统一强度理论来分析的组合圆筒的分层半径r1=■Rr,它仅与组合圆筒的内外径相关,而与材料的特性无关,所以分层半径计算是组合圆筒自身确定的,与屈服条件的选择无关。用统一强度理论来分析的组合圆筒的过盈量不仅与组合圆筒的内外径相关,也与材料的特性相关,所以过盈量δ的计算不仅考虑组合圆筒的内外径尺寸,还要根据材料特性考虑屈服条件的选择。
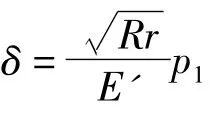
[1]俞茂宏.工程强度理论[M].北京:高等教育出版社,1997.
[2]高汉华.转子挤压组合凹模的应力分析[J].模具技术,2006,23(1):33-35
[3]敖文刚.双剪统一强度理论在厚壁圆筒分析中的应用[J].模具工业,2007,33(8):28-31
[4]徐秉业,刘信声.应用弹塑性力学[M].北京:清华大学出版社,1995.
