关于机器人足球视觉系统中场地标定方法综述

刘婵桢

（重庆理工大学计算机科学与工程学院，重庆 400050）

足球机器人系统是一个涉及计算机视觉、人工智能、无线通信和自动控制等多种领域的典型的智能机器人系统。其中视觉系统是机器人足球的最前端系统，负责原始的球场信息的采集工作，相当于足球机器人的眼睛，因此，“眼睛”的误差将直接影响整个系统精确和稳定，而摄像机的标定是视觉系统处理的第一步，是整个视觉系统的基础。摄像机标定是指建立摄像机图像像素位置与场景点位置之间的关系，其途径是根据摄像机模型，由已知标定点的图像坐标和世界坐标求解摄像机的模参数［1］。摄像机透视模型分为线性模型与非线性模型。因此标定方法分为线性的与非线性的。国内外在机器人足球视觉标定方面做了大量的研究，并提出一些可行的方法。对摄像机成像的几何模型和光学畸变进行了详细的分析，并分别阐述了相关的研究思路和方法，为机器人足球视觉系统的研究提供了参考。

1 基于摄像机成像的几何模型的标定方法

1.1 采用线性模型求解摄像机参数

线性摄像机的建模涉及到3个坐标系:图像坐标系、摄像机坐标系和空间坐标系。

理想的透镜成像是针孔模型，如图1所示。

其中，Oc－XcYcZc为摄像机坐标系，其原点Oc即为摄像机的光心，Zc轴与光轴重合。Ow－XwYwZw为世界坐标系，O－xy为图像物理坐标系，坐标原点在光轴与图像平面的交点为O，其x，y轴分别平行于摄像机坐标系的Xc，Yc轴。O－uv为图像像素坐标系，（Xw，Yw，Zw）是三维世界坐标系中物体点P的三维坐标，（u，v）是计算机图像坐标系中空间任意一点P点的成像点p的实际图像坐标，单位是像素数（pixe1）。焦距f为图像平面到光学中心的距离。

采用线性模型［2］，对于选定的n个特征点，有2n个关于计算参数矩阵M元素的方程，用矩阵形式表示为:

图1 理想的摄像机模型

1.2 改进的线性标定方法

方法是一种基于标志点将场地分区的线性标定算法。具体的算法如下:通过拖动鼠标在图像上确定一个矩形，4 个顶点分别为A、B、C和D，其分别对应的世界坐标为A（0，0），B（0，180），C（220，180），D（220，0）;A，B两点之间屏幕坐标Y之间的差值与A，B两点之间世界坐标Y之间的对应关系为;A，D两点之间的屏幕坐标X之间的差值与A，D两点之间的世界坐标X之间对应关系为。

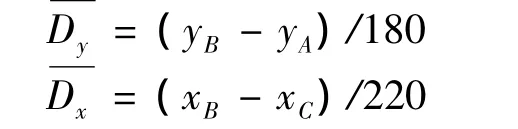
线性标定方法，只需求解线性方程，简单快速，原理简单，实现容易。改进的线性标定方法一般根据经验对场地分区，在每个分区中，分块对场地进行标定，同时对边界进行处理。改进的标定方法相对于前一种线性标定方法，在一定范围内缩小误差。但线性模型不考虑镜头畸变，准确性欠佳，精度不高。

2 基于摄像机光学畸变的标定方法

2.1 求解畸变的各种数学模型

引入非线性畸变的数学模型主要有以下几种:

（1）仅考虑镜头的径向畸变时，可得到镜头几何畸变修正的数学模型为［3］:

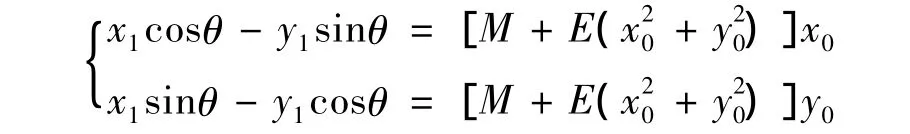
其中θ为畸变前后的坐标系偏转角。

（2）对足球机器人视觉系统中采用的短焦广角镜头可建立只考虑径向误差的数学模型，在实际应用中，为了减少运算量，在不影响畸变校正效果的前提下，忽视其径向误差中的高次项，镜头误差表达式可以简化为［4］:

其中ρ2=（x－x0）（y－y0），k1为径向畸变系数，（x0，y0）是成像面中心点的坐标。

（3）图像的非线性几何畸变可用坐标间的多项式来表示。令（x，y）为无畸变图像上任一点的坐标，（xd，yd）为畸变图像上与（x，y）相对应的点坐标。则有关系式［5］:

式中:aij，bij为多项式的系数;n为多项式的次数。按最小二乘法，通过求解使得拟合误差平方和最小时的aij，bij，即可求出校正前后坐标点之间的变换关系。

2.2 基于神经网络的标定方法

（1）BP网络。用于摄像机标定的BP网络的结构如图2所示［7］。根据摄像机标定的特点，网络输入为标定样本点的图像像素坐标（u，v），输出为其对应的世界坐标（X，Y），即BP网络为2－n－2结构。n为网络的隐层节点数。

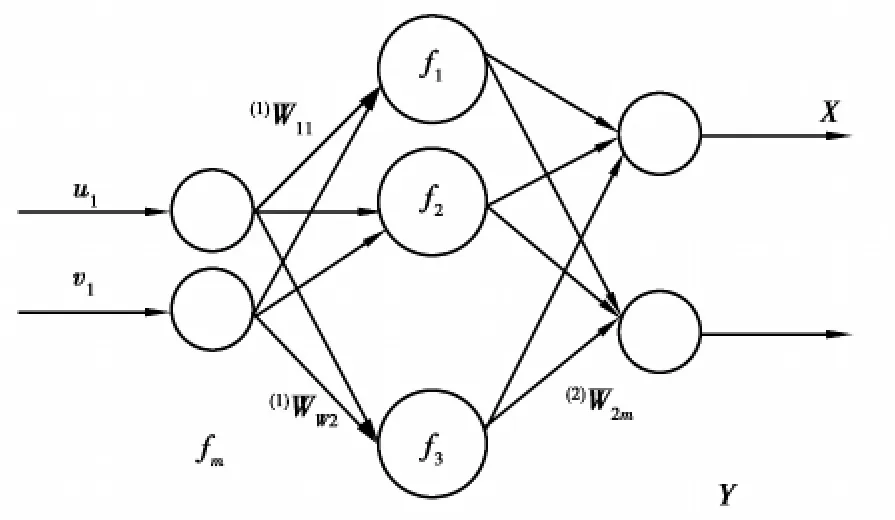
图2 单目标定的BP网络结构

（2）RBF网络。从理论上讲，RBF网络和BP网络一样可近似任何的连续非线形函数，两者的主要差别在于各使用不同的作用函数，BP网络中的隐层节点使用的是Sigmoid函数，其函数值在输入空间中无限大的范围内为非零值，而RBF网络的作用函数则是局部的。

BP网络和RBF网络是两种应用颇为广泛的神经网络模型。在解决具有相同精度要求的问题时，BP网络的结构要比RBF网络简单，但在逼近能力，收敛速度以及搜索的遍历性等方面RBF网络都优于BP网络［6］。在机器人足球视觉系统场地标定中，BP网络实现起来比RBF网络简单，但RBF网络能够实时及准确地得到更精确的机器人位置。

3 发展与展望

用线性模型进行场地标定的方法简单快速，可靠性高;但方法假定图像上的直线经过透视投影仍然为直线，未考虑摄像机光学系统中存在的加工误差和装配误差，实际上引入了误差，经实验，在边界畸变较大的情况下，校正的效果较差。对场地分区或引入畸变参数可以提高场地标定精度。引入畸变参数时，从不同的模型出发可得到不同的方法，神经网络模型因为其可以逼近任意非线性函数的特点，因而作为一种新的模型应用在视觉系统的场地标定中。数学模型的建立提高场地标定的精度，但计算量大，比较繁琐;而神经网络这种新型模型在保证精度的前提下摆脱了繁琐，但实时性有待进一步提高。

随着广角镜头的广泛使用以及各种技术不断地发展和成熟，视觉系统中的场地标定精度有待进一步提高，且具有很大的发展潜力。建立合理可靠的模型是提高场地标定精度的重要途径。

［1］张广军.机器视觉［M］.北京:科学出版社，2005

［2］马颂德，张正友.计算机视觉—计算理论与算法基础［M］.北京:科学出版社，2003

［3］王婷婷，王朝辉.机器人足球视觉系统图像畸变的几何校正［J］.贵州工业大学学报，2007，36（1）:56-59

［4］邓梅生.光学理论与实践［M］.武汉:武汉大学出版社，2004

［5］吴佩杰，张奇志.MiroSot机器人足球视觉系统图象畸变的几何校正［J］.北京机械工业学院学报，2008，24:49-52

［6］MUSAVI M T.On the training of the radial basis function classifiers［J］.Neural Networks.1992（5）:595-603

［7］宗晓萍，石圣羽，田华.基于BP神经网络的足球机器人摄像机标定［J］.计算机工程与应用，2007，44（8）:204-206

［8］袁野，田中旭，欧宗瑛.应用径向基函数网络进行足球机器人视觉系统的标定［J］.计算机工程与应用，2003，65:89-91