股票价格遵循O-U过程的几何型亚式期权定价*

刘兆鹏，张增林

（宿州学院数学与统计学院，安徽宿州 234000）

亚式期权是当今金融衍生品市场上交易最为活跃的新型期权之一。它与标准的欧式期权不完全相同，其在期权到期日的收益不仅取决于标的资产到期日的价格，还依赖于在整个期权有效期内原生资产所经历的价格平均值。一种为算术平均;另一种为几何平均。亚式期权是一种强路径有关期权，相对于标准欧式期权，亚式期权比较便宜，对某些公司更有吸引力，它在许多金融领域有着广泛的应用，因此其定价也具有重要意义［1－3］。此处选择能反映股票预期收益率波动变化的指数O－U过程来刻画股票价格的变化规律，利用等价鞅测度法，给出了具有固定执行价格的几何型亚式期权的精确定价公式。

1 亚式期权定价模型

考虑一个连续时间无套利的完备金融市场，假定市场存在两种资产:一种是无风险资产，如债券;另一种是风险资产（或股票）。给定一个满足通常条件滤子流{Ft}t≥0的完备概率空间（Ω，F，（Ft）t≥0，P）。

股票价格过程S（t）遵循广义O-U过程:

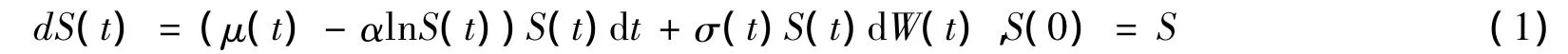
其中σ（t）为股票的波动率，μ（t）为股票的期望回报率，μ（t）和σ（t）充分光滑使得方程（1）有严格唯一正解，并且S＞0，α 为常数。{W（t），0≤t≤T}是定义（Ω，F，（Ft）t≥0，P）在上的标准 Brown 运动。

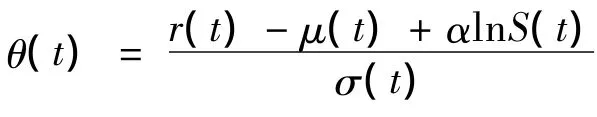
测度Q下WQ（t）是一个Brown运动，且股票的价格过程S（t）满足

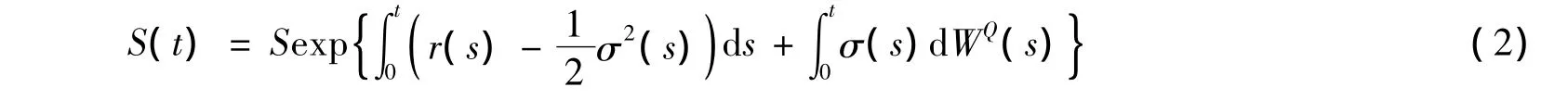
1981年Harrison.J.M和Pliska引进了自筹资复制的概念，证明了如果等价鞅测度存在且唯一，则市场是完备的无套利市场，这时市场的任何衍生证券都可由市场上用于交易的基础证券的自筹资投资组合完全复制，并且任何衍生证券都有唯一的合理价格，该合理价格为衍生证券的贴现收益关于等价鞅测度的数学期望［5－7］。对指数O-U过程模型，可以证明市场模型是完备的无套利市场［8］。

2 指数O-U过程模型下几何型亚式期权的鞅定价

定理1 具有固定执行价格的几何平均亚式看涨期权的定价公式为:

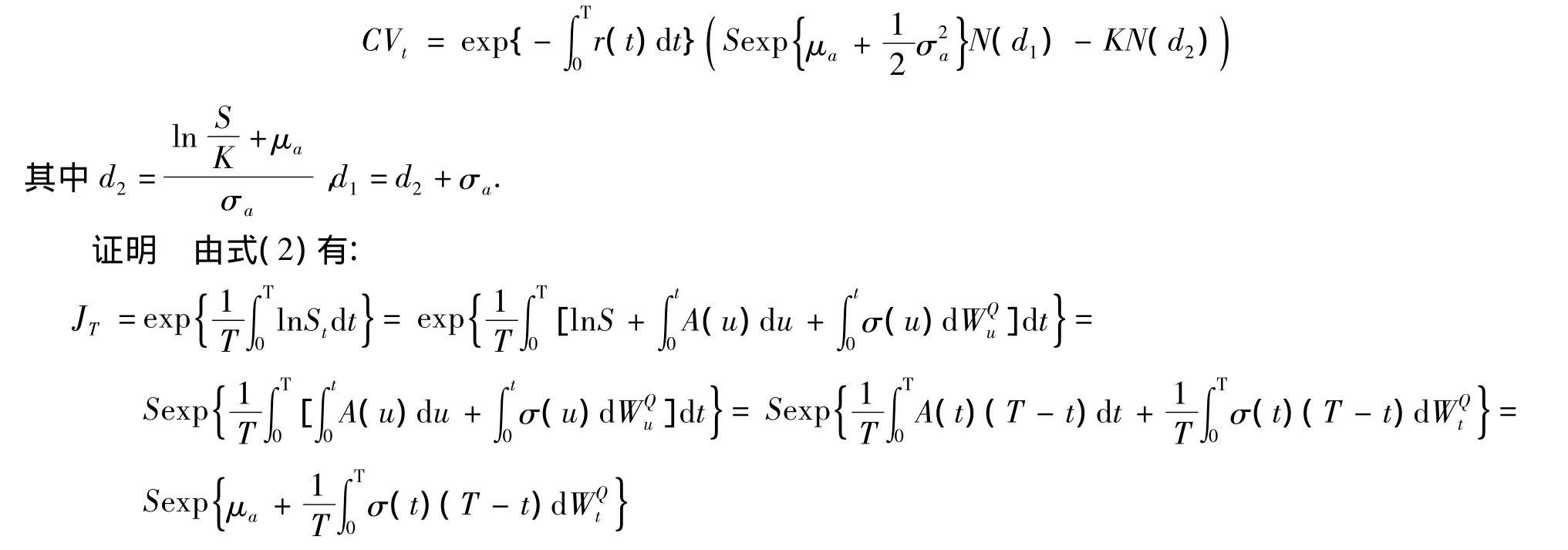
最后一个等式是通过交换二重积分的积分顺序而得到的。所以

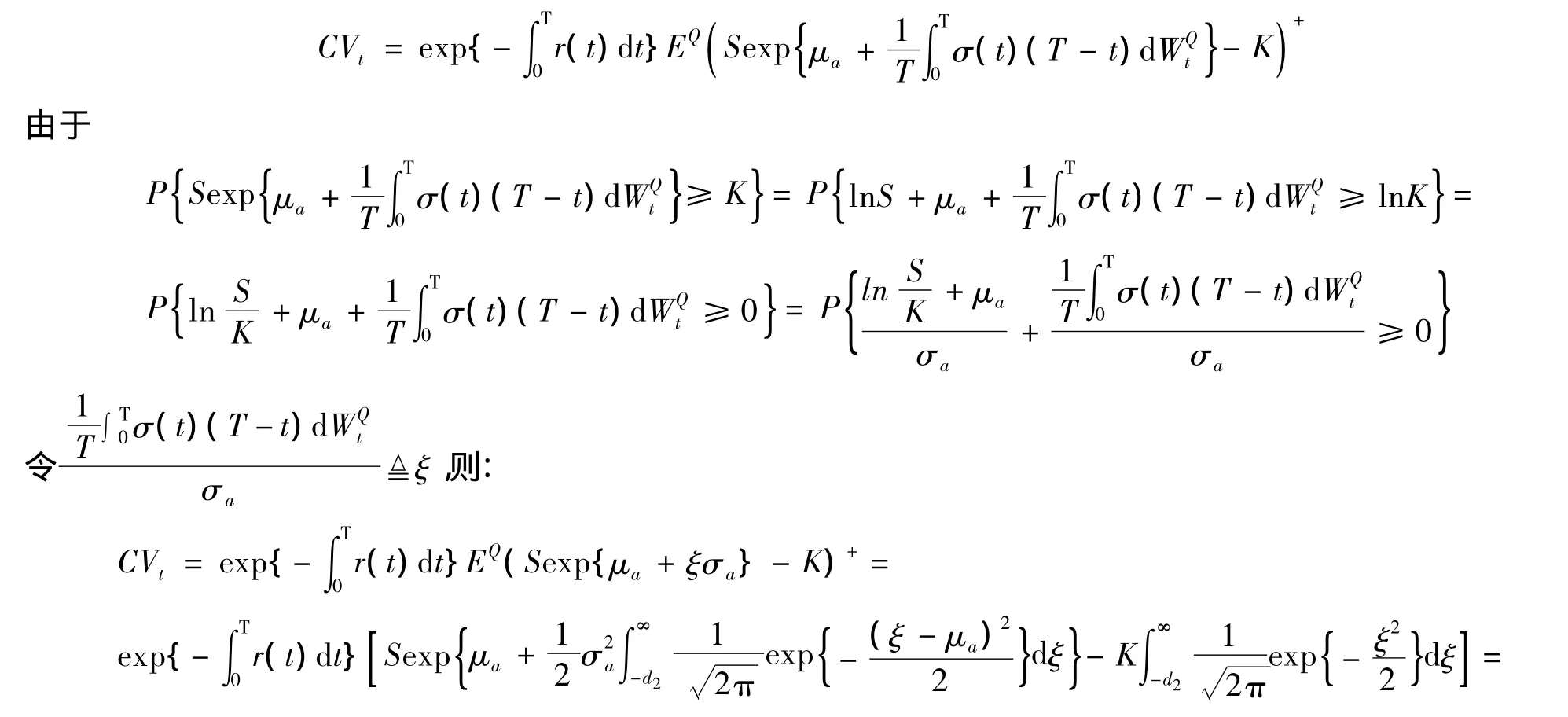
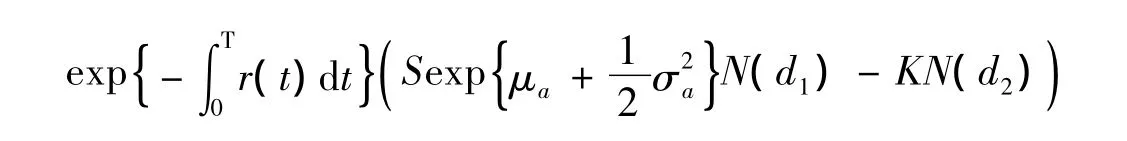
可以用同样的证明方法得到如下定理。

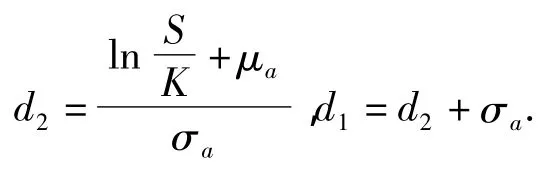
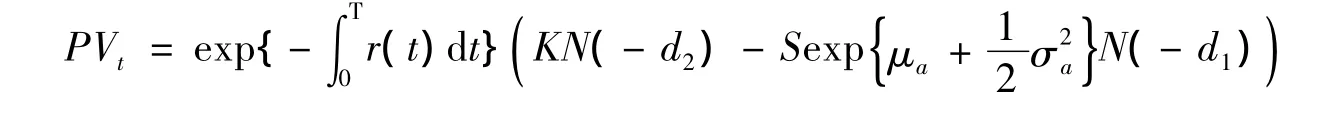
其中

3 结束语

在假定股票价格服从指数O-U过程模型的条件下，用鞅方法得出几何型亚式期权定价公式，结果是对经典Black-Scholes模型的推广，使得定价模型更符合现实的金融市场，为衍生品市场参与各方投资决策提供科学的理论依据。同时，也为金融市场的不断创新开辟新的思路，符合当前证券市场发展的需要，对提升证券公司经营的竞争力和风险管理水平具有重要的现实意义。

［1］詹惠蓉，程乾生.亚式期权在依赖时间的参数下的定价［J］.管理科学学报，2004，7（6）:24-29

［2］章珂，周文彪，沈荣芳.几何平均亚式期权的定价方法［J］.同济大学学报，2001，29（8）:924-927

［3］罗庆红，杨向群.几何型亚式期权的定价研究［J］.湖南文理学院学报，2007，19（1）:5-7

［4］闫海峰，刘三阳，李文强.股票价格遵循指数O-U过程的最大值期权定价［J］.工程数学学报，2004，21（3）:397-402

［5］LAMBERTON D，LAPEYRE B.Introduction to Stochastic CalculusApplied to Finance［M］.New York:Chapman ＆ Hall，1996

［6］HARRISON J M，PLISKA S R.Martingale and Stochastic Integrals in the Theory of Continuous Trading［J］.Stochastic processes and their applications，1981，11（2）:215-260

［7］郑晓阳，刘兆鹏.基于O-U过程的具有不确定执行价格的期权定价［J］.哈尔滨工程大学学报，2008，29（11）:1232-1235

［8］李春泉，刘新平.Black-Scholes模型期权定价方法及其应用［J］.重庆工商大学学报:自然科学版，2006，23（4）:351-353