信号与系统的教学实例:基带传输中的码间干扰
2011-05-28翁剑枫郑卫红
翁剑枫,郑卫红
(浙江科技学院信息与电子工程学院,杭州310023)
信号与系统课程是电子信息类专业的一门重要的专业基础课,所涉及的基本理论和分析方法构成了后续的数字信号处理、通信原理等课程的先修基础知识,也是学生在毕业设计及日后工作中的重要基础。
为了使学生更好地掌握这门课程的基本原理和基本概念,有机地建立起重要概念之间的联系,应该在讲解原理、概念的同时,尽早地引入与之密切相关的应用实例分析。因此,笔者主张在介绍完时域、频域分析的基本理论后,围绕傅里叶变换应用的中心议题,从后续课程中挑选一些实例,通过对这些实例的分析,既使学生加深对基本概念的理解,也使学生受到将基本理论和分析工具用于工程实践的训练。
本文将就教学实践中所采用的一个实例——数字基带传输中的码间干扰[1]作一教学分析。码间干扰问题中,涉及信号与系统课程中的许多极为重要的概念,包括信号带宽与系统带宽的匹配问题、不失真传输、采样与重建及系统的物理可实现性[2-4]等。几年来的教学实践证明,通过这个实例,既可使学生更好地理解以上这些信号与系统分析的重要概念,也可使学生在随后的通信原理课程学习中,较好地克服以往学习数字基带传输中码间干扰时所遇到的困难。
需要指出的是,作为技术基础课程,这里的教学与专业课教学有明显的区别[5]。本文在分析中并不涉及工程实际的具体细节,而是着重就问题所涉及的基本概念进行分析,也即着重于概念与应用的结合这一层面,为学生构筑从基础理论步入工程专业课程学习的桥梁。
1 数字基带信号通过限带基带信道的传输
数字传输技术已经在绝大多数应用场合下替代了模拟传输,在图1所示的数字基带传输系统中,信源输出的消息(或符号)不再是模拟信号本身,而是将模拟信号进行采样和量化编码后的一个二进制比特流,通常用二进制数字序列{dn}表示,其中 dn为1或0。

图1 数字基带传输系统Fig.1 Digital base-band transmission system

图2 发送滤波器的功能示意图Fig.2 diagram of transmitting filter
图2示出的x(t)是以脉冲载波幅度携带数字信息的信号,每一个波形脉冲都是时限信号,因此从信号分析角度来说具有无限带宽。另一方面,实际数字通信中的信道都是限带的,如常用的电话信道或移动通信信道,都只有有限带宽,从系统分析角度说,这样的信道是一个有限带宽的线性系统。因此就出现了信号带宽与系统带宽无法匹配的问题[2-4]。
从信号通过系统的角度说,具有无限带宽的基带脉冲信号通过上述有限带宽的线性系统传输后,由于受到信道带宽的限制,必然无法实现不失真传输,也即会引入失真。这种失真通常主要表现为信号展宽。这样,在图1中的接收滤波器输出处,相应时刻进行采样得到的采样值并不完全由该时刻的信号所决定,其中还必然存在着信源在其他时刻发送过来的信号的贡献[2-4]。正因为此,这一现象被称为码间干扰(ISI,inter-symbol interference),其后果是接收端不能从这些采样值中正确地解析出信源发送来的信息。因此在实际应用中,必须首先弄清码间干扰的来源,进而设法消除或尽可能地减小码间干扰。而这两个问题涉及了信号与系统课程中的许多极为重要的概念,因而在信号与系统课程中提早引入这一论题作为应用实例,既有助于学生对基本概念的理解掌握,也有助于学生接受将基本原理运用于工程实际问题的训练[6-7]。
2 码间干扰的来源
数字传输系统中,信源输出的二进制比特流经发送成型滤波器的输出波形信号,经过信道C(jω)传输到接收滤波器GR(jω),在不计信道噪声时,接收滤波器的输出可以写为:

其中h(t)是发送成型滤波器GT(jω)、信道C(jω)、接收滤波器GR(jω)串联组成的合成系统的单位冲激响应,这个串联系统的频率特性为

由此,图1所示的数字基带传输系统现可等效地表示为图3所示的系统。

图3 数字基带传输系统的另一种表示Fig.3 Another representation of digital base-band transmission system
与模拟传输不同,对于数字传输而言,接收端需要进行的工作不是获取不失真的发送端波形,而是要得到相应时刻信源发来的二进制数字信息。为此,需要对接收到的信号y(t)进行采样,然后进行判决。为分析方便,不失一般性,忽略h(t)引入的传输延迟t0,因此可认为在t=kT时进行采样即能得到该时刻由信源发出的信息:
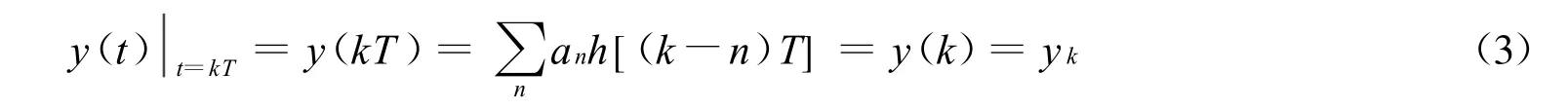
在t=kT时,信源发出的是与d k相应的a k,因此希望采样得到的yk等于a k,但在实际上,除了ak以外,yk中还包含了干扰:
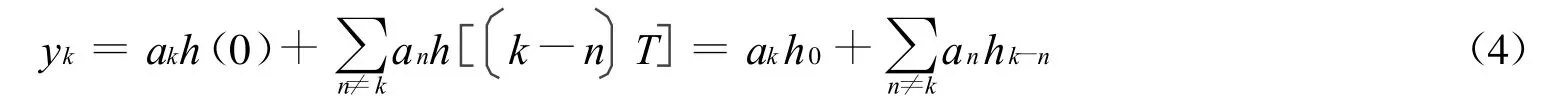
式(4)表明,yk由两部分组成,一部分是希望得到的akh 0,这里h0是常数,不妨设h0=1,而另一部分就是干扰。由干扰的表达式可以知道,干扰中的各项都来自于其他时刻信源发出的信息,故称之为符号间干扰,也称为码间干扰。
3 码间干扰的消除


能够满足这一特性的有限带宽系统并不是唯一的,其中最简单的是采样与重建中重点分析过的带宽等于(rad/s)的理想低通滤波器[2-4],它的单位冲激响应是:相应的 H(jω)=GT(jω)C(jω)GR(jω)的系统带宽为(rad/s),也即(Hz)。也就是说,如果由发送 成型滤波器GT(jω)、信道 C(jω)、接收滤波器 GR(jω)串联组成的合成系统 H(jω)是一个带宽等于(rad/s)的理想低通滤波器,则从理论上来说,码间干扰就可以被消除。但在实际应用中这样的H(jω)是不能使用的。其原因为:首先,所对应的单位冲激响应h(t)的尾部下降速率较慢,在t→+∞过程中,仅以的速率趋于零,因此,如果采样时刻的定时稍有偏差,中各项就不能严格为零,从而其累积叠加仍会使码间干扰发生。而在实际情况下,采样时刻的随机抖动是不可避免的。其次,由于理想滤波器的单位冲激响应h(t)具有无限时长,是物理上不可实现的。因此,在实际应用中,这样的H(jω)是无法构成的。
所以,为了消除码间干扰,H(jω)=GT(jω)C(jω)GR(jω)对应的 h(t)除了必须满足式(5)所示的条件外,还应具有较快的尾部衰减速率,以克服实际采样中发生的定时不准确所带来的问题,并可以近似视为具有有限时长,从而具有物理上的可实现性[2-4]。
工程实际中,最为广泛使用的方法是对h(t)使用下面形式的衰减因子:

式(7)中α的取值范围为0≤α≤1。由于这个衰减因子随t→+∞的衰减速率为,且随α的增大而衰减加快,因此在α取值较大时,这个衰减因子能够大大减小由于采样定时不准确造成的累积干扰效应,从而能够有效地消除码间干扰。
这样,在对由式(6)所示的h(t)引入式(7)所示的衰减因子后,也即将式(6)、式(7)相乘后,就可既满足式(5)的要求,又可引进较快的尾部衰减。而根据频域卷积定理,相应的H(jω)可通过将理想低通滤波器的傅立叶变换与衰减因子的傅立叶变换进行卷积得到。工程中,通常称这样得到的信道频谱特性为升余弦频谱特性。
由于合成的传输信道的单位冲激响应的尾部衰减更快,码间干扰将被大大减小。但在实际工程中,为获得某种得益,通常必须在其他方面付出代价。进一步的分析表明,对于消除码间干扰而言,所必须付出的代价是,对于相同的T,也即相同的数据传输率,必须使用更大的H(jω)带宽,也即传输信道的带宽必须增大。在实际工程应用中,这种性能与代价的交换是常见的,为了提高某些性能,必然需要付出某种代价,因此往往要在两者之间进行权衡和折中。
在 H(jω)=GT(jω)C(jω)GR(jω)采用了升余弦频谱特性后,相应的时域波形尾部衰减很快,因此经过几个 T后就可以将其截断而不会产生实质性的影响,从而可以使发送滤波器对每个二进制字符所赋予的输出波形成为物理上可实现的有限长波形,这样就能真正用于实际情况[2-4]。
4 结 语
从以上分析可见,数字基带传输中码间干扰的产生与消除问题,涉及了信号与系统分析中的一些最为重要的基本概念、基本原理和分析方法,非常适宜作为电子信息类专业信号与系统课程中傅里叶变换应用的综合性实例。即使对非电子信息类专业,只需在问题的提法和交待上略作改变,例如直接从图3开始展开,也是一个能够用于说明一些非常重要的基本概念(包括信号带宽与系统带宽的匹配问题、不失真传输、采样与重建及系统的物理可实现性等概念)的很好实例。几年来的教学实践表明,这种从后续专业课程中遴选出适合用于基础理论课程的应用实例的做法,比现有教材中人为设计编写的例题更为有效。通过对工程实际中萃取出来的应用实例的讨论、分析与讲解,能够让学生对所学到的基本概念、基本原理和分析方法受到综合性的训练,建立起各种概念之间的有机联系,并使学生初步受到将基本理论用于工程实际问题的体验和训练。此外,本文所述的“基带传输中的码间干扰”内容本身是通信原理课程中的教学难点,由于学时限制,在通信原理课程教学中,难以对此问题所涉及的重要概念和基本理论展开深入的分析。笔者将此问题作为信号与系统课程的应用实例进行充分的讨论、分析及讲解后,学生在通信原理课程学习中,就能够比较容易地理解掌握在此基础上得到的奈奎斯特准则了。因此,这一做法对电子信息类专业的后续课程教学也是有利的。
随着知识的发展,大学教学也必须随之变革,作为教师,希望自己的学生能够在大学的学习期间学到最有用的知识,构成最合理的知识结构,培养得到进一步获取知识的能力。笔者进行的教学探索还是非常初步的,甚至是微不足道的,之所以不揣冒昧将这点探索体会成文,最希望的是能够得到前辈的指教及同行们的指正。
[1] SKLAR B.数字通信——基础与应用[M].2版.影印版.北京:电子工业出版社,2002.
[2] 郑君里,应启珩,杨为理,等.信号与系统上册[M].2版.北京:高等教育出版社,2000.
[3] 吴大正.信号与线性系统分析[M].4版.北京:高等教育出版社,2005.
[4] 管致中,夏恭恪.信号与线性系统[M].3版.北京:高等教育出版社,1992.
[5] 郑君里.教与写的记忆:信号与系统评注[M].北京:高等教育出版社,2005.
[6] 张顺岚,莫建文,欧阳宁,等.基于问题的教学在信号与系统中的应用[J].桂林电子科技大学学报,2008,28(2):137-139.
[7] 姚青,童基均,陈淑敏,等.通信工程专业信号系列课程教学方法的探讨[J].浙江理工大学学报,2009,26(3):446-450.
