实现高效率的物流敏捷调运研究

王富忠

(浙江科技学院经济管理学院,杭州310023)

针对物流调运问题,近年来涌现出相当多的研究成果,其主要的研究方向聚焦于VRP(vehicle routing problem,车辆路径问题)、VSP(vehicle scheduling problem,车辆调度问题)[1-3]。国外在这些领域的研究已经比较成熟,国内在该领域的研究虽然起步相对较晚,但也涌现出了一大批的研究成果。例如,在该领域的研究文献已有200余篇,比较有代表性的是李军、郭耀煌的国家自然科学基金项目研究成果[4]。笔者通过对现有的研究文献进行梳理后发现,在现有的研究文献中,很少有针对物流调运问题提出相关的知识准则以提升物流调运的敏捷性这方面的研究成果[5]。基于此,本研究针对物流市场动态多变和物流运输资源(车辆)具有动态性的特点,特将物流调运者的实际工作经验和物流调运优化研究者的成果有机地结合起来,建立了有效的“敏捷调运知识准则”,从而在知识层面上,对物流敏捷调运优化方案的灵敏、快捷生成和实施给予有效的支持。虽然在以往的研究中已有少量文献通过研究归纳出几类与物流调运紧密相关的敏捷性知识准则[6-7],但这些文献中的每一类敏捷性知识准则的构建都是针对某类实际的运输调度问题的。在文献[6]和文献[7]的研究中,研究者利用敏捷性知识准则,在研究具体的调运问题时获得了下述的调运效果,如表1所示。

表1 各文献使用敏捷性知识准则后的调运效果Table 1 Scheduling effect used by agile knowledge rules of many references

在表1中,虽然各文献在使用敏捷性知识准则后的优势相当明显,但各自都存在一定的问题。为解决上述各文献中存在的缺陷,本文将在文献[6-7]的研究基础上,对如何实现高效率的物流敏捷调运问题进行研究。

1 问题背景与敏捷调运知识准则

1.1 问题背景

记配送中心标记为O,配送地记为h,距离记为d。本研究在实际问题的基础上,对配送货物进行归纳和简化后的一组实际数据如表2和表3所示,其中,车辆数据为模拟数据。

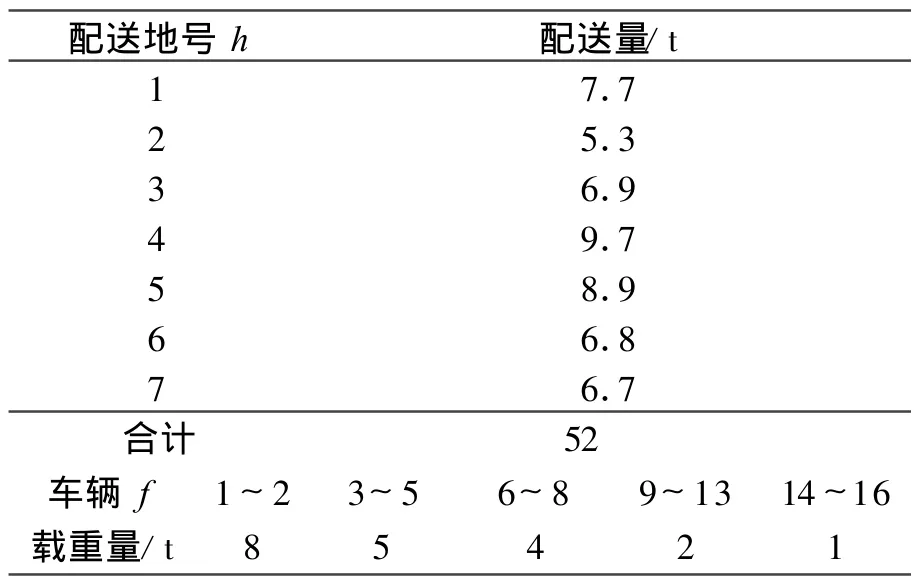
表2 货物配送需求量及车辆信息Table 2 Distribution demand number of goods and vehicles information

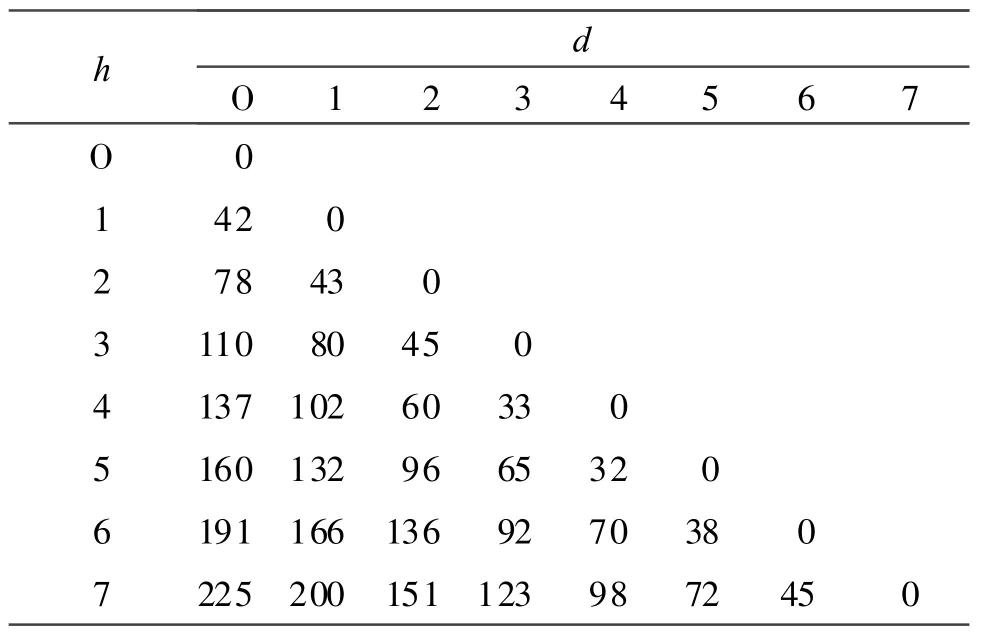
表3 距离信息表Table 3 Distance information

在考虑配送量与距离等因素的情况下,如何做到装载率的优化与成本的节约是本研究需要重点探讨的问题。

1.2 敏捷调运知识准则

为了实现物流调运的敏捷化,同时考虑到紧急调运情况、拼货情况、装载率最大化约束等情况,本研究在文献[7]的基础上对敏捷调运知识准则进行了完善:

第一优先准则 交货需求早并且满足拼货条件的配送地要优先安排装载。

第二优先准则 在考虑货物种类的情况下,对距配送中心远的配送地优先安排装载。

第三优先准则 在装载能力相同且有多种车辆组合可选情况下,尽可能选择配送车辆吨位大的优先安排装载。

第四优先准则 针对确定车辆装载物品重量大的优先安排装载。

在考虑4条知识准则的同时,采用就近插入法对线路进行优化。

与文献[7]相比,本研究采用就近插入法对线路进行优化,其方式是针对已确定要装载的车辆,并且这些车辆装载货物的目的地已经确定,在此基础上,由于存在多条线路可选,进而会影响到货运周转量。因此,在对这些车辆装货的同时,以降低货运周转量为内在条件对这些车辆的路线进行优化。

2 基于敏捷调运知识准则的车辆调度研究

2.1 车辆调运优化模型的建立

记针对配送中心的可动用车辆集为F={f|f=1,2,…,n},其中 f表示车号。

tf为针对f的选择变量(决策变量),tf∈{0,1},f=1,2,…,n;uf为第f辆车的载重量(吨位)。

G表示配送需求总量。

l表示路径号,L表示路径序列集合,l∈L。

xlf表示f号车行驶l号路径时的装载量,dlf表示f号车行驶l号路径时的距离。

如果xlf的装载量存在拼货情况(存在对几个配送地同时配送的情况),则l的取值就同时影响到dlf的取值,因此需要对l路线进行优化。本研究通过下述2个步骤解决了l路线优化问题:

1)先针对配送路径库,生成配送路径子网,形成路径序列集合L。例如,0—6表示从配送中心O至配送地6的路径,那么d0—6f表示车辆f从配送中心O行驶至配送地6的最短距离。

2)如果存在拼货的情况,采用就近插入法的原则,将需要拼货的配送地进行连接,再进行路线的优化。例如,装载车辆 f不仅装载了从配送中心O到配送地6的货,而且也拼装了配送地5的货。这时针对f号车的行驶路线也优化成最短的0—5—6或0—6—5路线。以下同理进行。

上述逐级递阶路线优化是遵循货物装载与路线优化同步的方式进行的。于是,用整数规划描述的车辆调度优化模型VSOP为:

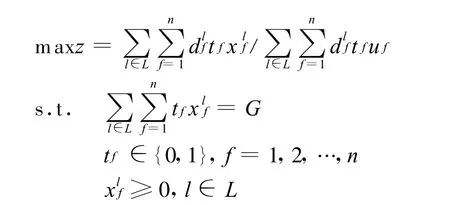
显然,这是一个非线性混合型规划,为求解这类规划问题,本研究采用了简化的方法。简化的思路如下:由于VSOP是一个兼具线路(包括距离)与车辆约束的车辆调度优化模型,故可以将线路的优化放在求解过程中(具体的求解步骤中)进行。因此,可以将VSOP模型简化为单纯的车辆调运优化模型,即简化为下述的调运优化模型P来求解[7]:

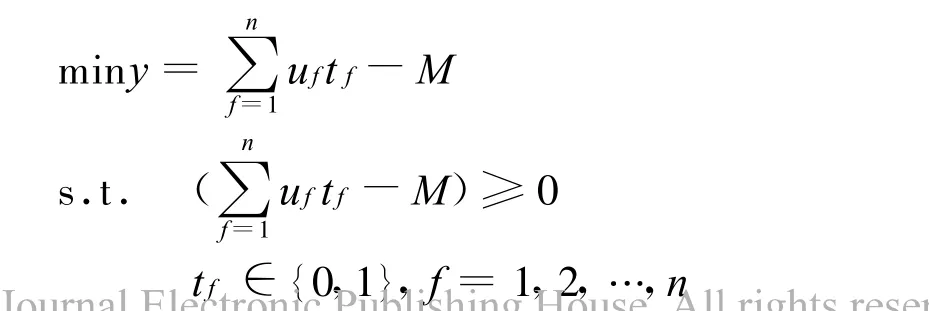
求解模型P的算法如下:

1)按敏捷调运知识准则中第一至第四级优先准则对配送单表(需求清单表)进行排序并分解。

2)利用模型P对分解清单进行求解。利用就近插入法原则对配送路线进行优化,得到车辆的配载清单,同时刷新可动用车辆集F。

3)重复1)、2)中的操作。

4)求得所有的装载方案,并计算出装载率。

2.2 模型的求解结果与分析

遵循上述模型P的求解算法,得到求解之后的调运方案如表4所示。

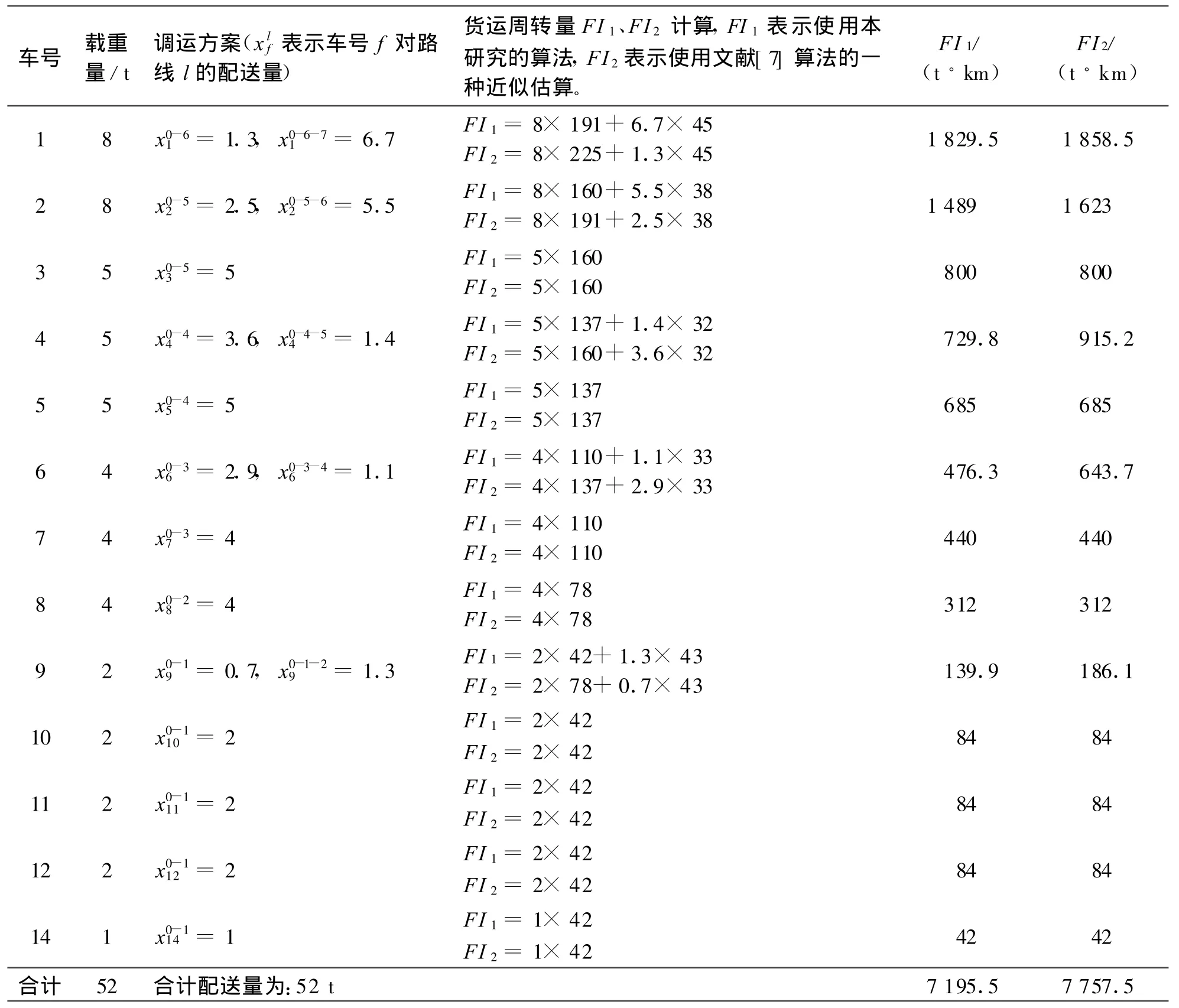
表4 模型P求解后的调运方案Table 4 Scheduling planning of solving model P

采用本算法的调运结果为:装载率为100%,货运周转量为7 195.5 t◦km,而使用文献[7]得出货运周转量为7 757.5 t◦km。其中13号、15号、16号车没有被调运。由此可见,本研究算法有较强的优越性,与文献[7]中的算法相比较,货运周转量减少了562 t◦km。

2.3 装载率的讨论与分析

虽然本例中的装载率为100%,但只是针对一批货物集中调运的情况,还并不具备代表性。为了针对每一次不同的集中调运情况,以及更精确地估算出各次调运后的装载率。本研究根据上述例子中的车辆详细信息对调运优化模型P的装载率进行了测量,测量的步长为0.1 t,通过使用Delphi编写相应的程序,得到如图1所示的测量结果。

在图1中,在敏捷调运知识准则支撑下,通过对调运优化模型P的装载率进行测量后发现,其装载率区间结果非常好,当配送任务装载量在20 t(见图1中的横坐标200单位)以上时,装载率基本上保持在95%～100%之间。

本研究中使用的简化模型P与文献[7]使用的模型P相比,并没有多出动车辆,只是两个模型处理不同的数据而已。本研究中车辆数据的选取,特别是车辆吨位的设计是参考斐波拉契数列来配备每辆车的吨位。实践也证明,企业在配备可供调运车辆时,应该考虑到不同吨位车辆的合理配备,以参考斐波拉契数列(1,1,2,3,5,8,13,21,…)来配备每辆车的吨位,车辆数量尽量服从正态分布,这样做是非常有利于节约运输成本的。

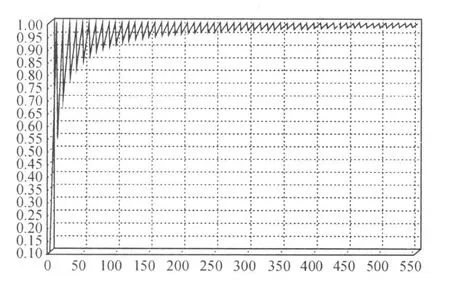
图1 车辆装载率估算界面Fig.1 Interface of measuring on vehicle loading rate

3 结 语

本研究吸收了文献[6]和文献[7]的精髓,根据某实际问题的简化数据,构造并完善了适应于实际问题的敏捷调运知识准则,是非常有应用价值的。

在敏捷调运知识准则的支持下,提出了车辆调运优化模型VSOP,它是一个非线性规划模型,通过将它转换为一个较为通用的模型P进行求解,所得装载率非常高。而且,其结果与同类算法相比,货运周转量也相对较低,行驶吨公里下降了562 t◦km,从而有效降低了物流调运成本。

[1] TUZUN D,BURKEL I.A two-phase tabu search approach to the location routing problem[J].European Journal of Operational Research,1999,116(1):87-99.

[2] BAITA F,PESENTI R,UKOVIC W,et al.A comparison of different solution approaches to the vehicle scheduling problem in a practical case[J].Computers&Operations Research,2000,27(13):1249-1269.

[3] CAMPBELL A M,SAVELSBERGH M.Efficient insertion heuristics for vehicle routing and scheduling problems[J].Transportation Science,2004,38(3):369-378.

[4] 李军,郭耀煌.物流配送车辆优化调度理论与方法[M].北京:中国物资出版社,2001.

[5] 王富忠,沈祖志.现代物流敏捷调运的运作体系与调运方式研究[J].浙江科技学院学报,2008,20(3):200-204.

[6] WANG F Z,SHEN Z Z,YU F M.Research of realizing logistics scheduling agility on the basis of semi-hierarchical control mechanism[C]//Proceedings of 2006 International Conference on Machine Learning and Cybernetics.Dalian,China:IEEE,2006:770-774.

[7] 王富忠,郭俊辉.物流敏捷调运实现的研究[J].浙江科技学院学报,2009,21(1):40-44.