一道值得商榷的高考题

葛 洲

(南京外国语学校,江苏南京 210008)

2010年海南高考物理试题中第5题是一道值得商榷的试题.原题如下:

如图1,水平地面上有一楔形物块a,其斜面上有一小物块b,b与平行于斜面的细绳的一端相连,细绳的另一端固定在斜面上.a与b之间光滑,a和b以共同速度在地面轨道的光滑段向左运动.当它们刚运行至轨道的粗糙段时

(A)绳的张力减小,b对a的正压力减小.

(B)绳的张力增加,斜面对b的支持力增加.

(C)绳的张力减小,地面对a的支持力增加.

(D)绳的张力增加.地面对a的支持力减小.

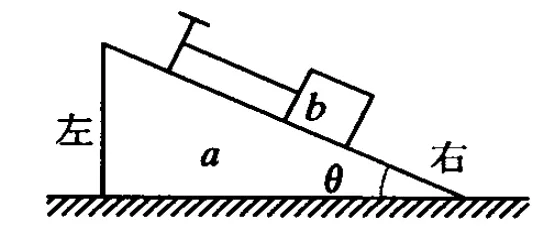
图1

试题给出答案为(C),笔者认为(C)选项仅仅是一个可能的答案,而不是一定的情况,因此本题表述有问题.

分析:设a质量为M,b质量为m,地面对 a的支持力为N1,绳上张力为 T,斜面对 b的支持力为N2.

(1)在光滑段运动时,以 a、b整体为研究对象,它们共同做匀速运动可得N1=(M+m)g.以b为研究对象可得T=mgsinθ,N2=mgcosθ.

(2)当它们运动到粗糙段时,设 a与地面间的动摩擦因数为μ.

临界状态为绳子仍然是直的,但张力刚好减为零.以a、b整体为研究对象,a、b共同加速度a=μg,以 b为研究对象a=gtanθ,此时 μ=tanθ即为临界条件.

①μ≤tanθ时,a、b一起做减速运动,加速度为 a=μg,方向水平向右.

以a、b整体为研究对象,由竖直方向受力平衡得 N1=(M+m)g.

图2

以b为研究对象,把加速度 a沿斜面方向和垂直于斜面方向分解,如图2.应用牛顿第二定律,沿斜面方向有

T=mgsinθ-max=mgsinθμmgcosθ,

垂直于斜面方向有

N2=mgcosθ+may=mgcosθ+μmgsinθ.

与光滑段时的T,N1,N2表达式对比得,此时,T减小,N1保持不变,N2增加.

②μ＞tanθ时,a将相对于b向上滑动,b物体有竖直向上的加速度分量,处于超重状态,所以 N1＞(M+m)g,定量分析可计算出 N1的大小,过程如下:

以a物体为参照物,设a物体加速度为a,b相对于a的加速度为a相,方向沿斜面向上,对 b受力分析,如图3,其中 ma为非惯性力,应用牛顿第二定律得

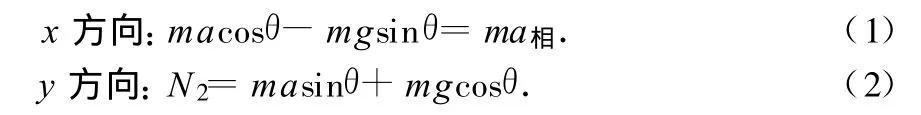
图3

图4

对 a受力分析,如图4,应用牛顿第二定律得

其中 N2=N2′.

由(2)～(4)式可解得

所以 μ＞tanθ时,N1＞(M+m)g,与光滑段 N1表达式对比得:N1增加;把(2)式与光滑段 N2表达式对比得:N2增加;此时 T=0,显然 T减小.由(1)～(4)式可解得

μcosθ-sinθ＞0,即μ＞tanθ,反映了μ=tanθ即为临界状态.

综上所述,所有选项都不正确.给出的标准答案为(C),其实(C)选项是可能出现的情形之一,而不是一定会出现的结果.当μ≤tanθ时,地面对物体a的支持力保持不变.