高中物理习题教学中物理模型方法的教学策略

张惠钰

(江苏省苏州第十中学,江苏苏州 215006)

物理习题教学是学生体会和实践物理模型方法的重要场所,在习题教学中往往通过指导学生运用物理模型方法分析和解答实际的物理问题,在解决问题中培养与训练学生的物理模型思维.从物理模型方法的特点和认知心理学角度,物理模型方法在习题教学中的教学策略可以分为3个阶段:第1阶段是陈述性知识教育阶段,即模型方法的狭义应用,这一阶段物理模型方法教学的任务是将过程模型所遵循的所有物理规律建构数学模型;第2阶段是可以相对自动化的程序性知识教学,即用物理模型方法解决一些简单的问题,这一阶段物理模型方法教学的任务是将问题情景建构成过程模型、将过程模型所遵循的所有物理规律建构数学模型;第3阶段为策略性知识,即在学生头脑中形成模型方法认知策略,让学生体验模型方法应用的条件,使模型策略学习达到反省认识的水平,有效地向新情境迁移,让学生在生活中有意识地运用模型方法去解决实际问题,这一阶段物理模型方法教学的任务是将具体问题中的实体建构成对象模型、将问题情景建构成过程模型、将过程模型所遵循的所有物理规律建构数学模型.

1 习题教学第1阶段

在习题教学第1阶段主要培养学生将过程模型所遵循的所有规律建构数学模型的能力,这一阶段在教学中所选习题的研究对象本身应该是已经简化、纯化的对象模型,问题情境也是比较明显的过程模型.在教学中我们可以选择变式拓展、层层深入的问题链,通过有意义的接受学习来组织教学,教学过程可以是“学习—模仿—迁移”,通过这些习题不但培养了学生识别模型的能力,而且还培养了学生把过程模型转化为数学模型的能力.

案例1:变式拓展训练——捕捉带电粒子在复合场中的舞步

如图1,空间存在水平方向的匀强电场和匀强磁场,强度分别为E=10N/C,B=1 T,如图1所示.有一质量为m=2.0×10-6kg,带正电 q=2.0×10-6C的微粒,在此平面内做匀速直线运动,其速度的大小为________,方向为________.(20 m/s,斜向右上方,与水平方向成60°角)

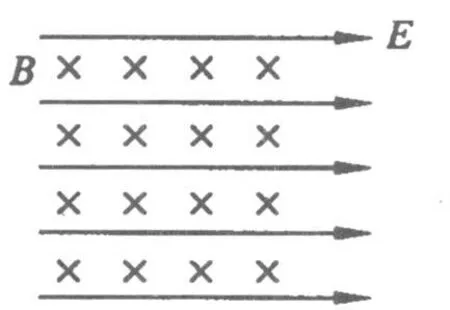
图1

总结:在不同的情景下,体验匀速直线运动的动力学规律:合外力为零,利用假设的方法来验证自己的猜想.之后配拓展1、2来进一步理解.

拓展1:如果是同样质量和电荷量的负电荷在此平面做匀速直线运动,则速度的大小和方向如何?(20 m/s,斜向左上方,与水平方向成60°角)

拓展2:如果该微粒的质量很小,重力可忽略不计,则微粒该如何进入这个复合场才能匀速通过该区域,且穿过的速度为多大?(从下往上垂直于电场射入,10m/s)

拓展3:如果在某一瞬间突然撤去磁场,则它相对于撤去时的位置上升的最大高度为多少?并求最高处的速度.(15 m,40 m/s)

总结:在不同的情景下,体验解决匀变速曲线运动的一般方法,体会运用等效的思想来解决问题.

引入:要想主动控制带电粒子的运动,我们如何设计它所处的环境.

拓展4:要使该带电微粒在该区域做速率为v=20 m/s的匀速圆周运动,将如何改变匀强电场的方向?E为多大?并请求出它的旋转方向与转动半径.(10 N/C,竖直向上,逆时针转动,20 m)

借鉴:可以从以下一个更为复杂的通过场力控制的运动来体会带电粒子的可控运动,体会带电粒子在复合场中的“舞步”,进一步体会解决多过程运动的方法.

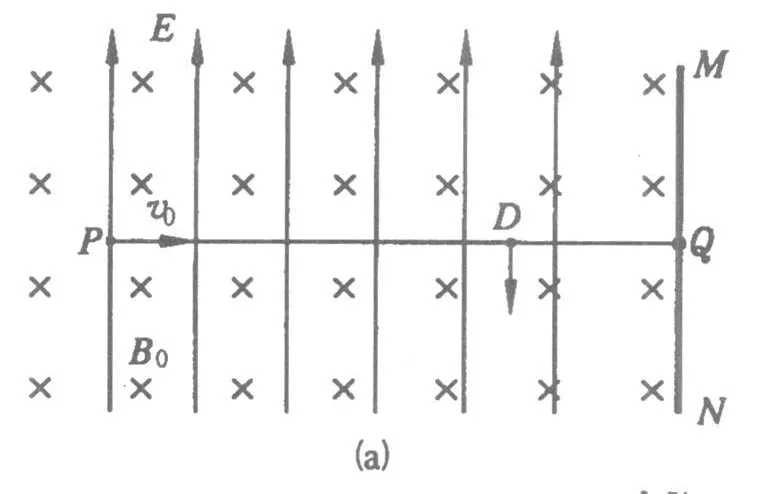
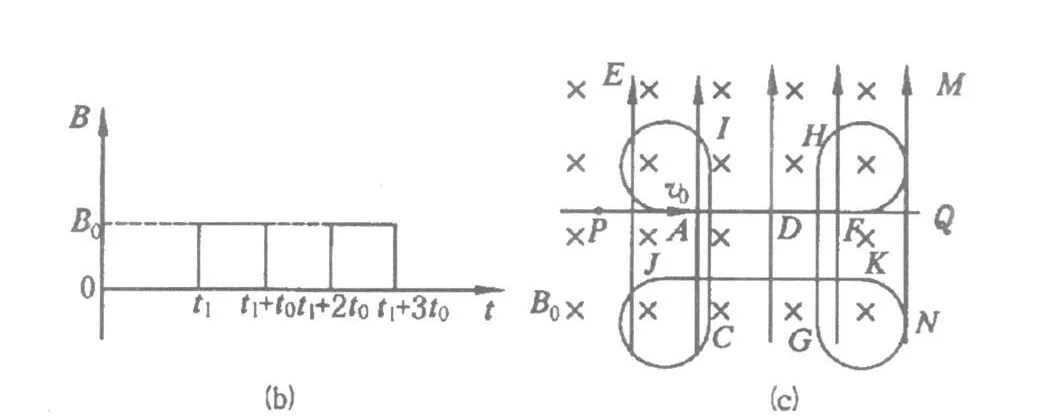
图2

拓展5:如图2(a),与纸面垂直的竖直面 MN的左侧空间存在竖直向上的匀强电场,上下及左侧无界,一个质量为m,电荷量为q的可视为质点的带正电的小球,在 t=0时以大小为v0的水平速度匀速向右通过电场中的一点P,当t=t1时刻在电场中加随时间周期性变化的磁场如图2(b),使得小球能竖直向下通过D点,D为电场中小球初速度方向上的一点,PD间距离为L,D到竖直面MN的距离,设B垂直纸面向里为正.

求:(1)如果B0为已知量,试推出满足条件时t1的表达式.

(2)若小球能始终在电场所在空间做周期性运动,则当小球运动的周期最大时,求出磁感应强度B0及运动的最大周期T的大小,并画出小球运动一个周期的轨迹.

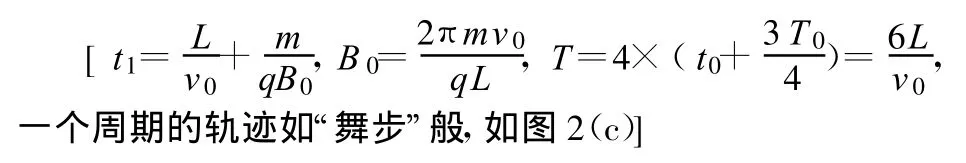
2 习题教学第2阶段

赵凯华教授认为:在教学中,同一问题,既可以把原始的物理问题给学生;也可以由教师把物理问题分解或抽象成一定的数学模型后再提交给学生,习惯于解后一类问题的学生,在遇到前一类问题时,往往会不知所措.

通过第1阶段的变式训练,学生具备了数学建模能力,但如果在教学中只一味地进行变式训练,则在遇到实际问题时,会一筹莫展,因此,习题教学第2阶段主要培养学生初步应用模型方法处理一些简单的实际问题.在习题教学第2阶段教学中所选习题的对象模型应该是比较清晰的,问题情境可与实际生活、生产相联系,或者以估算题的形式出现,通过这些简单的实际问题让学生学会如何把问题情境转化为过程模型,再利用数学模型解决问题.通过这类实际问题的模型方法的训练,使学生体会到模型方法的价值与作用,并从中得到有益的启示.

案例2:(2009年宁夏卷)——提供冰壶运动的视频引导学生建模

冰壶比赛是在水平冰面上进行的体育项目,比赛场地示意图如图3.比赛时,运动员从起滑架处推着冰壶出发,在投掷线AB处放手让冰壶以一定的速度滑出,使冰壶的停止位置尽量靠近圆心 O.为使冰壶滑行得更远,运动员可以用毛刷擦冰壶运行前方的冰面,使冰壶与冰面间的动摩擦因数减小.设冰壶与冰面间的动摩擦因数为μ1=0.008,用毛刷擦冰面后动摩擦因数减少至 μ2=0.004.在某次比赛中,运动员使冰壶C在投掷线中点处以2 m/s的速度沿虚线滑出.为使冰壶C能够沿虚线恰好到达圆心O点,运动员用毛刷擦冰面的长度应为多少?(g取10 m/s2)

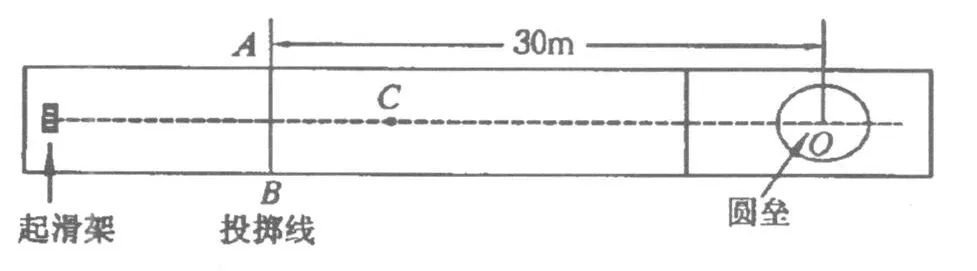
图3

物理模型方法过程:

作为冰壶运动的对象模型比较清晰,这里的关键是将问题情景建构成过程模型.

问题情景建构成过程模型:

可以利用网络视频,如http://v.youku.com/v_show/id_XNzcyNDc3NzI=.html帮助学生建立物理模型,在习题教学中通过实际的情境让学生抽象出问题的情境可以分解为不同加速度的两个匀减速直线运动的阶段.

过程模型所遵循的所有物理规律建构数学模型:

设冰壶在未被毛刷擦过的冰面上滑行的距离为s1,所受摩擦力的大小为 f1=μ1mg;在被毛刷擦过的冰面上滑行的距离为 s2,所受摩擦力的大小为 f2=μ2mg.则有

式中s为投掷线到圆心O的距离.由功能关系

由(1)、(2)式解得

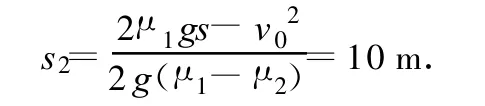
3 习题教学第3阶段

习题教学第3阶段主要培养学生在遇到实际问题时运用物理模型方法解决问题的能力,这一阶段所选的习题是以原始的物理问题、分析、辨析等方式呈现,所选习题原始问题的对象模型并不清晰,处理原始问题时还需要将原始情境抽象为理想过程模型,再把过程模型转化为数学模型.

案例3:如图4(a)所示,底面半径为 r,高为 h的圆锥形陀螺在光滑水平桌面上快速绕轴旋转,同时以速度v0向右运动,若陀螺的转动轴在全部时间内都保持竖直,则v0至少等于多少,才能使陀螺从桌面滑出后不会与桌边发生碰撞?

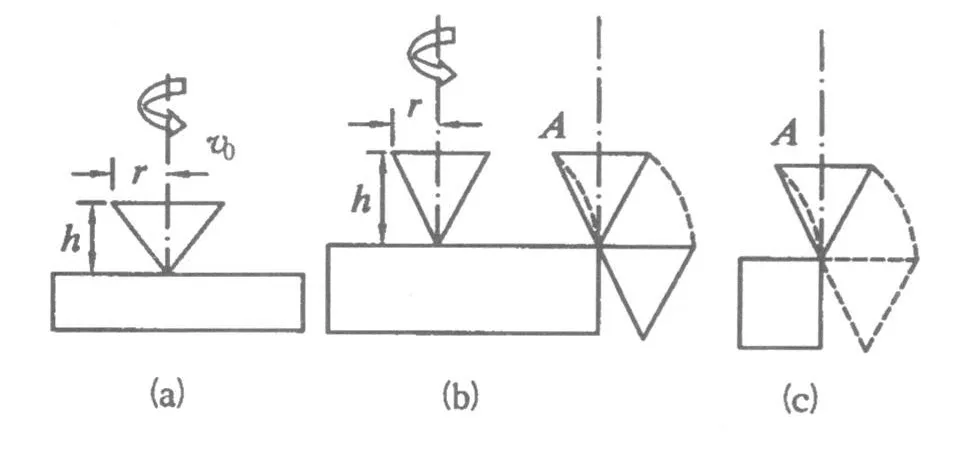
图4

物理模型方法过程:

具体问题中的实体建构成对象模型:陀螺运动时既有转动又有平动,但是陀螺的转动轴在全部时间内都保持竖直,且陀螺不会与桌面接触,因此将陀螺当作平动的物体研究,依照题意画出陀螺平动的草图如图4(b)所示 .陀螺不会与桌面接触,陀螺做平抛运动,取陀螺运动左上边缘 A点,A点的轨迹恰好经过桌边,故抽象出陀螺运动左上边缘 A点为对象模型,如图4(c)所示.

问题情景建构成过程模型:

陀螺从桌面滑出后不会与桌边发生碰撞,可以将复杂的陀螺运动抽象成为理想的质点A做平抛运动.

将过程模型所遵循的所有物理规律建构数学模型:

通过这3个阶段的习题训练,可以帮助学生理解、体会这一模型思维方法,特别是最后阶段的练习,能使学生意识到模型方法的意义和作用,并能使学生在生活中遇到问题时能有意识地应用这种思维方式去处理实际问题.如汽车司机在行驶过程中突然发现前方有险情,为了避开危险,司机应当采取紧急刹车还是紧急转弯的措施?处理这一问题时首先根据情境把实体模型抽象为对象模型,再将原始情境抽象为紧急刹车时的匀变速直线运动和紧急转弯时的匀速圆周运动两种理想过程模型,最后根据过程模型转化为数学模型.学生通过解决问题的过程中直接地感受到学习物理模型方法的意义,掌握物理模型的方法.