小组合作是深度学习的有效途径

陆天明

(南京师范大学附属中学江宁分校,江苏南京 211102)

我校一直开设“个性化辅导”课程,学校规定这类课是只让学习上有困难的学生参加,由于这种辅导方式会对成绩不太好的学生造成心理压力,所以我采用变通的办法,不对学生按成绩分组,而是采用自然分组的办法,每次上“个性化辅导”课时,留下班上的一个自然组,让这个自然组中成绩较好的同学但任“主讲”,搞成“学术沙龙”的形式,活动内容主要来源于课堂上和作业中的问题.我不参与讨论,只是旁听.由于小组人数不多,而且学生之间在交流时也没有太多的心理障碍,所以会畅所欲言,对问题的讨论有时会非常深入,产生让人意想不到的学习效果.这里说的就是高三一次“个性化辅导”课上所发生的事,主持本次“沙龙”的是班上一名参加竞赛的同学.

主持人:“本次“沙龙”要讨论这几天物理学习中遇到的一些问题,欢迎各位提出自己的疑问,大家一起研讨”,要发言的同学请先举手,有同学发言时其他学生不要打断!

这时陈同学要求发言,陈同学物理水平不高,在开学的期初考试中物理只得了2分,选择题竟然一题也不对,陈同学在黑板上就下面的题目向各位同学作了表述:

如图1所示,用轻绳将小球挂在某固定点,现在将轻绳水平拉直,然后由静止开始释放小球,考虑小球由静止开始运动到最低位置的过程

(A)小球在水平方向的速度逐渐增大.

(B)小球在竖直方向的速度逐渐增大.

(C)小球在到达最低位置时线速度最大.

(D)小球在到达最低位置时绳中的拉力等于小球的重力.

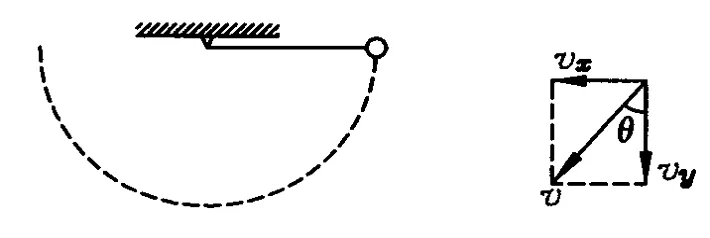
图1

他说:“老师在课堂上对(A)、(C)、(D)3个选项的解释没有什么问题,但对于(B)项的解释.

“陆教师说,因为小球初速度为零,末速度的方向是水平的,这时在竖直方向的速度为零,而过程中小球在竖直方向上的速度是不为零的,所以小球在竖直方向上的速度有一个先增大再减小的过程,所以(B)项是错误的.”.“陆教师对小球在竖直方向上的运动所作的分析觉得有点玄,我非常想知道小球在竖直方向上到底是如何运动的.”

主持人:“这个可能比较复杂,根据我的经验,用微元法可能是比较好的思路,在绳与水平方向成θ角处取一微元进行分析”如图2,接着他在黑板上进行了如下运算:

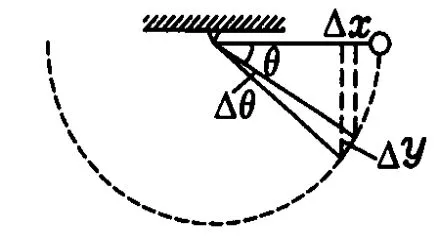
图2

这样就得到了速度的表达式,正在主持人得意时,宋同学迫不及待地站了起来.

宋同学:“Δy=Rcosθ·sinΔθ是可以直接从图上的几何关系中看出来的,没有必要这么复杂.”

宋同学就在图3的作了标注,获得同学们的又一阵掌声.王主持人显得有点尴尬.这时闫同学又站了起来.

图3

闫同学:vy=ω Rcosθ中的ω和θ都是在增大的,函数的单调性没有办法看出来.

许同学:这很简单,只要把 ω换成θ的函数就行了,用v=ω R和机械能守恒定律就行了.

陈同学:“利用 v=ω R那不就是vy=vcosθ,这不是速度的分解吗?为什么要用“微元法”这种让人难以琢磨的办法呢?”

王主持人自我解嘲说:“我确实是用导弹打了蚊子,但同学们总可以欣赏一下我的这种高级的解法吧”.这时许同学主动上黑板求 vy的表达式.经过一番并不复杂的计算得到下式:

对于这个函数的单调性问题,许同学一筹莫展.这时王主持人又来了劲,说道:“这个可以用微积分来处理,对这式子求导,并令这个导数为零,解出……”.陈同学打断王主持的话说:“请你不要再放导弹了,这个我们不懂,你有本事用我们学过的数学知识讨论”.这时又有一位姓张的同学上黑板做了如下运算:

张同学如此巧妙的演算迎来一阵热烈的掌声.突然高同学很激动地站了起来说:“我与各位的思路截然不同,我是从受力的角度来加以分析的.”王主持人示意高同学来到讲台前,只见高同学在黑板上画了小球的受力图4,令人惊讶的是,他竟然不是按常规把重力进行分解,而是把拉力进行了分解.

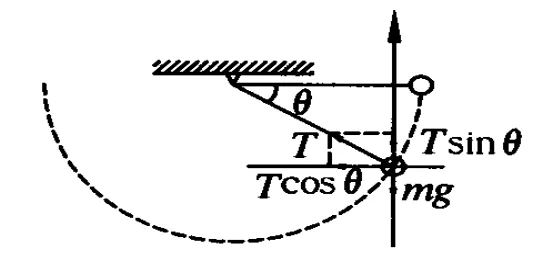
图4

高同学:“我认为,圆周运动不一定非要紧盯着向心力和向心加速度,圆周运动也可以用正交分解法,分为 x方向上的运动和y方向上的运动,圆周运动是这两个方向上运动的叠加.x、y方向上的的两个运动与圆周运动是等效的.现在我们只考虑竖直方向上的运动,显然,绳子开始时拉力为零,在最低点时由于超重应大于重力,而且不难看出整个过程中拉力是单调递增的,在某个位置一定有 Tsinθ=mg,这是一个临界点,在此之前速度是增大的,在此之后速度是减少的.”

主持人:“这种对圆周运动的处理办法我倒是没有见过,确实令人耳目一新,但用这种方法能不能定量算一下这个临界点的位置呢?”

高同学:“我还没试过.”

于是主持人要求大家在下面想办法运算一下.不一会,高同学兴奋地说算出来了,于是上黑板写下了他的算式:

在这节辅导课上我只是观众,从头至尾没有说一句话,然而感触很深.学生们所研究的只是一道很平常的问题,可是经过小组合作学习,竞然会引出如此深入的讨论,不仅综合运用了力学中几乎所有的主干知识:受力分析、运动分析、运动的分解与合成、牛顿定律、机械能守恒定律等等,而且使用到了多种思维方法:微元法、临界分析法、极值法、等效法、数学法等.此外,在这节课上,所有的学生都参与了发言和讨论,气氛愉快,学生关系显得非常融洽,这节课所达到的教学效果是任何一节普通课无法比拟的.

美国著名心理学家布卢姆根据人的认知过程从简单到复杂,由具体到抽象这一规律来作为教育目标分类理论,在认知学习领域中把教学目标分成6大层次,从低级到高级依次为:(1)识记:主要指记忆知识,对学过的知识和有关材料能识别和再现.(2)理解:主要指对知识的掌握,能抓住事物的实质,把握材料的意义和中心思想.(3)应用:指把所学的知识应用于新情境.(4)分析:分析指能将知识进行分解,找出组成的要素,并分析其相互关系及组成原理.(5)综合:指把各个元素或部分组成新的整体.(6)评价:根据一定的标准对事物给予价值的判断.浅层学习(surface learning)的认知水平停留在第一层和第二层,而深度学习(deep learning)则对应着后面的4个层次.深度学习的起点是浅层学习深度,学习不只涉及记忆,更注重在理解基础上对知识的应用,并能够将己有的知识迁移到新的情境中,深度学习还要求学习者有一种积极的态度.

深度学习理论要求我们所采用的相应的教学设计策略应该是:(1)基于问题的学习,即针对课堂教学的重点和难点,提出有思维价值的问题来引发学生的深度学习,并为学生创造更多的独立思考和讨论的机会.(2)创设任务驱动式学习,任务驱动式学习也称为基于任务的学习,教师结合某一知识内容提出一个主题或任务让学生自己去探究.(3)小组合作学习,即以学习小组为组织教学的手段,通过小组成员之间的合作,发挥群体的积极功能,提高小组中各个成员的学习动力和能力,完成特定的教学任务.小组合作学习不仅改变了在传统集体教学中师生的单维交流,而且改变了由于教师垄断了整个课堂的信息源而使学生处于十分被动的局面,使学生的主动性、创造性因此得以充分的发挥.

有一句非洲格言:“如果你想走得快,那么你就一个人走;如果你想走得远,那么就一起走.”此话很有意思,充满哲理.小组合作学习中的小组是一个学习团队,小组内民主和谐的学习环境,轻松愉快的学习氛围,组员之间的思维碰撞和团结协作可以很自然地把问题讨论引向深入,小组学习是深度学习一个有效途径.

1 何玲,黎加厚.促进学生深度学习.计算机教与学,2005(5):29-30

2 叶晓芸,秦鉴.论浅层学习与深度学习.软件导刊,2006(2):19-21