对向心加速度物理意义的探讨
2011-05-18汤家合
汤家合
(南京师范大学附属扬子中学,江苏南京 210048)
阅读本刊2010年第3期的文章《向心加速表示速度方向变化的快慢吗》(以下简称“向文”),很受启发,也引发了本人对相关问题的进一步思考.
“向文”给出了“物体的角速度是表示物体做圆周运动时速度方向变化快慢的物理量,向心加速度不能表示物体做圆周运动的速度方向变化的快慢”的观点,但对向心加速的物理意义并未论及.本文想结合物理学史的有关知识和本人的一些思考,给出向心加速的物理意义,供读者评鉴.
公元1666年,牛顿为了说明天体间的引力和地球上的物体所受的重力可能是同一种力而对此问题有所论述,下面就借此思想对该问题进行论证.
如图1所示,设质点在大小不变的向心力作用下做匀速圆周运动,质点开始位于圆周上的 A点,速率为 v,经过一段时间 t后,到达 B点.根据运动的合成与分解的法则,实际的“圆周运动可以看作是沿
切线方向的匀速直线运动与沿法线向心方向的匀加速直线运动的合成.故物体的实际位移AB可以看作是沿切线方向的位移AC与沿法线方向的位移CB的矢量和.


图1
由以上推导可以看出,物体做匀速圆周运动的向心加速度an就是瞬时法线方向匀加速直线运动的加速度a,它表示的是物体沿法线“落向圆心”运动时速度大小的变化快慢,是向心力作用的结果,即因此,向心加速度 an与直线运动中的加速度没有本质的区别,它们都是描述速度大小随时间变化快慢的物理量.在匀速圆周运动中,线速度的大小不随时间变,而方向时刻在变,其实是物体沿圆周切向的惯性运动和物体沿半径方向“落向圆心”的匀加速直线运动合成的结果.
一脉相承,中学物理所学的平抛运动和斜抛运动都可以进行类似的处理:如图2,平抛运动可以看成是水平方向的匀速直线运动和竖直方向的自由落体运动的合成;如图3,斜上抛运动可以看成是沿初速度方向的匀速直线运动和竖直方向的自由落体运动的合成.而这两例中物体的加速度和圆周运动中的向心加速度都没有本质的区别,均表示了速度大小的变化快慢.
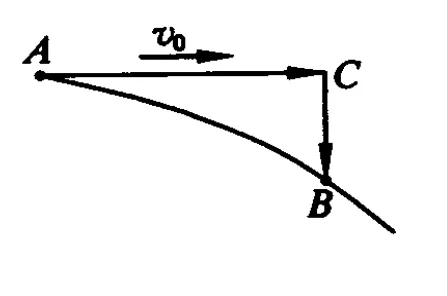
图2
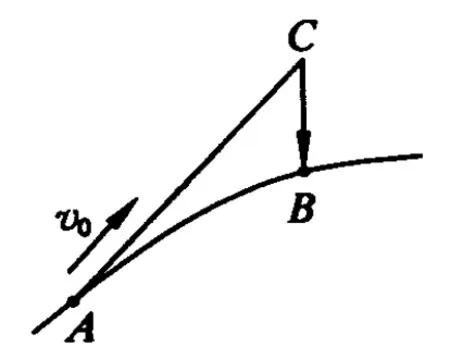
图3
下面再进一步讨论两个与此相关的问题.
问题1:向心加速度与角速度
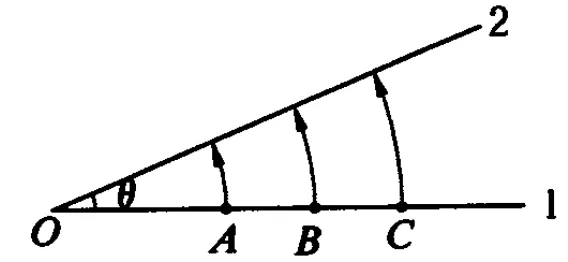
图4
如图4所示,位于同一杆上的质点 A、B、C具有相同的角速度,当杆从位置1匀速转动到位置2时,3个质点速度方向的改变相同,故速度方向改变的快慢也相同,但3个质点的向心加速度并不同.这说明向心加速度确实不是描述速度方向改变快慢的物理量,而角速度才是描述速度方向变化快慢的物理量.半径越大物体做圆周运动时所需的向心力也越大,故向心加速度越大,这说明物体沿半径“落向圆心”运动速度的大小改变越快,并不说明速度的方向改变越快.
其实,“向心加速度表示圆周运动物体速度方向变化的快慢”这一观点在正规的教科书中是找不到的(如高中物理、普通物理、理论物理等教材),只是在各种教辅资料中广为流传,故在中学阶段对向心加速度概念的教学产生了负面影响.
问题2:变速圆周运动中的加速度
如图5所示,设物体沿圆周做变速运动由 A点运动到B点,速度由 vA变为vB,所用时间为Δt.若在矢量 vB上截取长度等于vA的一段后得到矢量Δv2,它反映了速度大小的变化;而图中的Δv1则反映了由速度的方向变化而引起的速度改变.易知Δv=Δv1+Δv2,其中Δv1为向心力所致,Δv2为物体所受合力沿切向的分力所致.
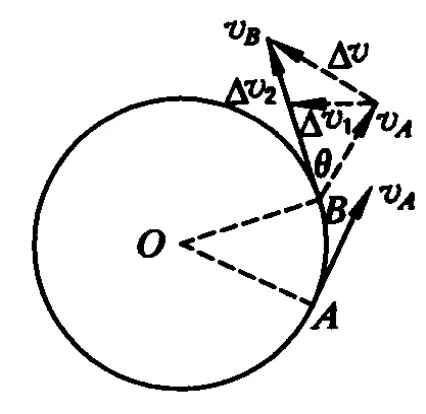
图5
1 潘永祥,王锦艺.物理学简史.武汉:湖北教育出版社,1990.234
