基于线性回归的无线传感器网络加权质心定位算法
2011-05-15姚维照
胡 彧,姚维照
(太原理工大学测控技术研究所,太原030024)
在传感器网络中,位置信息对传感器网络的监测活动至关重要,传感器网络节点所采集到的数据必须结合其在测量坐标系内的位置信息才有意义。对此,传感器节点必须首先知道自身的地理位置信息,这是进一步采取措施和做出决策的基础。因此采用一定的机制与算法实现无线传感器网络的自身定位是很有必要的[1]。
笔者主要研究不基于测距的粗精度质心定位算法[2-3](Centroid Localization Algorithm,CLA)。CLA算法简单易于实现,计算速度快,平等地对待各个信标节点,但定位误差大,对信标节点的密度依赖性强。为了降低CLA算法的定位误差以及对信标节点较强的依赖性,本文对CLA算法进行多跳加权、误差扩大、线性回归校正及校正位置修正改进,提出了一种基于线性回归的加权质心定位算法(Liner Weighted Centroid Localization Algorithm,LWCLA)。改进算法降低了网络的平均定位误差,提高了节点定位比率,算法定位性能更加优越。
1 加权质心定位算法
1.1 基于跳数的加权质心定位算法
对CLA算法中的每个信标节点进行加权因子约束,分别体现它们对未知节点估计位置决定权的大小,就形成了加权质心定位算法(Weighted Centroid Localization Algorithm,WCLA)。其表达式通常如式(1),(2)的第一步[4]所示。目前WCLA算法有很多改进方案,基本上都是在测距模型的基础上改进权值因子[5,6]。本文的加权改进方案则基于测距无关模型,通过未知节点与信标节点之间的跳数关系来体现信标节点对未知节点坐标决定权的大小,如下所示:
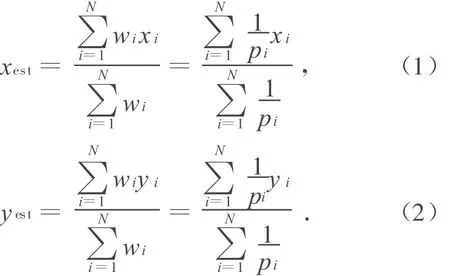
式中:N为信标节点数目;wi为信标节点i的权值因子;p i为信标节点i与未知节点之间的跳数。
网络中的每个未知节点都可以根据自己与信标节点之间的跳数信息利用WCLA算法计算自身的估计位置,所以无论网络中信标节点分布多少,网络中的所有未知节点都可以实现定位,从而使定位比率提高至接近1。图1第一列的三组图形是基于跳数信息的WCLA算法定位效果图,从图中可以看出改进后的算法的定位误差依然很大,并且未知节点的估计位置都不同程度的偏向于信标节点中心(所有信标节点位置取均值),此现象为中心化效应[7]。此现象也在预料之中,因为对于小型的网络分布,节点的跳数信息差别不大,与节点的实际距离相差很大,所以基于跳数信息的WCLA算法在改进CLA算法的同时,也保留了CLA算法定位误差大的缺陷;而且在改进方案中由于所有的信标节点都参与节点位置的计算,因此基于跳数信息的WCLA算法出现了中心化的效应。
1.2 位置估计中心化
基于跳数信息的WCLA算法在降低误差方面的效果不是很明显。但基于它本身中心化的特点,本文在WCLA算法的基础上进行加强中心化的改进[8](Improved Weighted Centroid Localization Algorithm,IWCLA),将基于跳数WCLA算法的定位误差扩大化,使位置估计中心化的效果更加明显清晰,找到节点定位误差之间的内在关系。其中心化的思路为:当未知节点根据加权质心算法获得自身的估计位置后,将此位置记录为自己的初次估计位置;当所有节点的初次估计位置都记录完毕,未知节点再与其通信范围内的所有邻未知节点交换信息,获得其他未知节点的初次估计位置,并将自己以及所有邻未知节点的初次估计位置取平均值记录为自己的最终估计位置。IWCLA算法的二次计算通过未知节点周围的邻节点来计算自身位置,该种方式以加法的方式扩大了未知节点与信标节点跳数信息的影响。因此,相对于WCLA算法,网络中未知节点的估计位置更加偏向于信标节点的中心,中心化的效果将更加明显,误差的规律性也将更加显著。
通过公式(3)可以计算节点的定位精度[9],由公式(3)可以看出,节点的平均定位误差和定位精度成正比,平均定位误差越小,定位精度就越小,算法的定位性能也就越好。

式中:L为节点定位精度;LE为平均定位误差;R为节点通信半径;n est为网络中可获得位置的节点数目;N为信标节点数目;n为网络节点总数;(x,y)为节点实际位置,(xest,yest)为节点估计位置。
在MATLAB仿真平台上,一般设定115个传感器节点随机均匀地分布在100 m×100 m的正方形区域内,网络中的信标节点数目N=15,通信半径R=50 m。分别对WCLA算法和IWCLA算法进行仿真对比,如图1所示。
图1 中的仿真结果证实了理论分析的正确性。其中黑色的点代表可以通过二次计算的方式来增强基于跳数WCLA算法的中心化效应,使估计位置的分布更具有规律性。表1中记录的是两种算法的L值,可以看出,IWCLA算法的平均定位误差较大,相对WCLA算法,IWCLA算法的定位性能降低了30%左右。但 IWCLA算法的中心化效应非常显著。中心化效应增大误差的同时,误差的分布更具有规律性,可借此规律尽可能减小误差。
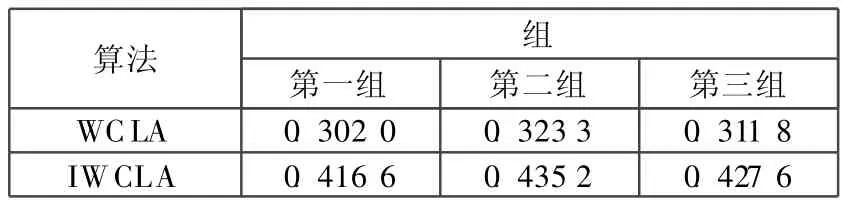
表1 WCLA算法与IWCLA算法L对比表
2 基于线性回归的加权质心定位算法
2.1 基于线性回归的加权质心定位算法
图1中,由IWCLA算法计算得到的估计位置都集中在信标节点的中心位置附近。将未知节点的估计位置与实际位置分别减去信标节点中心位置的坐标值后可得到如图2所示的关系分布图。从图2可看出,利用IWCLA算法定位未知节点的估计位置与实际位置存在一定的线性关系。利用线性回归的数学模型[10]确定该线性图像的关系系数,据此本文给出了位置校正公式如(4)—(6)所示,通过LWCLA算法获得位置的未知节点将按照此公式来校正自己的位置。可称此过程为去中心化过程,也可称为边缘化过程(未知节点的估计位置趋向于网络边缘)。
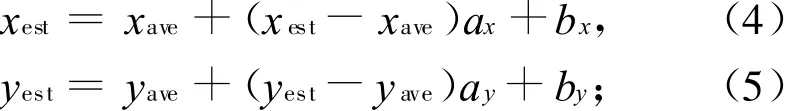
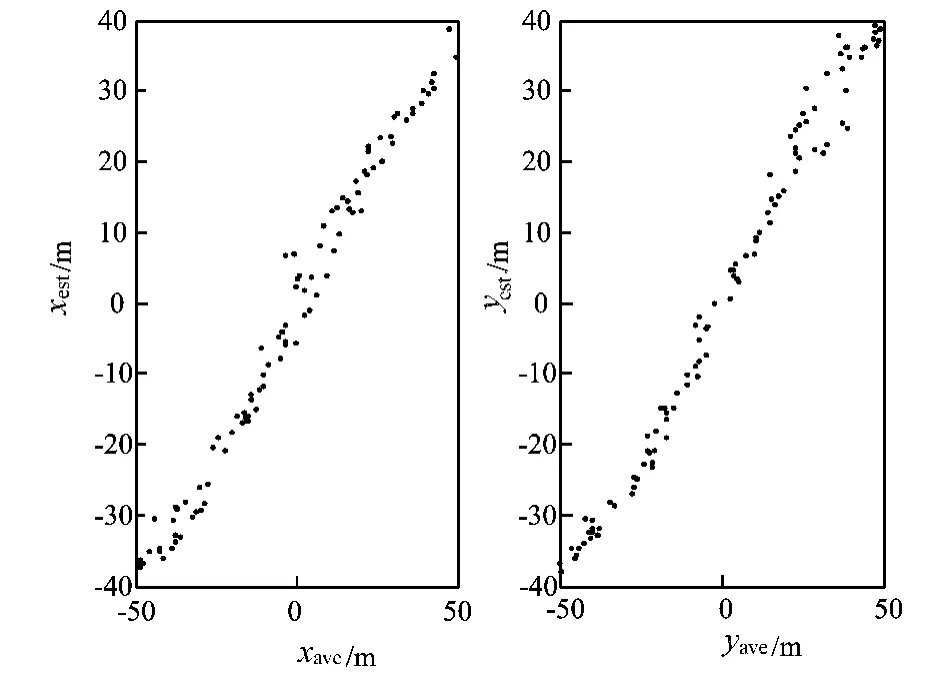
图2 未知节点的估计位置与实际位置的关系曲线图

由图3可以看出,网络中通讯半径R=15与节点总数n=115,经过1 000轮的仿真实验,校正系数ax,bx,ay,by的值波动不大。在本文中校正系数ax,bx,ay,by取1 000轮仿真实验的均值。还应考虑到由于网络节点的分布不同,校正系数ax,bx,ay,by的值如图3所示是波动的,并且图2所示的关系曲线表明节点的坐标关系并不呈严格的线性关系,针对所有的未知节点采用相同的校正系数,会出现去中心化太过,导致边缘化效应非常显著,使定位出现失真的情况。因此,为了合理估计待定位节点的位置,本文将边缘化、中心化及质心化(直接通过CLA算法计算得到的估计位置)三种位置估计按照本文所给出的公式(7),(8)进行修正。式中的修正系数a,b,c随着R与n数值的变化而发生变化,因此在利用此公式之前,应针对特定网络环境,在仿真实验上调节修正系数a,b,c,使定位误差达到最小。

式中:(xestc,yestc)为CLA算法估计位置坐标值;)为IWCLA算法估计位置坐标值;(x estl,y estl为LWCLA算法估计位置坐标值,a,b,c为修正系数,三者之和等于1。
2.2 仿真结果
IWCLA算法的定位流程可总结如下。
1)各个未知节点搜索自己范围内的邻节点,获得网络中所有信标节点的位置信息以及与它们的跳数关系。

图3 N=100,n=15,R=50时a x,bx,ay,by的关系图
2)各个未知节点根据收集到的信息,按照WCLA算法公式(1),(2)计算自身的估计位置。
3)各个未知节点与其通信范围内的邻未知节点交换信息,获得它们的估计位置,并将其自身以及所有邻未知节点的估计位置取平均值记录为自己的估计位置。
5)按照公式(4)—(6)及步骤4计算得到的校正系数校正自身的估计位置。
6)将步骤1,3,5所得的估计位置按照公式(7),(8)及由步骤4选择的修正系数对节点的位置最后进行修正。
7)按照公式(3)计算整个网络的定位精度,网络的定位误差越小,定位精度就越小,算法定位性能也就越好。
在2.2节设定的网络环境下,对WCLA算法、IWCLA算法及LWCLA算法进行仿真对比。

图4 三种算法定位精度对比图
从表2所记录的三种算法的L数值可以分析出,相对于WCLA算法,IWCLA算法的定位性能降低了31.46%,而 LWCLA算法的性能提高了62.58%。由此LWCLA算法在不基于距离信息的情况下使WCLA算法的定位误差下降了60%以上,改进效果非常明显。
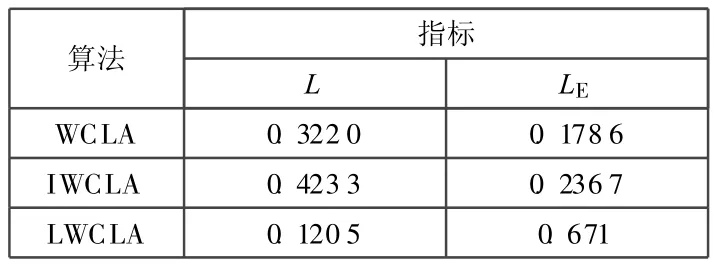
表2 三种算法定位精度对比表
图4代表三种算法的定位精度随着网络中信标节点的增多而降低的关系图。三种算法的平均定位误差都随着网络中信标节点数目的增多而不断下降,但 LWCLA算法的平均定位误差始终低于WCLA算法、IWCLA算法。取三种算法的平均定位精度LE作为对比指标,分析表2可以得出,与原始质心算法相比,LWCLA算法的L E下降了62.43%,也就意味着算法的平均定位误差下降了62.43%,定位性能提高了62.43%;并且LWCLA算法通过多跳加权及算法增强两方面的改进,在信标节点密度较低的情况下,使节点的定位比率提高至接近1。
3 结论
CLA算法简单易于实现,功耗低,对硬件设备要求不高,算法运行速度快,但其定位误差较大,仅能作为对未知节点实际位置的估计。本文提出的LWCLA算法在质心算法的基础上进行加权、中心化及利用线性回归的数学模型对节点位置进行校正,最后又对校正位置进行了修正。仿真结果表明,LWCLA算法简单易于实现,算法复杂度低,使CLA算法的定位误差降低了60%以上,在信标节点密度较低的情况下,还可使节点的定位比率提高至接近1,取得了良好的算法性能改善结果。
[1] 王福豹,史 龙,任丰源.无线传感器网络中的自身定位系统和算法[J].软件学报,2005,16(15):857-868.
[2] Nirupama Bulusu,John Heiemann,Deborah Estrin.GPS-less Low Cost Our-Door Locaization for Very Small Devices[J].IEEEPersonal Communications,2000,7(5):28-34.
[3] Deng B D,Huang G M,Zhang L.Improved centroid localization algorithm in WSNs[C]∥The 3rd International Conference on Intelligent System and Knowledge Engineering,2008:1260-1264.
[4] 陈维克,李文锋.基于RSSI的无线传感器网络加权质心定位算法[J].武汉理工大学学报,2006,30(2):265-268.
[5] 白进京,严新平,张存保.基于加权质心和DV-Hop混合算法WSN定位方法研究[J].计算机应用研究,2009,26(6):2248-2250.
[6] Gao Lipeng,Zhu Meidong,Yang Dan.Simulation and Implement of Weighted Centroid Localization Algorithm Based on Zig-Bee[J].Chinese Journal of Sensors and Aciuators,2010,23(1):149-152.
[7] 安恂,蒋挺,周正.一种用于无线传感器网络的质心定位算法[J].计算机工程与应用,2007,43(20):136-138.
[8] 李兆斌,魏占祯,徐风麟.无线传感器网络增强的质心定位算法及性能分析[J].传感技术学报,2009,22(4):563-566.
[9] Kerem Kucuk,Adnan Kavak.Scalable location estimation using smart antennas in wireless sensor networks[J].Ad Hoc Network,2010,8:889-903.
[10] 费业泰,陈晓才,秦 岚,陈林才.误差理论与数据处理[M].北京:机械工业出版社,2007:120-155.
