循环伏安法测定Ti/SnO2+Sb2O x/PbO2阳极的分形维数及电催化性能

梁镇海,李付合,宋秀丽,李双志

(太原理工大学化学化工学院,太原030024)

影响电极电催化性能的主要因素有电子因素和几何因素。电子因素主要与电极的组分和各组分的物理化学特性有关系,几何因素则直接与电极的表面形貌有关[1]。电化学反应是一种多相反应,多相催化反应的一个显著特征就是在整个反应过程中都存在反应界面,而界面的结构性质对反应过程有重要的影响。一般认为在析氧电位与析氢电位之间的阳极伏安电荷q*与电极电化学活性表面积成正比[2],而电化学活性表面积可用来反映电极的结构和电化学性能[3]。由Mandelbrot[4]建立起来的分形几何学为解决诸多粗糙表面的复杂问题提供了新的途径和思路,尤其对材料的表面结构与性能研究有着重要的理论和实际意义[5,6]。Pajkossy[7,8]采用扩散控制条件下的循环伏安法测定电流和时间的关系并计算了材料的分形维数,但是目前将分形维数应用于钛基氧化物电极电催化性能方面的研究还未见报道。因此,本文通过循环伏安曲线测定了Ti/SnO2+Sb2Ox/PbO2电极表面的分形维数,以期为钛基氧化物电极的开发和应用提供理论和实验依据。

1 实验部分

1.1 电极制备

用砂布对钛片进行打磨,将基体边缘磨圆以克服边缘效应。打磨后的钛片置于90℃、质量分数为40%的氢氧化钠溶液中浸泡2 h,然后用质量分数为10%草酸溶液煮沸酸蚀。当钛片表面呈均匀的灰白麻面时,取出,用蒸馏水洗净备用。

将SnCl4◦4H2O和SbCl3◦3H2O按一定比例配成盐酸-正丁醇涂液,均匀涂覆在预处理过的钛基体表面。110～120℃下干燥箱烘干10 min,之后在450℃下焙烧10 min,取出后自然冷却。然后按以上步骤反复操作20次,最后一次在550℃下烧结1 h,得 Ti/SnO2+SbO x电极。

用制备好的Ti/SnO2+SbO x电极做阳极,选取同等面积的钛板作阴极,电解质溶液组成为：0.1 mol/L HNO3,0.5 mol/L Pb(NO3)2,0.08 mol/L Cu(NO3)2◦3H 2O及40 mmol/L NaF添加剂。控制电流密度为20 mA/cm2,进行阳极电沉积3 h,即得Ti/SnO2+Sb2O x/PbO2电极。

1.2 电极性能测试

用Amray 1850型扫描电子显微镜观察电极表面形貌。

电化学性能测试采用三电极体系,研究电极为工作电极,铂电极为辅助电极,参比电极为饱和甘汞电极。室温下用PAR-VMP3型恒电位仪和与其配套的EClab软件测定电极在0.5 mol/L H2 SO4溶液中不同扫描速度下的循环伏安曲线和动力学参数。

2 结果与讨论

2.1 SEM表征电极表面形貌

Ti/SnO2+Sb2 O x/PbO2电极中间层及活性层的SEM图像如图1所示。

图1 Ti/SnO2+Sb2O x/PbO2电极表面形貌(SEM)

从图1-a可明显看到SnO2+Sb2 O x中间涂层表面晶粒均匀细小、晶粒结合紧密无裂缝,这种结构可有效阻止活性氧原子的扩散,减少了二氧化钛绝缘层的形成,有利于延长电极使用寿命。从图1-b可见活性层表面呈蘑菇状,比表面积较大,有利于提高电极的催化活性。通过外观比较可明显看出,SnO2+Sb2O x比较致密,适合作钛基氧化物阳极的中间层,而PbO2氧化物适合作钛基氧化物阳极的表面活性层。

2.2 分形维数

材料表面的粗糙程度反映了它的表面活性面积的大小,且直接影响其电催化性能。Zuo[9]给出了描述粗糙分形材料表面的Weierstrass函数数学模型,见图2,函数形式为：

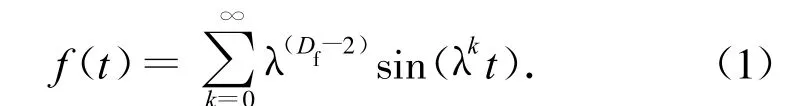
其中,λ=1.5,D f是分形维数,k=0～20。

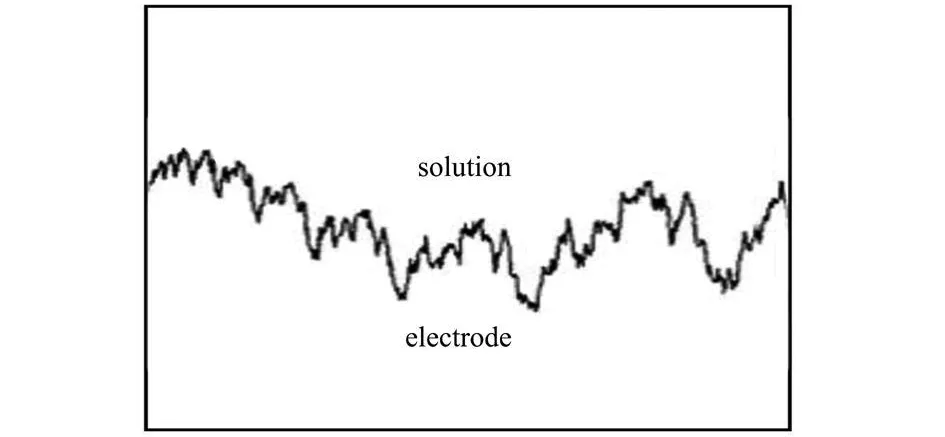
图2 粗糙分形电极剖面Weierstrass函数模型(D f=1.46)

根据图2,电极表面活性层的微观结构形态和粗糙度,可利用分形理论中的分形维数对其作定量描述,并获得催化反应性能与分形维数之间的关系。Pajkossy和Stromme等[10,11]用循环伏安法测定了材料表面的分形维数。在循环伏安法测定中,峰电流i p 与扫描速率的平方根v1/2存在如下关系[12]：

其中：A为电极面积,cm2;D 0为反应物扩散系数,cm2/s;c*0为溶液的浓度,mol/L;F为法拉第常数,9 650 C;R为理想气体常数,R=8.314 J/(mol◦K);n为电子转移数目;T为热力学温度,K;v为电流扫描速率,V/s。峰电流和扫描速率的关系为ip∝v1/2,如果考虑到分形因素的影响应有ip∝vα。根据不同扫描速率下的循环伏安图形,找出扫描速率与峰电流的对应关系,通过双对数关系图中斜率可求得α,而α是与电极分形维数D f相关的一个因子：

根据方程(3)可求得电极表面的分形维数D f：

Ti/SnO2+Sb2Ox/PbO2电极在不同扫描速率下的循环伏安曲线如图3所示,峰电流和扫描速率的对数关系如图4所示。

以图3-b为例分析扫描过程中的电化学反应。当扫描速率为20 mV/s时,在1.866 V出现一明显吸附峰I,生成PbO2-OH中间吸附态,且峰面积较大,说明羟基吸附量较大。从I点到Ⅱ点中间吸附态PbO2-OH快速氧化生成了高价态的PbO2-O,当扫描电位增加到2.005 V即Ⅱ点时,PbO2-O将分解生成原子氧O,原子氧O耦合生成氧分子O2,开始有氧气析出,可以观察到电极表面有气泡放出,电流越大放出氧气越剧烈。在正向扫描过程中随电极电势的增加电流逐渐增大,二者符合塔菲尔(Tafel)关系式,反向扫描时1.055 V出现一非常明显的还原峰Ⅲ,可能是电极氧化物本身发生还原反应,或是氧化反应析氧过程当中氧的脱附,或是二者同时存在。析氧可能的反应机理如下：

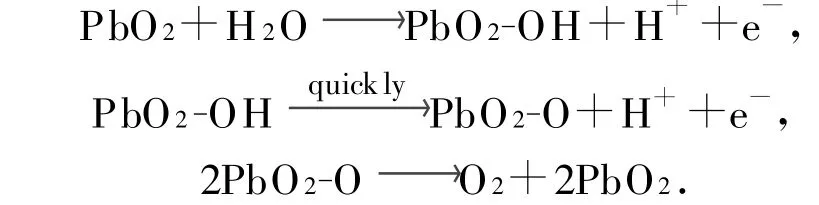
同理得到,当Sb掺杂摩尔分数为0.02,0.04,0.06,0.08,0.10时,Ti/SnO2+Sb2Ox/PbO2电极的析氧电位分别为2.035,1.999,2.005,1.980,2.025 V,因此Ti/SnO2+Sb2 O x/PbO2电极是酸性溶液中优良的高析氧电位的阳极材料。

图3 Ti/SnO2+Sb2O x/PbO2电极的循环伏安图

由图4及公式(3)求得：Sb掺杂摩尔分数为0.02,0.04,0.06,0.08,0.10时制得的 Ti/SnO2+Sb2O x/PbO2电极分形维数D f分别为：2.964,2.820,2.872,2.728,2.927。文献[13]中利用SEM图及计算机模拟计算出PbO2表面分形维数为2.281 7,可见上述两种方法均可定量表征氧化物电极表面的粗糙程度。作者认为,Sb的掺杂形成SnO2+Sb2Ox固溶体,不同Sb掺杂摩尔分数使得SnO2晶格参数和晶胞体积发生变化,在中间层SnO2+Sb2O x和活性层PbO2形成固溶体时,导致电沉积PbO2活性层表面粗糙程度有所不同,更深入的原因有待进一步的研究。

通过分析得到,当Sb掺杂摩尔分数在0.02和0.10时电极的分形维数较高。分形维数的增加表明电催化剂表面晶体的不规则凹凸形态增多,活性组分晶体表面的边、角、棱等缺陷增多。这些缺陷越多,缺陷之间的相互作用和造成的影响就越不能忽略,从而活性部位的产生几率和暴露机会增大[13]。此时,电催化剂的几何形态对催化剂产生主要作用,催化剂活性较高。

图4 Ti/SnO2+Sb2O x/PbO2电极峰电流和扫描速率的对数关系

2.3 动力学参数

在电极过程动力学中,衡量电极催化活性最重要的参数是交换电流密度。交换电流密度越大,则过电位越小,反应速度越快,说明电极电催化活性越高。为了全面地考察电极的电催化性能,从动力学方面对电极做了进一步的分析。

图5为Sb的摩尔分数分别为0.02,0.04,0.06,0.08,0.10时所得电极的析氧极化曲线即Tafel曲线。可以看出,电极电流密度的对数与电极电位有较好的线性关系,符合Tafel公式η=a+b lg j 0,其中η为超电势,a为单位电流密度下的超电势,b为Tafel斜率,j 0为交换电流密度。由此式可推得：

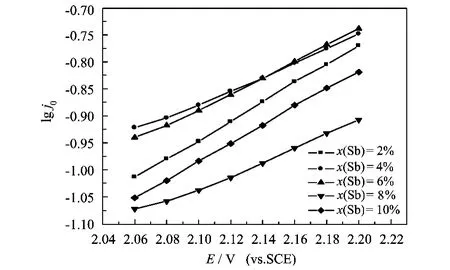
图5 Sb的掺入量不同时电极的Tafel极化曲线

图5中,电极析氧电位的高低顺序依次是Sb掺杂摩尔分数为0.02,0.10,0.06,0.04,0.08时,这与循环伏安图得到的析氧电位的顺序一致。电极的析氧电位存在差异是由于电极的中间层Sb掺杂摩尔分数不同,进而导致电极的结构及性能不同。由公式(4)可计算出,Sb掺杂摩尔分数为0.02,0.04,0.06,0.08,0.10时电极的Tafel斜率分别为0.759,0.792,0.769,0.815,0.764.Tafel斜率不同表明电极析氧反应的控制步骤存在差异。对曲线进行分析和数据处理得到电极动力学参数,从而得到电极在25℃时,在0.5 mol/L H2SO4中的动力学参数,如表1所示。

表1 不同Sb掺入量时电极的动力学参数

由表1和图5可知,当Sb摩尔分数为0.02和0.10时,a值较小,耗电量小,j 0值较大,反应速率较快。因此,本实验条件下电极的电化学催化活性较高的为Sb摩尔分数为0.02和0.10的电极。

3 结论

本文引入循环伏安法对Ti/SnO2+Sb2O x/PbO2电极表面的分形维数进行测定,对电极表面粗糙程度进行定量描述,讨论了分形维数与电极表面电催化性能之间的关系。当电极中间层Sb掺杂摩尔分数为0.02和0.10时其表面分形维数较高,且表面呈现蘑菇状,活性表面积较大,电催化活性较好;电极动力学参数a较小,j 0较大,反应速率较快。因此,Ti/SnO2+Sb2O x/PbO2电极是一种较理想的耐酸阳极材料。

[1] Trasatti S.Electrocatalysis in the anodic evolution of oxygen and chlorine[J].Electrochimica Acta,1984,29(11)：1503-1512.

[2] 童宏扬,王雅琼,许文林.Ti/TiO2膜电极在H2SO4和NaOH溶液中的电化学活化表面积[J].稀有金属材料与工程,2005(34)：1081-1084.

[3] Trasatti S.Physical electrochemistry of ceramic oxides[J].Electrochimica Acta,1991,36(2)：225-241.

[4] M andelbrot B B.The Fractal Geometry of Nature[M].New York：W H Freeman,1982：1-2.

[5] Go Joo-Young,Pyun Su-Il,Hahn Yoo-Dong.A study on ionic diffusion towards self-affine fractal electrode by cyclic voltammetry and atomic force microscopy[J].Journal of Electroanalytical Chemistry,2003,549：49-59.

[6] Pyuna S-I,Rhee C-K.An investigation of fractal characteristics of mesoporous carbon electrodes with various pore structures[J].Electrochimica Acta,2004,49：4171-4180.

[7] Pajkossy T,Nyikos L.Diffusion to fractal surfacesⅢ[J].Electrochimica Acta,1989,34(2)：181-186.

[8] Pajkossy T,Borosy A P,Martemyanov S A.Diffusion kinetics at fractal electrodes[J].Journal of Electroanalytical Chemistry,1994,366(1-2)：69-73.

[9] Zuo xiaobing,Xu changsen,Xin houwen.Simnlation of voltammogram on rough electrode[J].Electrochimica Acta,1997,42(16)：2555-2558.

[10] Stromme M,Niklasson G A,Ranqcist C G.Fractal dimension of insertion studies by diffusion-controlled voltammetry and impedance spectroscopy[J].Physical Review B,1996,54(5)：2968-2971.

[11] Isdorsson J,Stromme M,Gahlin R,et al.Ion transport in porous oxidefiles：cyclic voltammograms interpreted in termsof a fractal dimension[J].Solid State Communications,1996,99(2)：109-111.

[12] Bard A J,Faulkner L R.Electrochemical Methods Fundamentals and Applications[M].2nd Ed.John Wiley&Sons Inc,2001：231-232.

[13] 梁镇海,董黎君,陈新国,等.钛基氧化物电极的分形维数和电催化性能[J].催化学报,2001,22(2)：148-150.