NPC逆变器特定谐波组消除法

李涛，张晓锋，乔鸣忠

（海军工程大学 电气工程系，湖北 武汉 430033）

NPC逆变器特定谐波组消除法

李涛，张晓锋，乔鸣忠

（海军工程大学 电气工程系，湖北 武汉 430033）

针对传统特定谐波消除脉宽调制（SHEPWM）中所得触发角与调制比的非线性关系以及非线性超越方程组的困难求解，指出了SHEPWM中非线性超越方程组解的几何意义。基于此，设计了基于脉宽的谐波消除方法，仅需引入一个变量便可对任一次及其整数倍次的一组谐波进行消除。以5次组谐波和3次谐波消除为例，介绍了该方法在多个谐波消除中的应用，并对该方法所具备的谐波线性消除能力进行了分析。对所得结果进行谐波分析，证明该方法正确有效。

特定谐波组消除；非线性方程；谐波线性消除；NPC逆变器

特定谐波消除PWM（SHE）可消除任意特定谐波，但引入的非线性超越方程组求解困难。对此，可采用Newton-Raphson法，但有效性依赖迭代初值［1］。为提高有效性，可采用解轨迹微分预估初值［2］、三角载波初值［3］或初值解经验公式［4］等方法，但求解过程仍不确定。为提高确定性，可采用遗传算法［5］或混沌蚁群算法［6］，也可基于局部函数拟合［7］或 Walsh变换［8］将非线性方程线性化。可见，非线性超越方程组为SHEPWM的根本研究对象。

本文将非线性超越方程组的解与图形进行联系，指出了解的几何意义。结合三电平逆变器结构，设计出对某次及其整数倍次谐波（谐波组）进行消除的精确方法，并基于该方法进一步设计了以一定迭代计算次数获得对应精度、可消除一组和另外一次谐波的确定解法。通过对所得调制波进行谐波分析，结果证实了该方法的有效性。

1 非线性超越方程组其解的图形意义

1.1 信号形式及其傅立叶系数与图形的对应关系

周期信号可由傅立叶级数进行描述。本文将研究对象限定为即是奇函数又是奇谐函数的周期信号，即1／4周期信号［9］，本文称为奇奇谐信号，以消除余弦分量和偶次谐波分量［10］。

对任意频率和幅值的三电平脉宽周期信号，不失一般性，弧度范围取为［0，2π］，幅值取1，如图1a所示。由于信号线性可加，左方信号等同右方方波信号减去两组奇奇谐4脉冲信号（four pulse signal，PS4），如无特殊说明，下文所述PS4即为奇奇谐PS4。同理，任意调制比（modulation ratio，MR or md）下的脉宽信号可等同方波信号减去一系列PS4。基于此，本文用一组PS4控制一个谐波，进而消除该次及其整数倍次的谐波组（harmonic group，HG）。

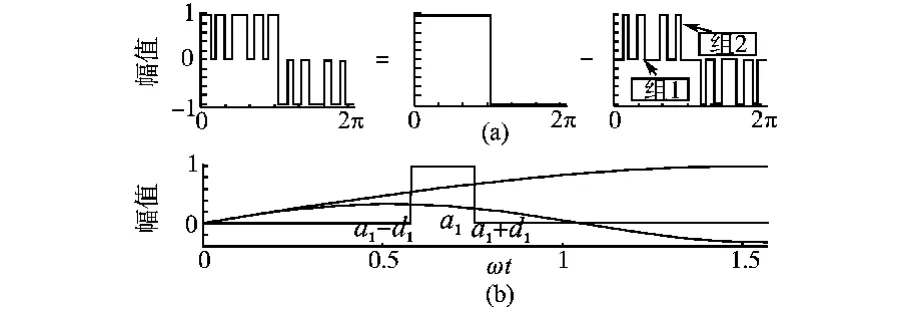
图1 信号分解与脉宽谐波Fig.1 Signal decomposition and pulse harmonic

对图1b四分之一周期信号，［a1-d1，a1＋d1］上脉宽对应的周期信号傅立叶系数为

其中，n为谐波次数，下标1表示该值对应第1组PS4，对方波信号，a1＝d1＝π／4，有f（nω）＝4／（nπ）。

由式（1）第3行，n次谐波幅值等于谐波函数在［a1-d1，a1＋d1］上的面积乘以4／（nπ），且该幅值与该范围的谐波面积恒比为4／π。因此，一组PS4中各谐波幅值与其限定的谐波函数面积一一对应。

1.2 方程组解的图形意义

非线性超越方程组的解确定的脉宽输出谐波幅值为零，即当输出波分解为方波与各PS4后，各PS4对应式（1）第3行中的积分项之和为1。因此，只要某组角度限定范围内的谐波函数面积为1，则该组角度必为非线性超越方程组的解。

2 特定谐波组消除法（SHGE）

2.1 组消除法基本原理

由式（1），将各次谐波幅值除以方波中对应次数谐波的幅值，有md取为输出基波与方波所含基波的幅值之比

不失一般性，以3次HG（HG3）消除为例，令n3＝3（n3可同时视为任一奇数），则引入2组PS4便可控制基波大小并消除HG3。当md由1连续下降，将包含2个阶段，阶段划分与算法策略见2.3节。

1）谐波无法完全消除阶段。该阶段仅需引入一组以0为起点的PS4进行调制，如图2a所示，且a1＝d1，a1＋d1为待求触发角，算法如下。

图2 谐波消除阶段示意图Fig.2 Scheme for phases of harmonic elimination

令该PS4基波分量为1-md，由式（2）并结合约束条件，有

解之得

当a1＝d1＝0.5×0.5π／n3时该阶段结束，有

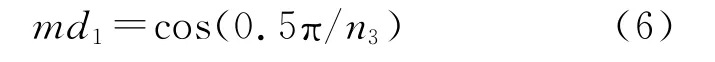
其中，md1为该阶段md下限。当md＝md1，有

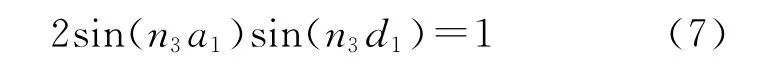
即当md从1降至md1，PS4与方波信号中的n3次谐波首次完全抵消。

2）谐波完全消除阶段。当md降至该阶段，为调整基波幅值并保持谐波消除状态，需引入另一组PS4，如图2b所示。其中a2＝0.5π／n3×2，即n3次谐波过零点，a1＝d1≡0.5×0.5π／n3，未知量仅为d2。令两组PS4中基波总量为1-md，n3次谐波总量为1，由式（2），有

由1.2节，引入的第2组PS4与方波信号所含3次谐波分量相等，即有sin（n3a2）≡0。

代入已知条件，得

2.2 谐波组的消除状态

对HG3所含谐波，图2中PS4的奇奇谐特性使其仅含n3的奇数倍谐波，次数为n3＋2kn3，k＝1，2，…。当md＝md1，HG3被完全消除，图2下方左端脉宽与方波含等量n3次谐波。由于n3＋2kn3次谐波关于n3次谐波零幅值所在非零弧度点（如a2）奇对称，故引入PS4的中心位置使该PS4不含n3＋2kn3次谐波量。故当md＜md1，各组PS4所含n3＋2kn3次谐波总量与方波相等，如图1上方反向合成后，输出波形将不含HG3。

2.3 谐波无法完全消除阶段的角度选择策略

谐波未完全消除时，随md递减，所选最优策略应使待消除谐波相对于基波衰减速度得到最快消除。结合谐波幅值与谐波函数面积积分的对应关系以及图1中信号分解的观点，可由微积分原理确立最优策略。

谐波衰退即其幅值减小，而幅值减小量等价于图1bPS4限定的横坐标段与谐波函数曲线围成的面积，如式（1）所示。同时，任意脉宽输出中某次谐波幅值的减小量可视为在方波中减去一定量的某组PS4。因此问题归纳为：随md递减，从方波中一一减去某组宽度极窄的PS4，该极窄PS4将使待消除谐波相对基波衰减速度得到最快消除。极窄PS4可视为工程应用中硬件限定的最窄输出脉宽，本文视为宽度无穷小的固定PS4。对n3次谐波消除，若某处极窄PS4中n3次谐波幅值与基波幅值的比值大于其他极窄PS4，则从方波中减去该处PS4即为上述问题的解。因此，取极窄PS4所含n3次谐波幅值与基波幅值的比值为指标，随md递减，从方波中一一减去该指标由高至低的极窄PS4即为最优选择。

对图1下部PS4，令a1-d1＝a，a1＋d1＝b＝a＋ε，ε为正无穷小。该PS4中n3次谐波与基波基于式（2）的幅值分别为cos（n3a）-cos（n3b），cos（a）-cos（b），a，b∈［0，π／2］。设两者比值为y，则

由于［0，0.5π／n3）、［0.5π／n3，π／3）和［π／3，π／2）内都存在使极窄PS4限定的横坐标段与3次谐波函数所围面积相等的a，而相应区间上基波函数面积却依次增大，故a∈［0，0.5π／n3）上的y值大于其他分区间。由式（10），y在［0，0.5π／n3）内递减。故在谐波无法完全消除阶段，最优策略应引入一组如图2上方满足a1＝d1的PS4，随md减小，不断增加d1直至a1＋d1＝0.5π／n3。

2.4 单次谐波完全消除的临界调制比

对任何谐波消除理论，若仅消除n次谐波，由2.3节最优策略及式（4），可完全消除n次谐波阶段对应的最大md（即临界值md0n）符合式（11），当md＞md0n，n次谐波将无法消除。

3 次数互质的两种谐波消除

3.1 基本原理

基本原理可概括为：基于某次HG消除，同时消除次数与该次互质的谐波。以HG5和3次谐波消除为例，见图3。令n5＝5，n3，n5可同时视为任意两种互质的谐波次数。

图3上部为n5次谐波组（HGn5）完全消除的临界状态；中部为HGn5完全消除、n3次谐波未完全消除状态，有md∈（md03，md05］，且增加一组PS4调节基波大小；下部为HGn5和n3次谐波完全消除状态，为维持HGn5的完全消除状态并消除n3次谐波而引入第3组PS4。

该谐波消除方式以消除HGn5为基础，同时利用PS4的剩余调节能力消除其他次谐波。在区间（0，π／2）上，n次谐波过零点有（n-1）／2个。由于HGn消除中引入的PS4位于n次谐波过零点以不含HGn，相对于谐波无法完全消除阶段，谐波完全消除阶段将增加（n-1）／2组PS4，如HGn3增加1组，HGn5增加2组。同时，增加1组PS4可额外消除一个谐波，在HGn消除中，除一组PS4用于控制md，其他各组PS4可消除（n-3）／2个次数与n互质且低于n的谐波，如HGn5消除，可消除1个与n5互质且低于n5的谐波即n3次谐波。由于HGn消除法引入的PS4必须位于n次谐波过零点，而该过零点无法满足次数与n互质的HG消除的要求，因此对于互质组，引入的PS4必增加互质组中未被控制的谐波。由各次谐波过零点个数及md0n随n的单调性，若基于低次HG消除高次谐波，为使低次HG得到最快消除，必在高次谐波可完全消除阶段重现可消除的高次谐波。故基于某次HG消除去消除次数与该次互质的谐波，应基于高次HG消除且可消除（n-1）／2个较低次数的谐波。

因此，对n5次HG和n3次谐波进行消除，触发角共分为（n5＋1）／2个阶段。

1）各谐波无法完全消除。变量分布如图3a所示，具体计算参见式（4）及其相关结论，其中md下限为：md1＝cos（a1＋d1），a1＝d1＝0.5×0.5π／n5。

2）n5次（高次）HG完全消除n3次（低次）谐波未消除。变量分布如图3b所示，各变量满足

其中a1＝d1＝0.5×0.5π／n5，a2＝0.5π／n5×2，d2为待求变量。此阶段md下限即md03，且有

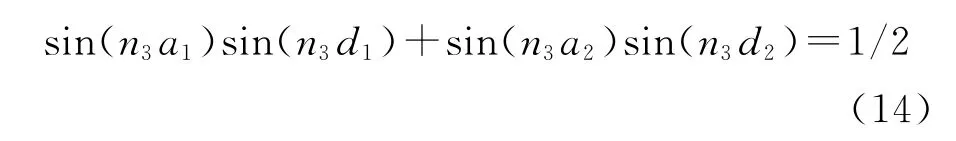
由式（13）、式（14）可得d2和本阶段md下限md2。

3）5次（高次）HG和3次（低次）谐波完全消除。变量分布如图3c所示，各变量满足

其中a1＝d1＝0.25π／n5，a2＝π／n5，a3＝2π／n5，d2，d3为待求变量。由于含2个未知量，上式为二阶非线性超越方程组，可采用传统SHEPWM中的相关算法进行求解。然而，由式（15）第1等式，各PS4的宽度变量（如d3）在区间［0，π／2）内，正弦函数在该区间单调递增。因此PS4越宽，PS4中基波量越大，相应md越小，即图3中脉宽越宽，限定的角度范围越大，范围内所含基波积分面积越大。利用该单调性，可采用二分法对式（15）进行迭代求解。

图3 5次组3次谐波消除阶段Fig.3 Scheme for phases eliminated，3th and group 5th

3.2 迭代步骤与计算误差

对n（奇）次HG消除，PS4位于n次谐波过零点，在（0，π／2）中为2k×0.5π／n，k＝1，2，…，（n-1）／2，脉宽范围为［0，0.5π／n］。对确定的md，令d2＝d21＝（0＋0.5π／n）／2，下标1代表第1次迭代。仍以5次HG和3次谐波消除为例，为消除3次谐波，最终解必满足式（15）第2等式，将d21代入该式，得d31，再将d21，d31代入第1等式左方并与右方比较大小，若左方＞右方，由单调性，d2过大，取d2＝d22＝（0＋d21）／2，否则，取d2＝d22＝（d21＋0.5π／n）／2。在第m次迭代中，所得解与精确解的误差err满足

同时，由于d2初始值为式（14）确定的某个非零值，假设此值为d20，则第m次迭代所得解与精确解的误差errm进一步满足

对于仅消除n（n＞3）次HG，只需一组PS4进行控制，PS4中点可位于任一过零点，但为具有最少开关次数，增加的PS4应能与已有PS4合并。如图3c对5次HG的消除，应先增加a2组，待a2组同a1组合并后，再依次增加右方毗邻的一组PS4即a3组。

按以上计算原理可消除n次HG及次数低于n的一个谐波，并可根据所需弧度精度确定计算迭代次数。然而迭代计算仍具有较大的计算量，为减少计算量，可对基于该原理所得结果进行线性拟合，这也是HG消除的另一重要特性，见第5节。

4 算法验证

4.1 3次谐波组消除

由2.1节所述方法进行PWM，输出脉宽中各谐波幅值同md的关系见图4，横坐标为md，纵坐标为各次谐波相对方波幅值为1时的幅值。可见，当md大于式（6）也即md＞md03＝0.866，3次HG无法完全消除。在该阶段，随md递减，由于采用2.3节最优策略，各谐波在md03处被首次消除。当md＜md03，3次HG保持完全消除状态，其他谐波则处于波动状态。

图4 3次谐波消除时各谐波幅值Fig.4 Harmonic amplitude，group 3th eliminated

4.2 3次、5次组谐波消除

图5 5次组和3次谐波消除时各谐波幅值Fig.5 Harmonic amplitude，group 5th，3theliminated

5 谐波线性消除

5.1 计算结果的线性分析

3.1节迭代运算的最大脉宽值为0.5π／n5，图6为［0，0.5π／n5］上的谐波函数。可见，该区间内基波函数十分接近线性函数，有sin（x）≈x。对于sin（n3x），由于弧度放大n3倍，取sin（n3x）≈n3x将使误差随弧度增加而显著增大，但由最小二乘拟合，该函数线性特征仍十分明显。因此，式（15）第2等式中未知量d2，d3代入该式第1等式后，将使变量同md也具有近似的线性关系。当n5增大，低于n5次的谐波函数将随波次递减而具备更强的线性。

图6 谐波函数线性示意图Fig.6 Scheme of linearity of harmonic function

所得各脉宽随md的变化见图7，图7中点线为10次迭代所得高精度离散脉宽值，与之几乎完全重合的实线为各阶段线性拟合线。可见随md递增，PS4个数及各脉宽值递减，在谐波消除的不同阶段中，脉宽具有很好的线性变化规律。

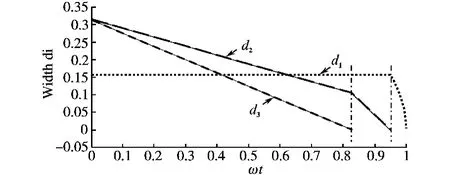
图7 3次、5次组谐波消除脉宽变化图Fig.7 Pulsewidth variecy，group 5th，3theliminated

另外，若基于低次HG去消除高次谐波，由于高次谐波函数sin（mx）中mx∈［0，0.5π／n×m］，m＞n，谐波函数将为非单调函数，有明显的非线性。故3.1节基于高次HG消除低次谐波的策略不但利于谐波消除，且利于最终结果的线性化。

5.2 谐波线性消除

由5.1节，可见HG消除法对脉宽触发角具有线性调制的特点，可对结果进行线性拟合并利用拟合函数代替触发角度的迭代计算。对3.1节5次HG和3次谐波消除，有如下计算。

1）谐波无法完全消除。取a1＝d1＝π／20，得本阶段md下限md1为

2）5次谐波组已消除且3次谐波未消除。取a1＝d1＝π／20，a2＝π／5，由式（14），得

代入式（13），得本阶段md下限md2为

3）5次谐波组和3次谐波完全消除。取a2＝π／5，a3＝2a2，a1＝d1＝π／20。当md∈［0，md2），有

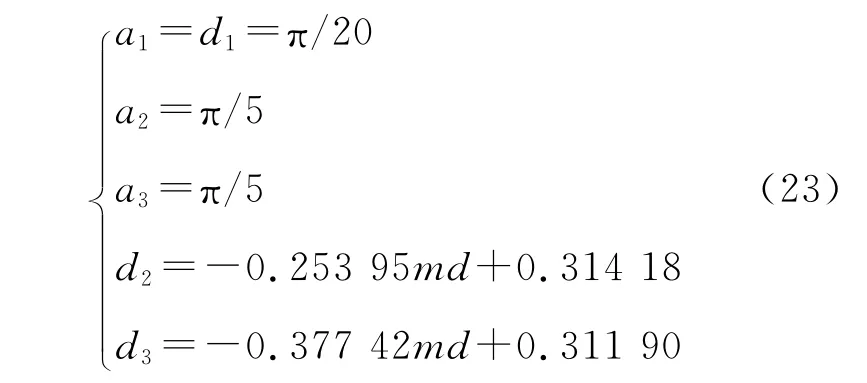
由式（19）、式（22）与式（23）计算触发角，所得输出脉宽的谐波含量见图8。图8中虚线为迭代法输出结果，实线为拟合公式输出结果。可见，线性拟合公式可完全取代有限次迭代计算。因此，除在谐波无法完全消除阶段采用一次反三角运算，其余阶段都可通过线性运算以获得各脉宽位置和脉宽宽度，进而确定脉宽触发角，无需迭代或非线性运算，利于实时计算。

图8 线性拟合前后谐波变化对照图Fig.8 Pulsewidth variety，linear fitted／unfitted

6 结论

传统SHEPWM基于n个触发角控制n个谐波，消除n个谐波需n＋1个变量，使描述谐波的三角函数具有的非线性直接传递到触发角同md的变化关系中。为计算触发角，须进行n＋1阶非线性超越方程组的迭代求解。本文提出的SHGEPWM基于脉宽控制脉宽，通过一个触发角变量描述的脉宽所蕴含的一系列谐波对HGn进行消除。若用于消除n个次数互质的谐波，可基于高次HG消除低次谐波，通过对脉宽位置的合理限定，需求解的非线性超越方程降为n阶。由于采用脉宽取代单触发角进行谐波消除，牺牲一定的脉宽数以利用脉宽所含各谐波函数非线性的相互遏制性，使最终所得触发角随md呈线性变化规律。通过离线求解非线性超越方程组，将所得触发角随md的变化规律进行线性拟合，可实现谐波的线性消除。

［1］ Sirisukprasert S.Optimized Harmonic Stepped-waveform for Multi-level Inverter［Z］.Master thesis，1999at Virginia Polytechnic Institute.

［2］ 刘文华，宋强，陈远华，等.NPC逆变器SHE-PWM开关角度的计算方法研究［J］.中国电机工程学报，2002，22（11）：31-34.

［3］ 张艳莉，费万民，吕征宇，等.三电平逆变器SHEPWM方法及其应用研究［J］.电工技术学报，2004，19（1）：16-20.

［4］ 张永昌，赵争鸣.三电平逆变器SHEPWM多组解计算方法［J］.电工技术学报，2007，22（1）：74-78.

［5］ Maswood A I，Wei Shen，Rahman M A.A Flexible Way to Generate PWM-SHE Switching Patterns Using Genetic Algorithm［J］.Applied Power Electronics Conference and Exposition，Sixteenth Annual IEEE，2001，2：1130-1134.

［6］ Hu Cungang，Wang Qunjing，Jiang Weidong，etal.Optimization Method for Generating SHEPWM Switching Patterns Using Chaotic Ant Colony Algorithm Applied to Three-level NPC Inverter［C］∥Proceeding of International Conference on Electrical Machines and Systems，2007：149-153.

［7］ Ali I Maswood.PWM SHE Switching Algorithm for Voltage Source Inverter［C］∥Power Electronics，Drives and Energy System，International Conference on，IEEE，2006，12：1-4.

［8］ 郑春芳，张波.基于Walsh变换的逆变器SHEPWM技术［J］.电工技术学报，2005，20（5）：65-71.

［9］ 张永昌，赵争鸣，张颍超.三电平逆变器SHEPWM多组解特性比较及实验［J］.电工技术学报，2007，22（3）：60-65.

［10］潘双来，邢丽冬.信号与线性系统［M］.北京：清华大学出版社，2006.

Selected Harmonic Group Elimination for NPC Inverters

LI Tao，ZHANG Xiao-feng，QIAO Ming-zhong

（DepartmentofElectricalEngineering，NavalUniversityofEngineering，Wuhan430033，Hubei，China）

Aims at the nonlinear relationship between trigger angles and modulation index derived by traditional SHEPWM as well as the difficulty to solve the nonlinear transcend equation group，the geometry meaning of the roots of nonlinear transcend equation group in SHEPWM was indicated.With this meaning，harmonic elimination methods based on pulse-width was derived.Only by using one variable，harmonic of certain frequency as well as frequency of integral times can be eliminated.By citing elimination of harmonic 3thand group 5th，the application of this method to multi-harmonic elimination was introduced.The abilities of this method to eliminate harmonic linearly was analyzed.The harmonic analysis of the results proves the validity and efficiency of this method.

selected harmonic group elimination（SHGE）；nonlinear equation；linear harmonic elimination；NPC inverter

TM464

A

国家自然科学基金（50277008）

李涛（1981-），男，博士研究生，Email：tao＿lyy＠yahoo.com.cn

2010-10-17