水田井灌区的优化设计

陈凌颜，滕 凯

(1.黑龙江省齐齐哈尔市河道管理处，齐齐哈尔 161006;2.黑龙江省齐齐哈尔市水务局，齐齐哈尔 161006)

1 问题的提出

上世纪80年代以来，由于水田面积的连续递增而使地表水资源利用日趋紧张，为了进一步扩大水田面积，各地均先后建起了不同规模的水田井灌区，而作为井灌区建设的主要依据——井灌规划，如何才能实现优化设计，则是水田井灌区获得最高运行效益的关键问题。我们知道，单井的灌溉毛效益与该井设计涌水量成正比，而在一定的水文地质条件下设计涌水量的增大又将使成井造价和年运行费用提高，因此，如何确定单井的设计涌水量，成井深度、成井直径及布井间距，就成为井灌区优化设计的首要问题。常规的井灌区规划往往是在已知某一水文地质条件下，参照已成井或根据经验初拟单井的涌水量(或灌溉面积)及成井直径，进而计算出成井深度及布井间距。实践证明，由于这样的规划存在较大程度的经验性，因而是所建井灌区或是不能充分发挥效益，或是年运行费用较大，或是成井造价过高。针对这一问题，本文根据干扰井群的水力计算原理，以现值效益理论为基础，通过数学分析的方法，提出了井灌区优化设计的基本计算公式和求解方法，对井灌区的优化设计具有一定的实际意义。

2 公式的推导

2.1 基本目标函数

根据井灌区的规划特点，取公顷灌溉净效益(纯效益)最大为非线性规划的目标函数，其数学表达式应为:

式中:C、V1、F1分别为年平均公顷净灌溉效益、毛效益及费用支出;元/hm.a。

为分析问题方便，现将式中的有关项目分解如下:

(1)年公顷毛效益

水田井灌区增收的毛效益主要取决于水稻的产量及旱改水前旱田的产量，可用下式表示:

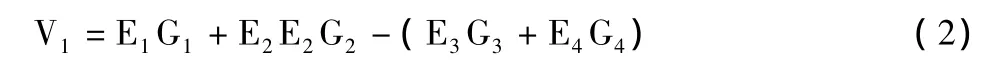
式中:E1、E2和G1、G2分别为水稻及稻草的年公顷产量(kg/hm·a)和水稻及稻草的单价(元/kg);E3、E4和 G3、G4分别为改水田前旱田的年公顷粮食及杆棵产量(kg/hm·a)及相应的单价(元/kg)。

(2)年公顷费用支出

水田井灌区增加的年公顷费用支出可按下式计算:

式中:Fs、Fh分别为水田及旱田的年公顷费用支出，元/hm·a。因旱田的年公顷费用支出Fh可按下式计算:

式中:Wi(i=1，2，3，4)分别为旱田的年均公顷种子、化肥农药、人工及机械费，元。

根据井灌区年费用支出项目的组成，每公顷水田应分摊的费用主要有折旧费、大修费、机泵运行费及农业生产费，其表达式为:

式中:Ci(i=1，2，3，4)分别为年公顷均折旧费、大修费、运行费及生产费，元/hm·a;可分别按下式计算

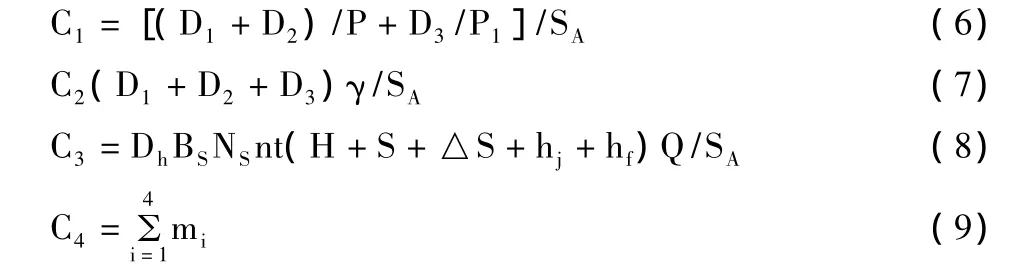
其中:D1、D2及D3分别为钻孔费、井管费及机泵设备费，元;SA为单井实灌面积，hm;Dh为中间变量;P1、P分别为机泵及井的使用年限，a;Q为单井设计涌水量，m3/h;为费用年提取比例，%;n、t分别为井的年工作天数(d/a)及天工作时间(h/d);mi(i=1，2，3，4)分别为水田的年均公顷种子、化肥农药、人工及机械费，元;D1、D2、D3、SA及 Dh可分别按下式计算

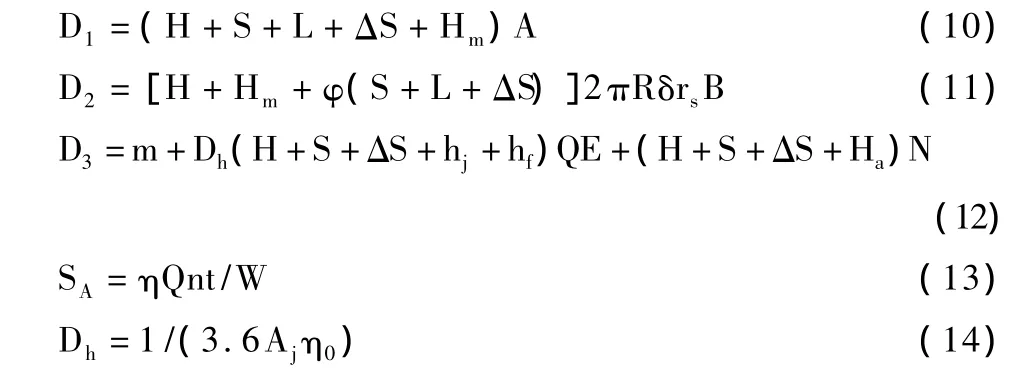
式中:η为渠系有效利用系数;W为水稻公顷灌水定额，m3/hm·a;η0为机泵总装置效率;Aj为配套系数，柴油机取75、电动机取102，kg·m/s;BS 为额定燃油量，kg/马力;NS为电或柴油单价，元/kg;H为与灌溉设计保证率相对应的灌溉期地下水潜水位的加权平均地下水位埋深，m;Hm为沉砂管长，m;S、L及 分别为潜水位降深、动水位以下花管长及井损值，m;E为单位马力机泵配套费，元/马力;m为动力配套土建费用，元;R、D分别为井半径和滤水层厚，m;A为成孔进尺费，元/m;为花管造价增加系数;、rs及B分别为管壁厚(m)、管材容量(T/m3)及单位重造价(元/T);hj、hf分别为出或吸水管的局部及沿程水头损失，m;N为出水或吸水管的单位长度造价，m。

H、S、L、、hj及 hf可分别按下式计算:

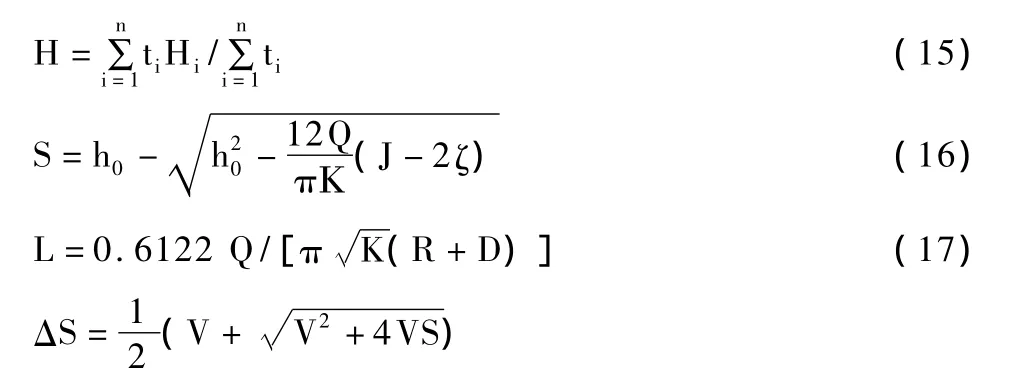
式中:为与灌溉设计保证率相对应的潜水层灌溉期的加权平均地下水位埋深，m;tiHi为第i次灌水历时(h)与相应的平均地下水位埋深(m)的乘积;h0为潜水层灌溉期的加权平均厚度，m;Ha为淹于水井中的吸水管长，m;为出或吸水管的半径，m;f及分别为沿程摩擦系数及局部阻力系数和;K为渗透系数m/d;为经验系数，砾石滤水取15～25，金属丝滤水取6～8，不完整井将扩大1.25～1.5倍;V为中间变量;J为干扰井函数;为潜水井的布完整系数(查表1)。J、V可按下式计算

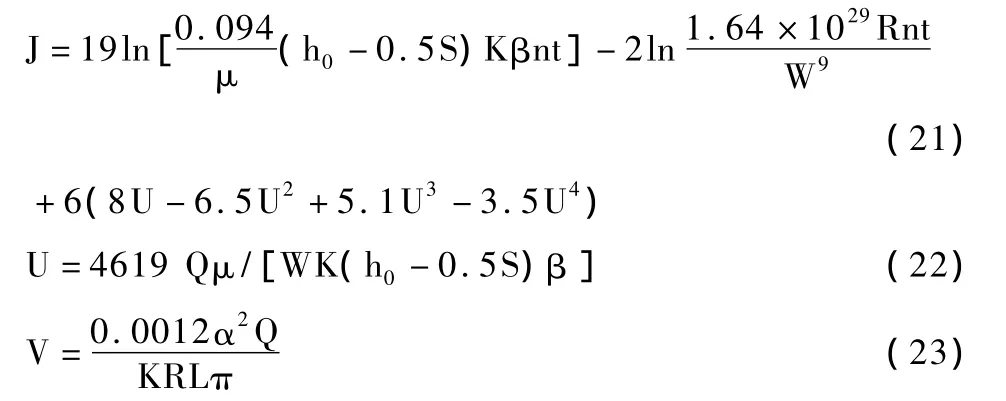
式中:β为不连续抽水影响系数;μ为给水度。

表1 ζ值表

2.2 约束条件

(1)设计典型年内井灌区总开采量应小于或等于允许开采量，即:ntnjQ≤Wc

式中，nj为井灌区内的布井眼数，眼;Wc为灌区控制面积内的地下水允许开采量，m3。

(2)水田的一次灌水定额小于或等于水田的总涌水量，即:TiQ≥WP

式中，Ti为水田某次灌水总历时，h;Wp为水田在Ti时段内的总设计灌水量，m3。

(3)有效成井深度(不包括沉砂管长)应等于或小于不透水层的埋深，即:

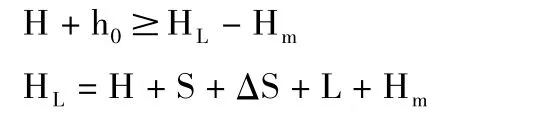
式中，HL为成井总深度，m;其他符号同前。

3 最优设计井参的求解

因最优设计井参的表达式为较复杂的隐函数，可采用逐次逼近法进行求解，为加快解算速度，在求解之前可用BASIC语言编制电算程序，利用计算机进行求解(因受篇幅所限，程序略去)。现就主要的求解步骤简述如下:

(1)统计并分析规划井灌区内长系列的年及灌溉期的地下潜水位埋深及其变化规律，进而求出与设计灌溉保证率相应的地下水位埋深代表年，并由设计灌溉制度求出灌溉期的单井年工作天数及工作时间。

(2)借助钻探资料确定潜水含水层的渗透系数K、给水度及隔水底板的埋深等参数。

(3)根据当地井灌水田的经济效益及成井费用合理确定出水稻的产量、单价、成井材料费、机泵配套费、油或电的单价、机井及机泵的使用年限，大修、维修管理费的年提取比率值等。

(4)如果受钻井设备或井管材料所限，在成井直径已经确定的情况下(定井径)，可先初设涌水量Q1及潜水降深S1求出L，并根据和查表1确定值，然后即可利用式(16)通过逐次逼近求出 S，再根据 Q1和 S求出 L、ΔS、hj及 hf值，同时完成约束条件的核对。

(5)根据上述所求各值即可求出在已定成井直径R，涌水量为Q1情况下的单井年公顷纯效益C1。

(6)再设用水流量为 Q2，使 Q1+ΔQ，完成步骤 4.、5的计算求出C2，如C2＞C1，再设Q3=Q2+ΔQ，继续进行逼近计算，直至求出 maxC(反之，如果 C2＜C1，则重设 Q2=Q1－ΔQ)，获得最优设计涌水量Q及井深HL。

(7)如成井直径不受施工及材料条件限制，可先初设成井半径R1，并采用与上述同样的方法求出最大纯效益C1，调整初设成井半径R2，使R2=R1+ΔR，求出在井径为R1+ΔR情况下的最大纯效益C2，比较C1、C2值的大小即可采用与步骤6相同的逼近法求出不定井径情况下的最优设计井参。

4 设计举例

现分别给出几种不同水文地质条件下的水田井灌区设计参数。采用本文所推荐的方法笔者完成了当水田的亩灌水定额为750 m3/亩.a，年工作 50 d、每天抽水 14 h、每眼井(包括井房)固定投资为3 000元情况下的定井径和不定井径优化设计井参的计算，优化成果见表2及表3。

表2 定井径优化设计成果表

表3 不定井径优化设计成果表

5 结语

(1)水田井灌区的效益与灌水技术、成井造价、年运行费用及成井设计参数有着密切的函数关系，而井灌区的常规设计方法则由于没能将这些函数关系进行综合考虑，致使井灌区的设计井参极不合理，或使成井造价过高，或使年运行费用消耗较大。因此，该文所述及的优化设计方法对提交合理的规划设计、提高井灌区的经济效益具有一定的实际意义。

(2)从优化设计井参的求解公式可以看出，成井含水层的渗透系数K及给水度μ对优化设计井参值的影响很大，因此，在进行井灌区的优化设计之前，应尽量采用试验井求解出较符合实际情况的K及μ值，以使优化设计更趋于合理。

(3)该优化设计是根据水田井灌区规划设计对地下水开采要求的特点，而提出的井参优化，即最优化设计涌水量，成井直径、成井深度及成井密度。有关机泵的合理配套请参见有关文献确定，本文不作详述。

［1］施普德.井水量计算的理论与实践［M］.地质出版社，北京:1977－02.

［2］刘兆昌，朱琨.供水水文地质［M］.中国建筑工业出版社，北京:1979－12.

［3］西北农学院，华北水利水电学院.地下水利用［M］.水利出版社，北京:1981－12.

［4］丛培善.排灌机械配套手册［M］.中国农业机械出版社，北京:1982－12.

［5］赵尔慧，张建山.井泵配套的优化法［J］.地下水:1988－ (3).

［6］李寿生.灌溉经济与最优化技术［M］.上海交通大学出版社，上海:1987－09.