基于特征模型的高超声速飞行器姿态控制器与自适应滤波算法的设计*

王丽娇

(1.北京控制工程研究所，北京 100190;2.空间智能控制技术重点实验室，北京 100190)

高超声速飞行器飞行过程环境极为复杂，动力学模型也较为复杂，是一个非线性、强耦合、快时变且具有很大不确定性的复杂系统，这都为控制器的设计提出各种挑战.目前，国内外很多学者都在从事这方面的研究，分别从滑模控制、鲁棒控制、模糊控制、神经网络控制等方面研究了高超声速飞行器的飞行控制问题［1-4］.但目前的这些研究均没有考虑飞行过程中的滤波问题.

基于特征模型的全系数自适应控制方法是吴宏鑫院士［5］提出的一套完整的实用性很强的理论和方法.特征模型理论在原来复杂的动力学模型的基础上抓住系统输入输出的主要关系，将原高超声速飞行器的复杂动力学模型压缩为考虑控制要求的更为简洁的特征模型，使得控制器设计大大简化.基于特征模型的自适应控制得到广泛研究，并取得了重要进展［6-7］.

目前，基于特征模型的高超声速飞行器姿态控制采用的都是梯度法进行参数辨识，且没有考虑测量噪声的影响.实际上，高超声速飞行过程中，测量过程引入的大气扰动需要作为测量噪声处理，耦合的弹性模态振动、高超声速大动压会引起舵面颤振等都会将测量噪声引入控制回路［8］.考虑测量噪声时，既要通过设计全系数自适应控制器保证系统闭环稳定，又要通过滤波对噪声有效抑制，从而实现对姿态的精确跟踪和保持.

实际上，原高超声速飞行器复杂的非线性反映在其特征模型参数的时变性上，这导致了基于特征模型的滤波模型的非线性.特征模型的参数与系统状态及模型密切相关，噪声信号被包含到状态量中，特征模型的噪声统计特性与实际过程的噪声统计特性有较大差异，从而造成很大的模型不确定性.此时，非线性系统滤波中得到广泛应用的扩展卡尔曼滤波(EKF)将存在精度不高、甚至发散等不足.

为了克服上述缺点，粒子滤波(PF)、STF和UKF应运而生.PF计算量非常大，很难满足高超声速飞行器快速机动性的需求.STF是一种效果很好的自适应滤波器，具有极强的模型失配的鲁棒性，可以在线调整滤波增益，从而达到算法自适应的目的［9］.但STF的基本理论框架是建立在EKF基础上的，因此它具有EKF的所有缺点.UKF无需用线性化手段就可以对非线性系统进行处理，可以达到和线性KF相媲美的性能.但是传统的UKF缺乏自适应能力，国内外的学者提出了很多改进的UKF算法，以提高UKF算法的估算精度［10-11］.

本文在STF和UKF的基础上，提出了一种基于特征模型的闭环滤波算法，并结合非线性黄金分割自适应控制律，将其应用于含测量噪声的高超声速飞行器的参数辨识与控制中.仿真结果验证了该方法的有效性.

1 高超声速飞行器的单通道特征建模与控制

所谓特征建模，就是将对象动力学特征和控制性能要求相结合进行建模，而不是仅以对象精确的动力学分析来建模［5］.特征模型在原模型的基础上提取输入输出的主要矛盾，把其他次要因素压缩到系统参数中.文献［7］用12个互相耦合的非线性微分方程给出了高超声速飞行器无动力巡航段的六自由度动力学模型，并针对此复杂动力学模型建立了含耦合的多输入多输出特征模型，在此基础上为了进一步简化设计，通过指令滤波或者减小控制器增益的方法降低滚动角速度，以避免由于较大的滚动角速度造成通道间动力学的严重耦合，从而可以采用三通道解耦的方案对高超声速飞行器的姿态进行特征建模.以升降舵、副翼、方向舵为输入，以攻角、滚转角和侧滑角为输出，原复杂的非线性动力学模型可以用如下的三输入三输出的二阶时变差分方程组来等效表示:

α，β，φ分别为攻角，滚动角和侧滑角系统输出，αf，βf，φf为 3 个姿态角的滤波输出，δe，δr，δa分别为升降舵、方向舵和副翼的舵偏，由于3个通道是独立的，因此我们将每个通道写成:

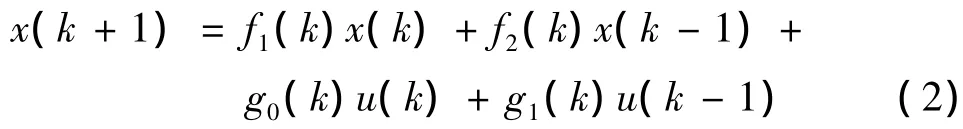
为了提高过渡过程的跟踪能力，采用非线性黄金分割控制器［8］设计全系数自适应控制律.参数辨识结果记为，进而设计全系数自适应控制律:u=ug+uo+ui+ud.

式中，η1，η2为正常数，μ为常数.令

非线性比例系数Kp(k，y(k))不仅与kp(k)有关，而且会随着|y(k)|的变化而变化，变化的情况与 η1，η2，μ 有关.

ki1，ki2，cd，ld为所需调整的参数，yr(k)为跟踪目标函数.uo，ug，ui，ud分别称为维持/跟踪控制律、黄金分割控制、逻辑积分控制和逻辑微分控制.

2 滤波算法

2.1 STF

STF是周东华等［12］提出的一类自适应滤波器，是在卡尔曼滤波的基础上发展起来的.卡尔曼滤波关于模型不确定性的鲁棒性比较差，当系统模型参数与实际过程参数存在较大差异时，其估计精度会大大下降，甚至发散.

与通常的滤波器相比，STF具有以下优点:

1)较强的关于模型参数不确定性的鲁棒性;

2)极强的关于突变状态的跟踪能力;

3)适中的计算复杂度.

为了实现STF，周东华等提出了一个正交性原理:通过在线选择一个适当的时变增益阵K，使得在满足扩展卡尔曼滤波器的性能指标的同时满足不同时刻的残差序列处处保持相互正交的要求，即E(r(k)rT(k))→min，其中r(k)为残差.

STF的一种实现算法是引入多种渐消因子Λ，通过调整Λ来实时调整状态预报误差的协方差，从而达到调整滤波增益矩阵以形成STF的目的［12］.其具体算法见式(17).

2.2 UKF

UKF主要用于对非线性系统的状态和参数进行观测，EKF只是简单地将非线性对象模型线性化，然后再利用线性卡尔曼滤波方法，它给出的是最佳估计的一阶近似.UKF主要是使用无迹变换［10］以确定性的“采样”方法计算随机变量的统计特性(均值和方差).其计算的均值和协方差可以准确到二阶，不仅提高滤波器的估计精度，而且由于算法中使用了向量和矩阵运算来计算均值和协方差，因此不需计算Jacobian矩阵，运算速度更快.

假设状态向量x(n维)选取2n+1个采样点xi，i=0，…，2n ，.Sigma 点的采样规则如下:

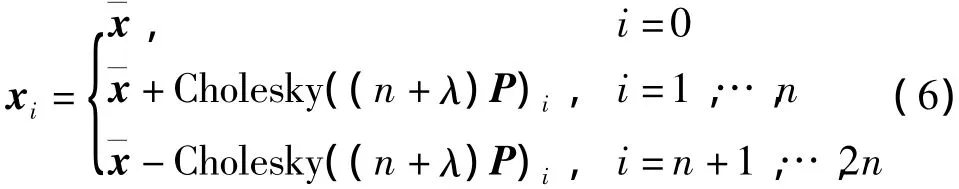
则x(k)的均值和协方差矩阵可以近似为

其中，矩阵Cholesky((n+λ)P)i是矩阵(n+λ)P经过Cholesky分解得到的第i行或第i列向量.λ=α2(n+κ)－n为尺度因子，α为尺度参数，决定Sigma点的分布范围.α、β、κ取值范围为0≤α≤1，β＞0，κ通常取0或(3－n).

3 主要结论

本节采用特征建模的思想，在原来复杂的动力学模型的基础上建立特征模型，从而使得控制器和滤波器的设计大大简化;采用CSUKF估计特征模型的参数，并对测量输出进行滤波，通过在线调整观测器误差的协方差矩阵，使算法具有更好的自适应性.

3.1 基于特征模型的滤波模型

在对高超声速飞行器动力学模型进行特征建模后，将式(2)中的二阶差分方程和其输出方程联立

式中v(k)为测量噪声.

将该特征模型化成状态空间的形式:

其中:

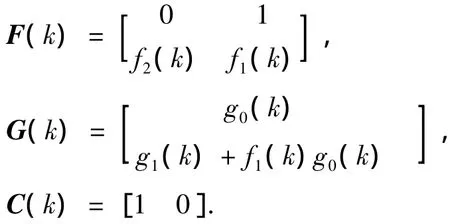
式中，X(k)=［x1(k)，x2(k)］T;w(k)为参数辨识偏差引起的状态误差，(k)为测量噪声引起的测量误差.在系统稳态阶段辨识参数与真实系统输入输出等价的前提下，将w(k)(k)视为白噪声，Γ是适当维数的已知矩阵.

将式(11)中的状态方程进行离散化

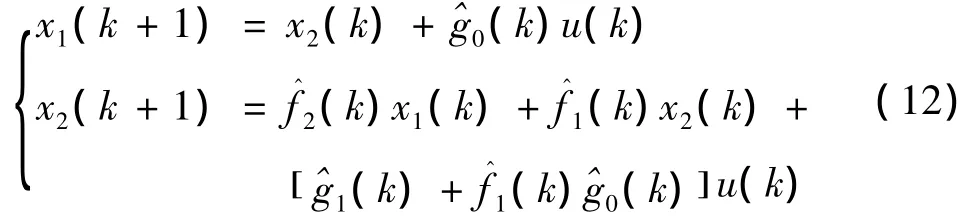
该模型只是一个近似模型，体现了STF的状态与参数的联合估计的思想［12］.在未知参数变化规律的情况下，采用此模型作为强跟踪的模型.

离散化状态方程和输出方程的具体表示为

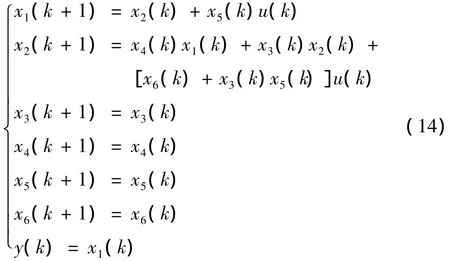
3.2 CSUKF

在式(14)中建立了基于特征模型的滤波模型，针对该模型设计滤波算法，通过STF的多重渐消因子在线调整UKF观测器误差的协方差矩阵，使算法具有更好的自适应性.该算法的具体步骤如下:

(1)系统状态初始化

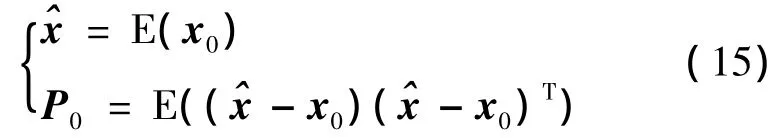
对于i=0，…，2n，计算UKF算法中的Sigma点.

(2)时间更新

系统的状态变量通过UKF计算，由STF计算得到多重渐消因子Λ，在线调整协方差矩阵.

其中，

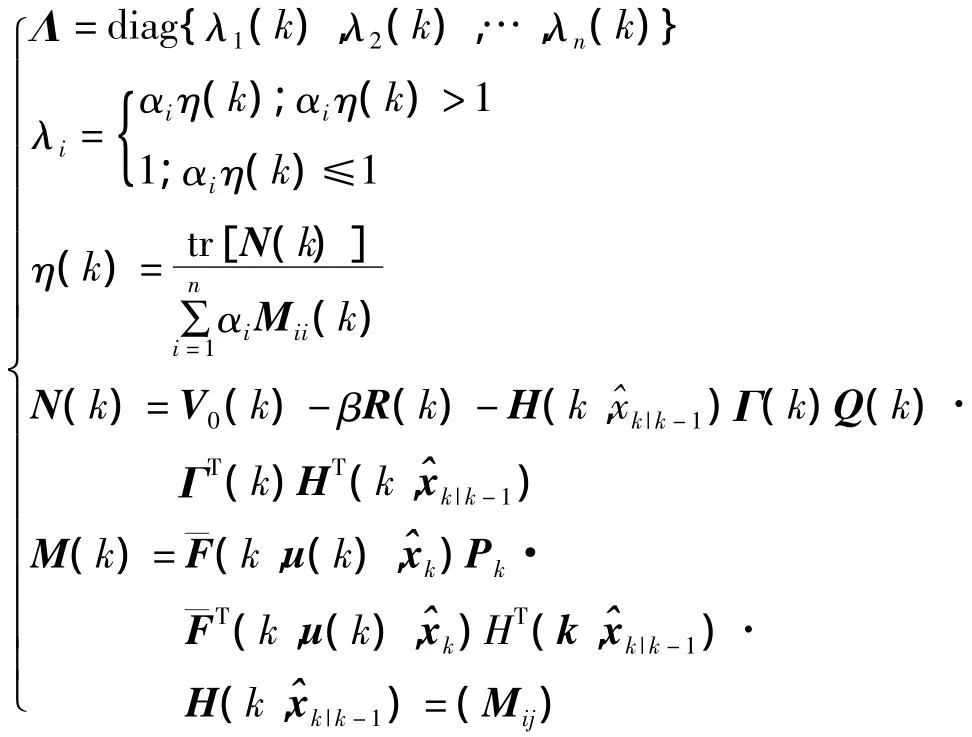
各参数的物理意义参见文献［12］.

(3)测量更新

通过调整多种渐消因子矩阵可以达到调整滤波增益K而提高估计精度的目的，从而提高改算法的鲁棒性和自适应性.

5 仿真验证

高超声速飞行器高空无动力滑翔段姿态控制器的任务可以简化为使其跟踪一定的攻角及滚动角指令，保持侧滑角在零附近.采用式(1)对飞行器进行单通道特征建模，验证控制器性能，根据一组类X-20构型飞行器气动特性的数值计算结果得到仿真的气动模型，并通过线性插值得到稀薄气体特性下的气动力矩系数.再入初始条件为飞行器初始高度62km，经纬度均为零度，速度方向指向东.初始姿态俯仰角0°，偏航角90°(与正北方向夹角，90°表示弹体指向东)，滚动角 0°.速度大小 6km/s(约为19Ma)，攻角 0°，侧滑角 0°.舵偏角初始状态均为0°，飞行器初始角速度为0(°)/s.整个飞行过程攻角跟踪10°，侧滑滚动角均跟踪0°.

3个通道的测量噪声均为符合N(0，0.1)分布的白噪声.飞行时间为1000s，采样时间为0.01s.整个飞行过程中，飞行高度从62km降到约33km，飞行速度从6km/s降到约2km/s，气动特性大范围变化.

系统的控制回路设计如图1所示.

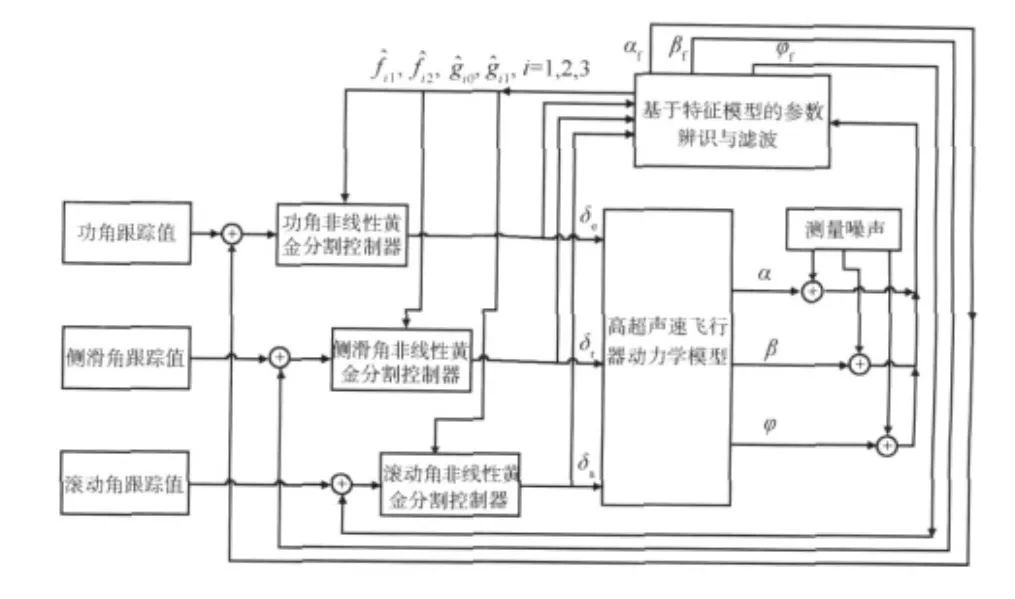
图1 高超声速飞行器姿态控制回路

由图1的控制回路可以看出，参数辨识与滤波是在闭环条件下进行的，控制是在辨识的基础上实施，二者相互交替影响.此处的滤波器一方面辨识得到黄金分割控制器的参数，另一方面对测量输出信号进行滤波，显然，此闭环辨识的目的是为了获取更优的控制器参数，并结合滤波算法对噪声进行抑制，从而得到更好的跟踪输出.仿真实验在保持控制器参数不变的情况下在无滤波，CEKF，CUKF和CSUKF 4种情况下进行.仅以攻角通道为例，对其仿真结果进行比较，其中，仿真时间为1000s，采样时间为0.01s，4组实验控制器的初始给定参数相同，实验在稳态阶段(15～1000s)的控制量、系统输出以及滤波输出的均值、方差如表1所示.仿真曲线如图2～8所示.

表1 稳态跟踪均方根误差

仿真曲线和表1表明基于特征模型的非线性黄金分割控制器对高超声速飞行器这一类大范围时变参数的非线性不确定性系统具有较好的鲁棒性和适应性，在未施加滤波的情况下仍然可以得到稳定的输出，且具有较高的系统输出精度.比较图2的4组曲线，未施加滤波的系统稳态控制量的振幅非常大，这样将导致舵面的剧烈抖动，这对于高超声速飞行器的控制是非常不利的.而黄金分割控制器的控制量是根据估计参数和测量值进行计算的，如果没有在线滤波，噪声引起的参数估计和测量值的偏差必然导致控制量的抖动.结合图3的过渡过程控制量输出曲线，CEKF和CUKF在过渡过程均出现了一定的振荡，而CSUKF过渡过程最平稳，稳态过程的控制量输出均方根误差最小，对控制作用的改善最为明显.

由图4的系统输出比较可以看出，加入滤波之后，稳态性能有了一定改善.CSUKF的稳态性能改善最为明显，图5也表明其稳态滤波精度最高.实际上对于全系数自适应控制回路，由于无法做到充分激励而造成的辨识偏差造成了特征建模和模型与实际系统之间不匹配，再加上噪声特性的不确定，强跟踪滤波使这些模型不确定性通过调整残差序列的正交优化滤波增益，在线调整UKF采样点，抑制不确定噪声的影响，从而使其比CEKF和CUKF具有更强的鲁棒性和跟踪能力.

图6给出了过渡过程(0～15s)3种滤波方案系统输出和滤波估计的对比，可以看出CSUKF的动态性能要优于前两者，但CEKF和CUKF也可以获得较理想的动态性能，由于闭环回路的反馈修正作用，虽然没有多重渐消因子来优化滤波增益，但可以通过偏差自动调节非线性黄金分割自适应控制器的参数进而优化动态输出，显然，此处的滤波与控制是互相作用互相影响的，仿真实验说明基于特征模型的滤波算法具有较高的鲁棒性.

图8 飞行过程速度变化曲线

图7和图8为飞行器飞行过程的高度和速度变化曲线.

综合以上仿真结果，在飞行环境大范围变化过程中，CSUKF与非线性黄金分割自适应控制律相结合可以保持姿态角的跟踪性能，有效改善控制的平稳性，且具有更好的滤波精度和系统输出，从而能更好的处理含测量噪声情况下的高超声速飞行器的辨识与控制问题.

5 结论

本文采用特征模型的思想处理高超声速飞行器这一复杂的非线性不确定系统，无需知道系统的确切模型，使滤波和辨识模型大大简化;将强跟踪滤波和无迹卡尔曼滤波相结合，应用于含测量噪声的高超声速飞行器基于特征模型的在线估计问题，并在此基础上通过非线性黄金分割控制器对恒定的攻角、侧滑角和滚动角度进行跟踪，仿真结果表明，CSUKF算法可以有效的进行噪声抑制和参数的在线辨识，与基于特征模型的非线性黄金分割控制律组成控制回路可以较好的实现测量噪声下的姿态角的跟踪性能，具有很好的鲁棒性.从计算量来说，CSUKF略大一些，但也是适中的，可作实时算法，在线应用.

［1］ Xu H J，Ioannou P A.Adaptive sliding mode control design for a hypersonic flight vehicle［R］.Catt Technical Report，No.02-02-01，2002

［2］ Harald B，Anthony J C.Robust control of hypersonic vehicles considering propulsive and aeroelastic effects［C］.AIAA Guidance Navigation and Control Conference，Monterery，CA，August 1993

［3］ Gao D X，Sun Z Q，Du T R.Dynamic surface control for hypersonic aircraft using fuzzy logic system［C］.The IEEE International Conference on Automation and Logistics，Jinan，China，2007

［4］ Xu H J，Mirmirani M，Ioannou P A.Robust neural adaptive control of a hypersonic aircraft［C］.AIAA Guidance，Navigation，and Control Conference and Exhibit，Austin，Texas，USA，2003

［5］ 吴宏鑫，胡军，解永春.基于特征模型的智能自适应控制［M］.北京:中国科学技术出版社，2009

［6］ 孟斌，吴宏鑫.基于特征模型的X-34爬升控制研究［J］.中国科学 F辑，2009，39(11):1202-1209

［7］ 龚宇莲，吴宏鑫.高超声速飞行器基于特征模型的自适应姿态控制［J］.宇航学报，2010，31(9):2122-2129

［8］ Irene M G，Rajiv S C，McMinn JD，et al.Hypersonic vehicle model and control law development using H∞and μ synthesis［J］.NASA Technical Memorandum 4562，1994

［9］ 王丽娇.基于特征模型的高阶线性不稳定系统的参数辨识与控制［J］.空间控制技术与应用，2010，36(5):25-31

［10］ Kim C，Sakthivel R，Chung W K.Unscented fast SLAM:a robust and efficient solution to the SLAM problem［J］.IEEE Transactions on Robotics，2008，24(4):808-820

［11］ Shojaie K，Shahri A M.Iterated unscented SLAM algorithm for navigation of an autonomous mobile robot［C］.IEEE/RSJ International Conference on Intelligent Robots and Systems，NJ，USA，2008

［12］ 周东华.非线性系统的自适应控制导论［M］.北京:清华大学出版社，2002