基于遗传算法的均衡交通分配研究
2011-04-17夏小棠李庭洋
夏小棠,李庭洋
(1.武汉科技大学城市设计学院,湖北武汉430081;2.武汉城市职业学院,湖北武汉430064)
1 引言
在城市及区域交通规划中,交通分配作为一个重要环节起了关键的作用。随着人工智能、数学规划等方法的发展,对交通分配模型的研究与应用也日趋成熟。国际上按照wordd rop提出的第1和第2原则,将交通分配模型划分为均衡模型和非均衡模型[1]。均衡交通分配理论在近几年发展较快,与非均衡交通分配模型相比,这类模型具有思路明确、结构严谨、结果合理、有利于宏观研究等优点。
近几年,对均衡分配问题的求解出现许多新的算法,虽然这些算法的运算复杂度在一定程度上降低了,但处理大规模复杂的交通网络问题仍比较困难。这都迫切需要一种新的算法使之能建立易于编程的、计算能力快的、更贴近实际交通状况的预测模型。因此,本文尝试将易于计算机编程,且具有全局搜索功能以及并行运算特点的遗传算法应用于求解均衡交通分配模型。
2 遗传算法的一般理论
遗传算法(Genetic A lgorithm)是一种模拟生物在自然界环境中遗传和进化过程而形成的一种全新的全局搜索和优化方法。它从任一初始群体出发,通过随机选择、交叉和变异等遗传算子,使种群一代代进行到空间中最好的区域,直至达到最优点。其主要特点包括直接对结构对象进行操作,不要求函数连续性以及求导;全局寻优能力更强;有内在的并行性。遗传算法已成为当今影响最广泛的进化方法之一,是现代有关智能计算问题中的关键技术,被人们广泛地应用于不同的领域,如信号处理、自适应控制、组合优化、人工生命和机器学习。
2.1 编码
编码实际上就是从解空间把问题的可行解转换到遗传算法的搜索空间。编码一般有3种方式,即符号编码方式、浮点数编码方式以及二进制编码方式。二进制编码方式中,每个自变量用s位二进制的子串表示,n个问题用s×n表达,假设 的取值范围在xi min~xi max,则编码的区间为[0,2s]。
2.2 遗传操作
2.2.1 选择
选择就是以适应度高的个体为依据,从群体中把父个体选择出来,并令其产生相应的后代,淘汰适应度低的个体。常用的选择方法主要有以下几种:比例的变换,竞争的选择,轮盘赌的选择,稳态复制,排序,共享等。Holland提出的轮盘赌选择法(roulettew heel selection)是诸多选择方法中最有名、最常用的方法。
2.2.2 交叉
交叉是依照交叉概率,将种群中的2个能够相互配对的父个体的部分结构按照某种特定的方式替换和重组形成2个新的个体。交叉的方法可以根据编码方法不同而变化,例如二进制编码进行的二进制交叉,实值编码进行的实值交叉等。在二进制交叉中又可以分为均匀交叉、单点交叉以及多点交叉。实值交叉通常有中间交叉、离散交叉、算术交叉等。
2.2.3 变异
变异是根据某一个很小的概率随机地改变群体中个体的某些基因。依据个体编码表示方法的不同,变异方法也不同,如二进制编码中的1变成0,0变成1。变异算法有2个重要作用,包括使遗传算法具有较强的局部随机搜索能力;使遗传算法能维持群体多样性,防止未成熟收敛的现象出现。
2.3 终止条件
算法终止,即最优个体的适应度达到设定的阀值;最优个体的适应度以及群体适应度不再变化时;迭代次数达到预先设定的次数。
2.4 遗传算法在约束优化问题上的处理方法
遗传算法用于约束优化问题的求解常用的有几种方法,包括可行域、混合法、算子修正法、罚函数法[2]。采用线性约束的等式消除某些变量,用其他的线性组合代替变量,并修改线性不等式;采用专门设计的修正算子,对不可行染色体进行修复,保证后代一直是可行的;采用罚函数法,通过惩罚不可行解将有约束的问题转化为无约束的问题,使得遗传算法可以在可行域和不可行域中搜索到最优解。
3 基于遗传算法的用户均衡分配模型
3.1 用户均衡模型
交通分配就是将OD矩阵q中的交通需求量安排到路网中,从而形成路段流量 x,该过程按照Wardrop第一原则(UE原则)进行,用求解数学规划的问题算出符合UE条件的流量分布,公式如下:
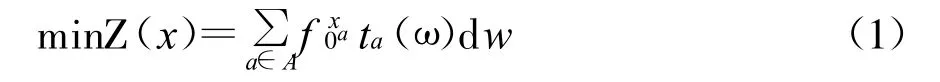
约束条件:
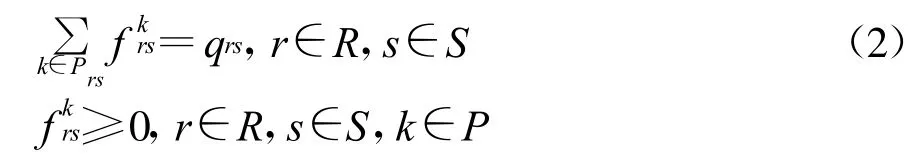
路段流量由公式计算:
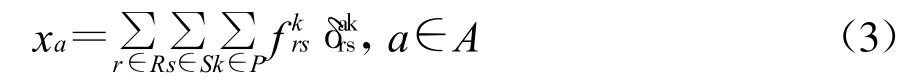
其中,路段时间函数被假定成路段交通流量的单调、连续上升函数,只与自身的路段流量有关。目标函数是路段时间函数的积分。约束条件令每个OD对之间所有路径流量的和等于相应的OD需求,约束条件描述了路径流与路段流之间的关系。
3.2 模型的设计
3.2.1 算例
某一简化的交通网络见图1。
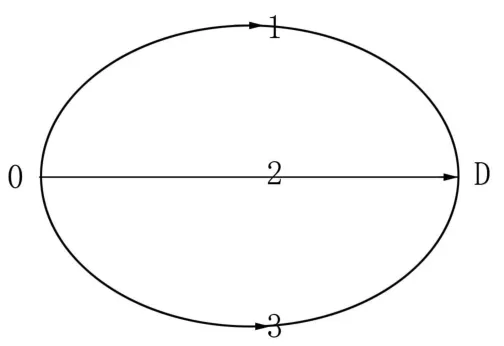
图1 交通网络图
其中,OD量为300,3个路段的时间阻抗函数为:
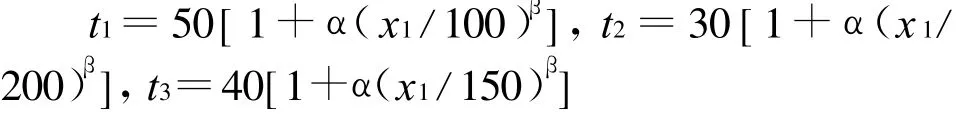
α、β是调教系数,建议 α=0.15,β=4。
3.2.2 模型分析及求解过程
该交通网络的用户均衡,交通分配问题可以表示成数学规划模型。
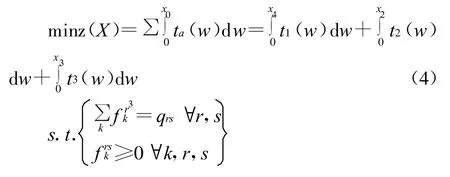
其中ta为路段的阻抗函数,a=1,2,3;qrs为OD流量为r、s间第k条路段的流量,即将OD流量qrs、路阻函数 ta带入优化模型,得到公式如下:

采用罚函数法将目标函数转换成增广目标函数p(X,u),公式如下:
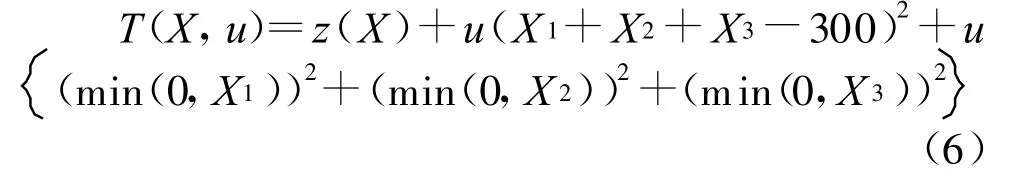
式中 T(X,u)为增广目标函数;z(X)同上;u为惩罚因子,且 u>0,当 u→∞时,目标函数逼近最优解。通过遗传算法求解。
(1)可行解采用二进制编码,每个自变量的取值范围在[0,300],用8位二进制数表示,染色体串的长度为8×3=24。
(2)个体适应度函数:
F(X)=1/z(X) (7)
(3)解码方法:
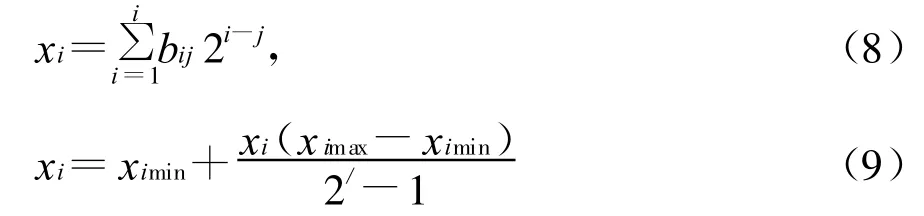
得到结果:x1=0+xi(300-0)/(28-1)。
(4)遗传算子为比例遗传算子,种群适应度之和F的计算公式如下:

对染色体选择的概率计算使用公式如下:
pi,pi=F(Xi)/F,i=1,2,…,popsize
对染色体累加的概率计算使用公式如下:
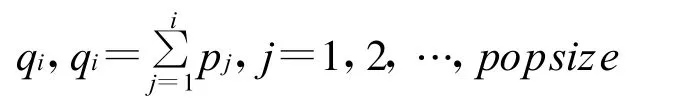
对于产生一个位于[0,1]区间的长度为popsize随机数的序列,其中的任意的一个数r若满足qi-1<r<qi,则选第 i染色体(i=1,2,…,popsize),这样就得到新的种群。运算交叉,单点交叉算子;运算变异,基本位变异算子。遗传算法的运行参数。设定群体的规模(popsize)为100,交叉概率为0.95,变异概率为0.001。经过计算,得到结果如下:X1=118.309 2,X2=122.535 3,X 3=59.154 6;t1=40.154 1,t2=40.145,t3=40.1451最优值:z(X)=11 028.385。从最后的运行结果可知,所有路径的交通时间趋于相等,即t1=t2=t3=40.145 1,系统朝着均衡方向发展,整个路网达到用户最优状态。
4 结语
从实例分析可见采用遗传算法解决用户最优的均衡交通分配模型是可行的。由于遗传算法模型简单,易于计算机编程且求解速度快,对函数的可微性或连续行等没有要求,只要所要求解的问题的目标函数是可计算的便可,在计算机的帮助下,可灵活的处理许多交通网络问题,方便了使用者的具体操作。
[1]陆化普,黄海军.交通规划理论研究前沿[M].北京:清华大学出版社,2007.
[2]玄光男,程润伟.遗传算法与工程优化[M].北京:清华大学出版社,2006.
[3]姜友华,王新生.遗传算法用于产生可供选择的城市规划方案[J].武汉大学学报,2002,35(3),63~65.
[4]雷英杰,张善文,李续文,等.M ATLAB遗传算法工具箱及应用[M].西安:西安电子科技大学出版社,2005.
[5]Booker,Goldberg L B,Holland J H.Classififier Systems and Genetic A lgo rithm s[J].A rtificial In telligence,1989(40):235~280.
[6]Feng C,Lin J.Using a genetic algorithm to generative sketch m aps for u rban planning[J].Com puters Environment and Urban system,199,23(2):92~ 100.
[7]Richad JB,John T T,M ichael R B.M ultiobjective u rban p lanning using genetic A lgorithm[J].Jou rnalof U rban and Development,1999,125(2):86~ 99.
