规划态中压配网供电可靠性评估模型①

李历波，王玉瑾，王主丁，叶 云，李旭前

（1.重庆市电力公司綦南供电局，重庆401420；2.重庆大学输配电装备及系统安全与新技术国家重点实验室，重庆400044；3.玉溪供电局，玉溪653100）

配电网供电可靠性是度量配电网在某一定时期内，能够保持对用户连续充足供电的能力的程度。配电网供电可靠性的评估主要是包括可靠性指标的统计分析评价和可靠性的预测评估两方面。可靠性指标的统计分析是对现状网的可靠性分析，是配电网规划的依据。但是，要从根本上改善配电网的供电可靠性，就必须在配电网的设计规划阶段对可靠性进行预测评估。

根据供电可靠性的定义，提高配电网的供电可靠性，必须尽可能减少用户每年的停电次数和每次停电的时间。目前，相比中压配电网，城市高压和低压配电网的供电可靠性很高，对供电可靠率指标的影响相对不大。因此，对城市中压配网供电可靠率计算分析是配网规划中可靠性评估的重要部分。

目前，工程上普遍应用的配电网可靠性计算方法主要有故障模式影响分析法，最小路集法和最小割集法，人工神经网络法，可靠性框图法和故障树分析法等，但由于大多数算法要求已知网络详细数据，故难以在实际电网规划中使用。

基于故障模式后果分析法，从配电网规划中可靠性预测评估的实际应用角度出发，提出了一种在中压配电网规划中的可靠性评估的简化模型，以及一种基于对现有可靠性数据的修正模型。

1 基于故障模式后果分析法的可靠性评估

故障模式后果分析法的基本思想是，通过故障枚举法首先选择一个故障状态，对该故障引起的系统状态改变进行分析，进而找出受影响的线路及停电的负荷点，最后计算该状态对可靠性指标的影响。一般情况下，系统故障停运状态选择是按某种逻辑逐个地选择，例如可以首先检验所有单重偶发事故，继而是双重偶发事故，直至所有状态检验完毕。但是在中压配网规划中，规划年负荷和线路的详细数据是难以预知的，因此，规划中可靠性计算只能建立在简化并实用的评估模型上。在评估模型上，可靠性计算一般只考虑单重事故的影响。

城市中压线路主要采用环网接线、开环运行的结构，线路互倒互带能力较强，但部分郊区与农村线路仍然为单辐射线路。在线路上装设的分段开关，可将每条线路分为若干区段，则停电时不再是停整条线路的负荷，而是只停相关区段负荷，这样减少每次停电的用户数，从而用户每年的平均停电时间也减少了。

图1所示的是一个简单常开环网的典型接线，正常运行时，分段开关1，2，3，4，5中至少有一个处于断开状态（如图中开关3），一般称为联络开关。常开环网正常运行时联络开关的两侧都相当于一条馈线的末端，当某侧电源停电时，可自动或通过人工操作闭合联络开关，由另一侧反向送电，受影响但可隔离的非故障段只是感受到故障的巡查时间（巡查时间包括故障隔离和非故障段供电恢复时间）。假设分段开关两侧都装有隔离刀闸，当故障发生在分段开关时，开关修复时间不影响用户用电，只有故障的巡查时间会造成用户的电能损失。对于单辐射线路，由于不存在负荷转带的可能，所有受故障或计划检修影响的元件都要感受到故障修复或计划检修时间。

图1 简单常开环网Fig.1 Simple open－loop network

2 中压配电网规划可靠性评估

2.1 中压配网规划可靠性指标

中压配电网的可靠性指标，分为主要指标和参考指标两大类：主要指标有用户平均停电时间，供电可靠率，用户平均停电次数，用户平均故障停电次数，用户平均预安排停电次数，系统停电等效小时数，参考指标有用户平均预安排停电时间，用户平均故障停电时间，平均停电用户数等。

考虑到可靠性评价指标众多和规划态可靠性评估的简化，本文可靠性评估仅对主要指标中的用户平均停电时间和供电可靠率进行估算。供电可靠率RS－1和用户平均停电时间Tavg的关系可表示为

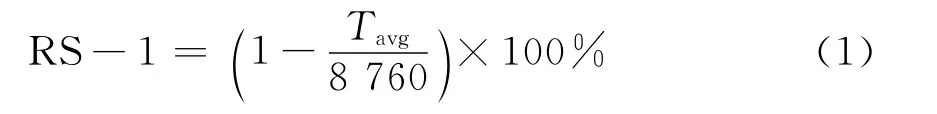
2.2 中压配电网规划可靠性评估的总体思路

本文总体思路是将规模庞大的配电网可靠性计算等效为若干典型接线模式的可靠性指标计算的加权平均，从而使得规划中可靠性评估这一复杂问题得以简化，并且具有实用性。具体算法主要描述为以下几个步骤：

1）由于规划阶段中压配网支线难于确定，因此，仅考虑规划网主干线的可靠率计算；并根据配电网开关有无选择性，分段和联络情况的不同，将配网络结构抽象为几种典型接线方式。

2）综合考虑各项主要影响因素，计算各种典型接线模式用户平均停电时间。

3）根据各典型接线间比例，将规划网用户平均停电时间加权平均后求得全网的用户平均停电时间，最终求得全网的供电可靠率。

3 规划态中压配网用户平均停电时间估算

由式（1）可知，若已知用户平均停电时间Tavg，供电可靠率RS－1即可得到。下面仅对用户平均停电时间估算方法进行讨论。

3.1 简化估算模型

在规划网络中，设第i条主干线的长度为Li，分段数为Ni，各区段长度和用户相同，单条馈线上两段同时故障的概率为零，只考虑单条馈线发生故障或检修的情况，并且有联络线路故障或检修后负荷转带能力为100%。

用户的平均停电时间在不同接线方式的网络中有不同的计算方法，先分别就有联络开关有无选择性，以及单辐射线路开关有无选择性四种情况估算单条馈线用户的平均停电时间；再以各线路长度为权重进行加权平均，得到整个配网的用户平均停电时间。

3.1.1 有联络线路用户平均停电时间估算

有联络线路i再分两种情况估算线路用户的平均停电时间Ti，sd1为Ti，sd2。

1）馈线开关有选择性

馈线开关有选择性即是发生故障时离故障点最近的上游开关先跳闸，此时用户的平均停电时间可表示为

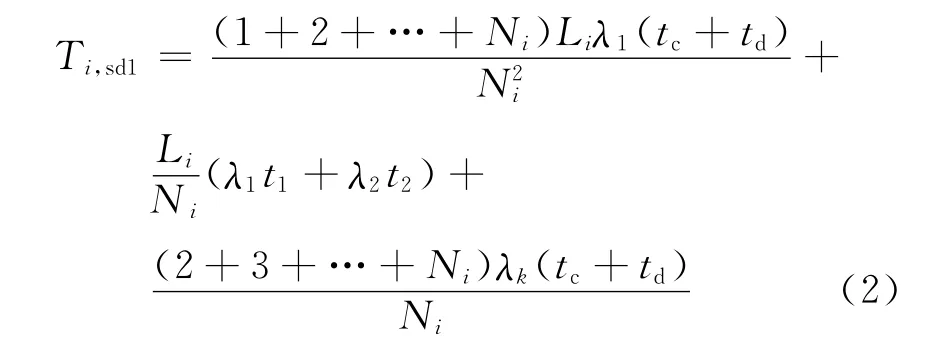
其中λ1为架空线路／电缆故障率，单位为次／（年·km）；λ2为架空线路／电缆检修率，单位为次／（年·km）；λk为开关故障率，次／（台·年）；t1为架空线路／电缆故障平均修复时间，单位为h；tc为架空线路／电缆检修平均修复时间，h；tc为架空线路／电缆故障巡查时间，h；td为故障后倒闸操作时间。

2）馈线开关无选择性

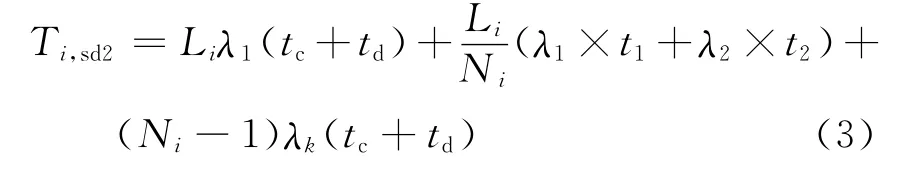
3.1.2 单辐射线路用户平均停电时间估算

单辐射线路i再分两种情况估算线路用户的平均停电时间Ti，df1为Ti，df2。

1）馈线开关有选择性

馈线开关无选择性即是发生故障时总在馈线首端跳闸，此时用户的平均停电时间可表示为

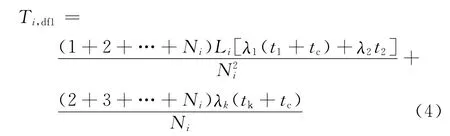
其中tk为开关故障平均修复时间，单位为h。

2）馈线开关无选择性

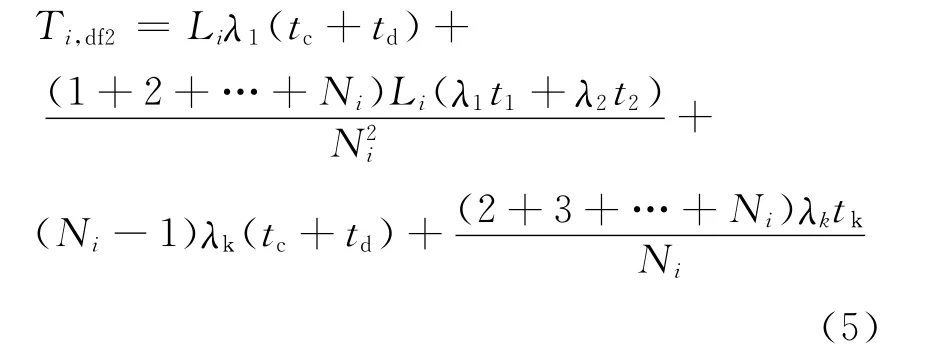
3.1.3 中压配网用户平均停电时间估算

在各规划年，通过对各高压变电站供区内中压线路新增及改造规划，可知各变电站中压出线回路数、主干线长度及其分段和联络信息。设对应于Ti，sd1、Ti，sd2、Ti，df1和Ti，df2的馈线集合分别为Msd1、Msd2、Mdf1和Mdf1，则整个配网或某分区用户的平均停电时间Tavg可表示为

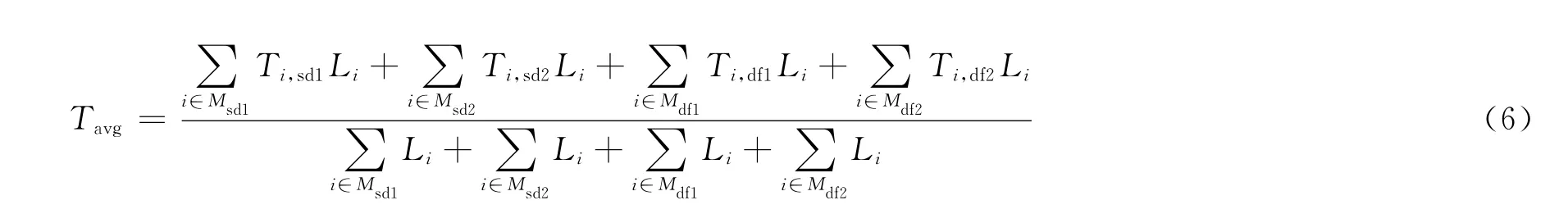
例如，按照上述方法，可分别计算出规划后两种接线方式下（单幅射和有联络）用户平均停电时间，并以各自线路主干线总长度作为权重，可得规划网用户平均停电时间为

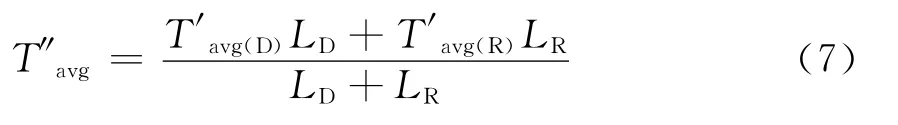
其中T′avg（D）和LD分别为规划后单幅射线路用户平均停电时间及主干线总长度；T′avg（R）和LR分别为规划后有联络线路用户平均停电时间以及主干线总长度。

3.2 修正估算模型

通过对上述模型的分析和用户平均停电时间计算的推算，可以发现，用户平均停电时间主要受三部分影响，分别为故障巡查、故障检修和计划检修。若忽略故障率相对很低的开关故障影响，则影响中压配网用户平均停电时间的三部分可分别与相关参数成正比，详见表1。在该表中，联络分段因子用以考虑馈线分段和联络情况的不同。根据配电网供电的特点，将基本网络结构抽象为若干典型接线方式。采用故障模式后果分析法，可得到中压电网典型接线方式的停电时户数相对比例数，即联络分段因子，如表2所示。

表1 影响用户平均停电时间的主要参数Tab.1 Main parameters related to customer average interruption time

表2 各接线方式的联络分段因子Tab.2 Linkage factors of various network configurations

若已知现有用户平均停电时间，经规划网主干线长度、线路计划检修率和检修时间、联络分段因子成比例修正后，可得规划网用户平均停电时间为

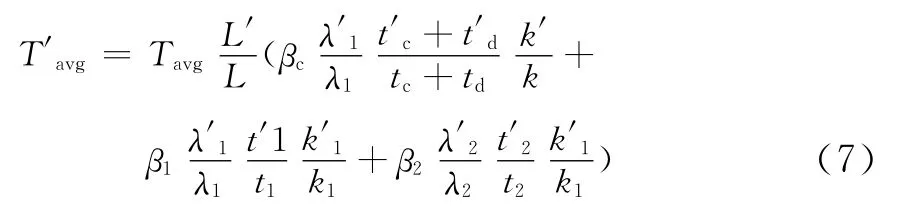
其中：Tavg和T′avg分别为规划前和规划后的用户平均停电时间；L、L′分别为规划前、后主干线平均馈线长度；λ1、λ′1分别为规划前、后线路故障率；λ2、λ′2分别为规划前、后线路计划检修率；tc、t′c分别为规划前、后线路故障巡查时间；td、t′d分别为规划前、后线路故障后倒闸操作时间；t1、t′1分别为规划前、后线路故障检修时间；t2、t′2分别为规划前、后线路计划检修时间；k、k′分别为规划前、后故障巡查联络分段因子；k1、k′1分别为规划前、后故障检修／计划检修联络分段因子；βc、β1和β2分别为线路故障巡查，线路故障检修和线路计划检修影响用户停电时间比例因子（βc＋β1＋β2＝1）。

由于式（7）中包含了现状年实际的用户平均停电时间，在一定程度上可自动考虑某些变化不大的复杂因素（如气候）。

4 实例分析

本文提出的模型和方法已在云南贵州等省的县级电网规划的可靠性评估中得以运用。现以某城区为例，根据其配电网特点，分别运用上文的规划态简化估算模型和修正估算模型进行分年度供电可靠性理论计算。

4.1 计算条件

参照实际统计资料并结合规划态网架及线路的各项指标，采用表3的计算条件。

4.2 计算结果分析

运用规划态可靠性简化估算模型和修正估算模型对表3的计算条件进行可靠性理论计算，结果如表4所示。从表4可以看出，运用两种估算模型得到的估算结果相近，规划网供电半径、线路分段、环网率各年度的优化程度及其它因素对可靠性的影响均被定量反映出来，可以清楚看到用户平均停电小时数的减少量和供电可靠率的提升量，从而可以检测规划态中压配网是否满足设计要求。运用两种模型的计算结果又有一定的差别，这是由于，第一种方法考虑了更全面的影响因素，通过规划态各种影响因素的具体数值计算得到，而第二种方法较第一种方法忽略了次要的影响因素，是基于现状网可靠性数据的一种修正方法。该方法以现状网可靠性数据为依据，提高了规划态评估结果的可信度。该方法可以不需要知道各因素的具体数值，只需知道反映各主要参数变化的比例因子，并且该方法可实现某几个因素的单独评估。

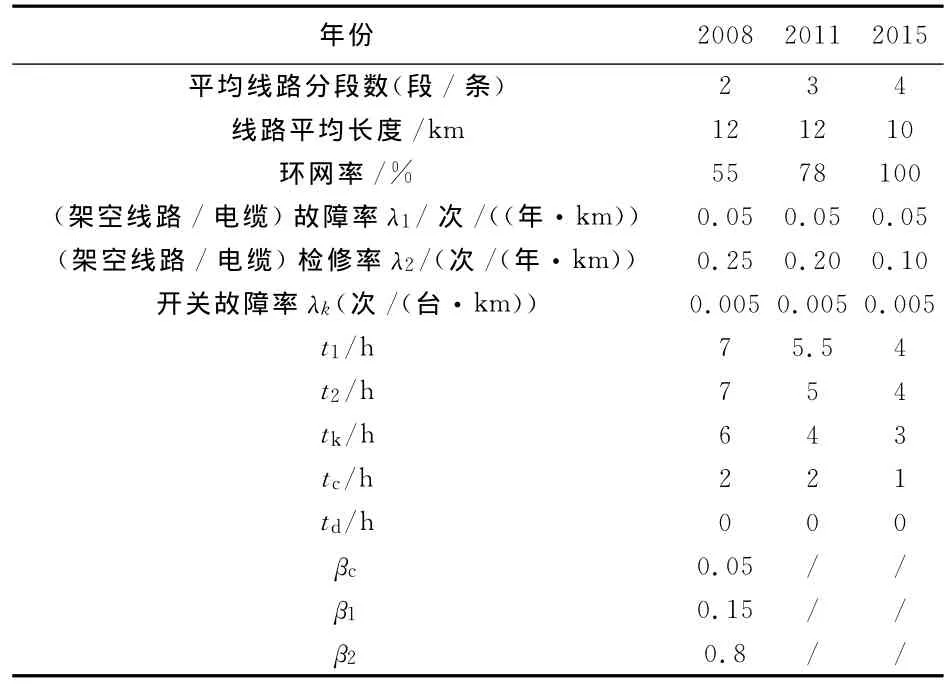
表3 某城区供电可靠性估算条件Tab.3 Reliability evaluation parameters of some city urban areas

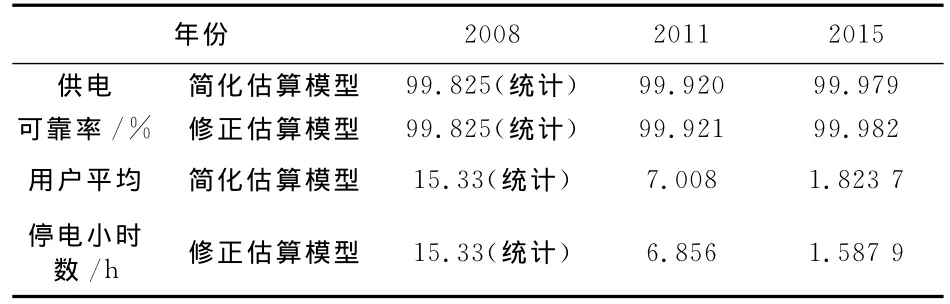
表4 某城区可靠性指标理论计算结果Tab.4 Reliaility evaluation results of some city urban areas

5 结语

本文提出了适用于中压配网规划网架可靠性评估的简化估算模型和修正估算模型。两种模型都不需要详细的网架数据，特别是修正估算模型，为判断规划方案是否达到可靠性指标提供了定量的参考依据。目前，所提模型和方法已在云南和贵州多个县级电网规划中得到应用，实现了电网规划中可靠性的定量估计。

［1］ 方向晖.中低压配电网规划与设计基础［M］.北京：中国水利水电出版社，2004.

［2］ 姚李孝，赵兵，伍利，等（Yao Lixiao，Zhao Bing，Wu Li，et al）.基于混合算法的复杂配电系统可靠性评估（Hybrid method for the reliability evaluation of complex power distribution system）［J］.电力系统及其自动化学报（Proceedings of the CSU－EPSA），2006，18（6）：96－102.

［3］ 汪穗峰，张勇军，任倩，等（Wang Suifeng，Zhang Yongjun，Ren Qian，et al）.配电网可靠性定量分析研究综述（An overview of quantitative analysis of distribution system reliability）［J］.继电器（Relay），2008，36（3）：79－83.

［4］ 邱生，张焰，徐洋，等（Qiu Sheng，Zhang Yan，Xu Yang，et al）.复杂配电网的供电可靠性定量评估（The quantitative evaluation of complex distribution system reliability）［J］.上海交通大学学报（Journal of Shanghai Jiaotong University），2005，39（12）：2079－2082，2087.

［5］ 雷娜，周渝慧，王蓉蓉（Lei Na，Zhou Yuhui，Wang Rongrong）.贝叶斯网络的复杂配电网可靠性评估（Reliability assessment of complex distribution network basing on Bayesian network）［J］.电力系统及其自动化学报（Proceedings of the CSU－EPSA），2009，21（1）：108－112.

［6］ 张红云，翟晓凡，吴晓蓉，等（Zhang Hongyun，Zhai Xiaofan，Wu Xiaorong，et al）.中压配电网可靠性理论计算及分析（Reliability evaluation and analysis of medium voltage electrical distribution networks）［J］.中国电力（Electric Power），2005，38（6）：28－32.

［7］ 李少华，韩富春（Li Shaohua，Han Fuchun）.一种配电系统可靠性评估新方法（A method of distribution system reliability evaluation）［J］.电力系统及其自动化学报（Proceedings of the CSU－EPSA），2002，14（6）：17－19.

［8］ 康庆平，卢锦玲，杨国旺（Kang Qingping，Lu Jinling，Yang Guowang）.确定城市10k V配电网线路最优分段数的一种方法（A method for optimizing the number of sections of feeder on 10kv distribution network）［J］.电力系统自动化（Automation of Electric Power Systems），2000，32（7）：57－59.

［9］ 王峻峰，周家启，谢开贵（Wang Junfeng，Zhou Jiaqi，Xie Kaigui）.中压配电网可靠性的模糊评估（Fuzzy reliability evaluation algorithm for medium voltage distribution networks）［J］.重庆大学学报：自然科学版（Journal of Chongqing University：Natural Science Edition），2006，29（2）：45－49.

［10］Billinton R，Wang P.Reliability－network－equivalent approach to distribution－system－reliability evaluation［J］.IEE Proceedings：Generation，Transmission and Distribution，1998，145（2）：149－153.

［11］李晓辉，徐晶，李达，等（Li Xiaohui，Xu Jing，Li Da，et al）.基于层次分析的配电网可靠性评估指标体系（Index system of reliability evaluation for distribution network based on analytic hierarchy process）［J］.电力系统及其自动化学报（Proceedings of the CSU－EPSA），2009，21（3）：69－74.