改进的遗传算法辨识综合负荷模型①

韩民晓，马 杰，姚蜀军，王 坤

（1.华北电力大学电气与电子工程学院，北京 102206；2.河南省电力公司郑州供电公司变电运行部，郑州 450006）

电力负荷作为能量的消耗者，在电力系统的设计、分析与控制中有着重要的影响。在进行电力系统分析时，不恰当地考虑负荷的模型，会使所得结果与系统实际情况不相一致，或偏乐观、或偏保守，从而构成系统的潜在危险或造成不必要的投资。负荷模型是影响动态仿真准确度和可信度的重要因素［1，2］。同时，在电力系统中的主要电气元件中，由于负荷的分散性、随机性和时变性，获得负荷模型具有很大难度。

实测负荷建模包含两个重要的方面：

（1）确定合适的负荷模型结构和形式；

（2）选择辨识算法进行参数辨识计算。

同时，这两个方面也是造成负荷模型分散性的原因。

文献［3］提出了一种综合负荷模型。该模型结构对现存的负荷机理式模型做一些相应的简化和改进，已经加入中国电科院的电力系统分析综合程序PSASP（power system analysis software package）中，是一种优秀的实用的负荷模型。

在确定合理的负荷模型结构后，选择具有全局搜索能力的优秀算法对克服模型参数的分散性具有重要意义。

遗传算法GA（genetic algorithm）作为一种有效的全局直接搜索方法，具有求解过程与梯度信息无关和将复杂的非线性问题经过有效搜索与动态演化转化到优化状态的特性，使得其应用于复杂问题的优化时具有很明显的优势［4］，因而在电力系统的诸多研究领域得到了广泛应用。

但基本GA存在易早熟和收敛速度慢的缺陷［5，6］，许多学者针对具体应用问题对其进行了一系列改进，如根据个体的适应度值自适应地改变交叉和变异概率，针对选择交叉和变异三个核心操作的改进，控制参数的改进等［7～10］。这些改进包括：（1）对选择算子的改进，如精英策略和随机－精英策略，能确保最优个体直接进入下一代，改善了遗传算法的选择效果，但存在不一定能将大部分优秀个体复制到子代的问题；（2）对交叉和变异算子的改进，根据个体平均适应度和最优适应度，设计种群的早熟指标，利用该指标自适应调整交叉和变异概率，能够根据个体的实际情况进行交叉和变异，改善了交叉和变异效果，但使用指数函数表示，待确定参数过多，稍嫌复杂。

本文针对负荷建模设计了比例选择策略和线性自适应交叉策略，试图以简单明了的方法，有效地改善遗传算法用于负荷模型辨识时的优化效果［6，11］。

1 综合负荷模型

综合负荷模型［3，12］采用三阶感应电动机并联负荷静特性的模型结构。如图1所示。其中，IM为感应电动机，属于动态部分；ZIP为负荷静态性。

感应电动机模型采用3阶机电暂态模型，采用的是电动机惯例，公式如下：

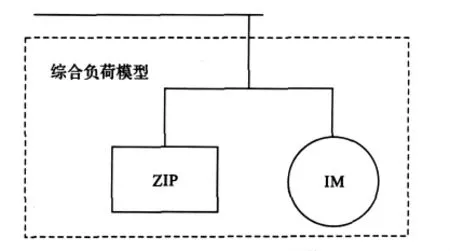
图1 TVA负荷模型结构Fig.1 Load model of TVA

其中

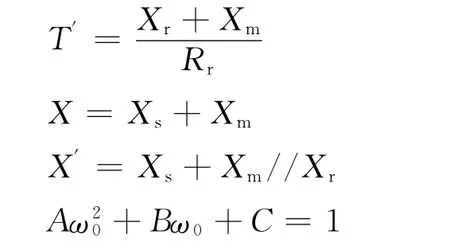
感应电动机待辨识的参数矩阵为［Rs，Xs，Xm，Rr，Xr，H，A，B］T，矩阵的8个元素都是电动机容量基值下的标么值，各个参数的含义见文献［3］。

静态部分采用负荷静特性ZIP模型结构，模型的公式如下：

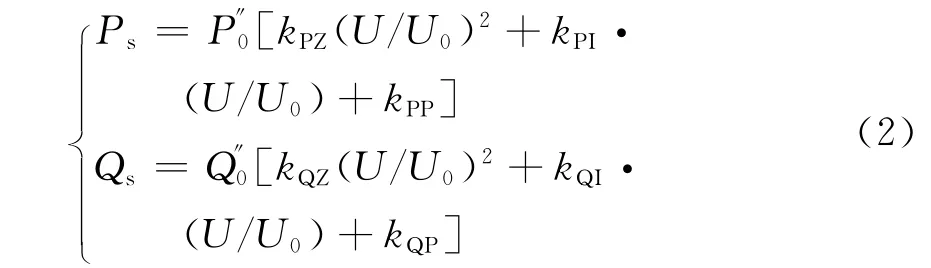
ZIP模型部分待辨识参数有4个，包括［kPP，kPZ，kQP，kQZ］T。除以上12个参数外，为将所有模型参数标么化还定义参数Kpm和Mlf。其中Kpm用来分配初始有功功率，Mlf为额定初始负荷率系数［3］。

设感应电动机的吸收的功率为Pim，Qim，综合负荷模型总的负荷特性为

2 改进的遗传算法

2.1 遗传算法的基本思想

GA是一种非线性优化方法，其基本思想是按一定规则生成基因编码初始群体，再从这些代表问题的可能潜在解的初始群体出发，挑选适应度强的个体进行交叉和变异，以期发现适应度更佳的个体，如此一代代地演化，直到得到一个最优个体，即对应问题的最优解或近似最优解。可见，GA涉及五大要素：初始种群设定、选择策略、变异策略、突变策略及适应度函数选择［5，6］。

2.2 比例选择策略

传统的选择策略有轮盘赌法，择优选择法及波尔兹曼选择策略等，还有一些改进的策略，如精英策略、随机－精英策略等。

本文设计的比例选择策略是根据各个个体的适应度占所有个体适应度之和的比例，确定每个个体被复制的个数，适应度大的个体复制的次数多。同时考虑到种群多样性问题，适应度小的个体也有可能被选中，其选中概率取决于被复制个体个数的小数部分。其操作过程为：

（1）求每代中各个个体的适应度之和，用适应度之和去除各个个体的适应度，进而求出各个个体的适应度和每个个体理论上被复制的次数Numi。

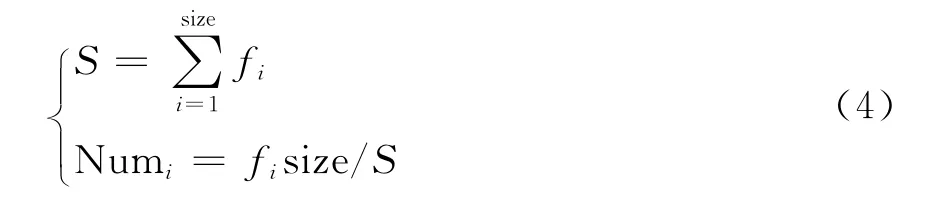
其中fi为每个个体的适应度，size为种群个体的个数，Numi为理论上每个个体应该被复制的次数，i＝1，2，…，size。

2）对Numi取整，得到每个个体应该复制的个数Ni，计算size个Ni之和与Numi的差。设Numi与Ni之差为resti，对resti排序，选择较大的r个resti对应的个体，使这r个个体的复制次数加1。式（11）中int表示取整。

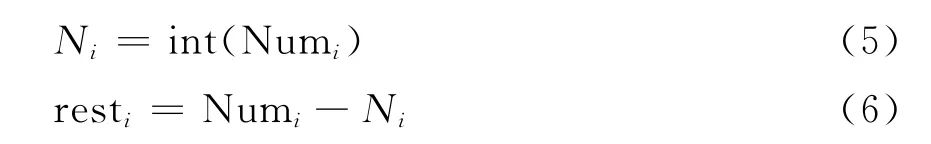
由于适应度较大个体的理论复制次数的小数部分不一定大，而一些适应度较小个体的理论复制次数的小数部分可能较大，这样，就有可能选择适应度较小的个体进入下一代，以增加种群的多样性。当然，适应度较小的个体被选择的概率是比较低的。

在完成项目建设之后投入到实际运营当中，所产生的养护费用，维修费用以及拆除费用都会影响项目成本。若仅仅降低施工成本，将会影响工程建设质量。同时也会提升后期维护费用，增加项目成本。因此，工程项目在控制成本期间需要确保施工成本和运营成本的最低值。

同时，借鉴文献［7］提出的精英策略，让适应度最大的个体直接进入下一代，以防止损失最优个体。

2.3 交叉策略

交叉策略保证种群性态的多样性。遗传算法实现交叉的方法主要有四种：一点交叉法，k点交叉法，k点杂乱交叉法，均匀交叉等［6］。本文权衡操作复杂程度与交叉效果，采用两点交叉法。

2.4 线性自适应突变策略

传统的突变策略是固定突变概率pm，这种方法简单易于实现，但不能反映种群中个体的变化趋势。还有随时间改变突变概率的策略，在遗传算法前期突变概率较大，在后期突变概率较小。此外还有利用适应度生成的早熟指标，用早熟指标作为指数函数的幂，自适应调整变异概率。

线性自适应突变策略则是根据每个个体适应度的大小确定每个个体的突变概率pm，适应度较大的个体突变概率较小，适应度较小的个体突变概率较大，适应度最大的个体不发生突变，适应度最大的个体突变概率最小。将个体适应度按从小到大的顺序排序，各个个体的突变概率为

这种策略考虑了个体自身的适应度，具有一定的灵活性，且实现比较简单。

3 考虑无功补偿的影响

配电网的无功补偿对负荷建模的影响不可忽略。无功补偿本质上具有阻抗特性，因此本文选择辨识静态负荷模型的恒电流和恒功率比例系数，其取值范围均为［0，1］，故恒阻抗的取值范围为［－2，1］，从一定程度上考虑了无功补偿的影响。

4 用改进的遗传算法辨识负荷模型参数

综合负荷模型的输入量为电压U，输出量为Y＝［P Q］T，待辨识参数为

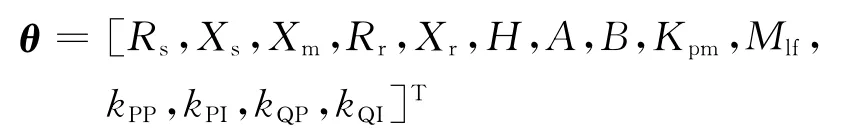
目标函数定义如下［12］：

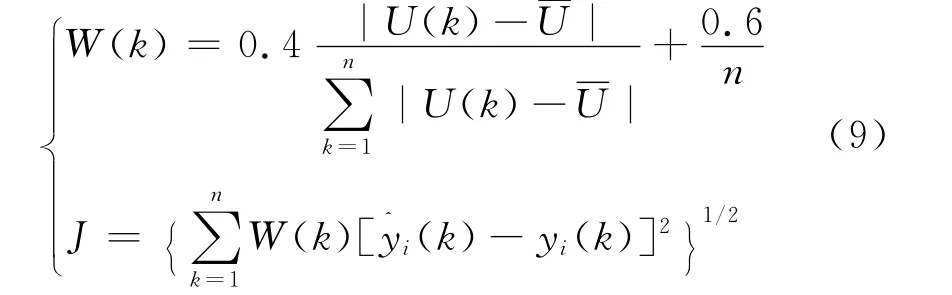
适应度函数为

使用改进遗传算法辨识综合负荷模型参数的步骤：

（1）在给定的θ取值范围内，随机生成100个初始个体。

（2）求出目标函数J及各个个体的适应度函数f。如果最优个体的适应度满足误差要求或迭代次数大于最大迭代次数，迭代结束。

（3）根据比例选择策略和各个个体的适应度，选择优良个体进入下一代，最优个体不参与选择，直接进入下一代。

（4）根据两点交叉策略，对经过选择的个体进行交叉操作。

（5）根据线性自适应变异策略进行变异操作。至此，由父代个体得到子代个体，转入（2）继续。

5 实例验证

采用本文的改进遗传算法，使用MATLAB编程，对山东电网负荷节点的实测数据进行负荷模型参数辨识，在相同的精度条件下，与基本遗传算法的辨识结果进行了比较。仿真结果见图1和图2，辨识的模型参数见表1，限于篇幅，只列出一组数据的辨识结果。图2和图3是某实测负荷响应和辨识得到的负荷模型的响应，其中实线为实测数据，虚线为模型响应数据。

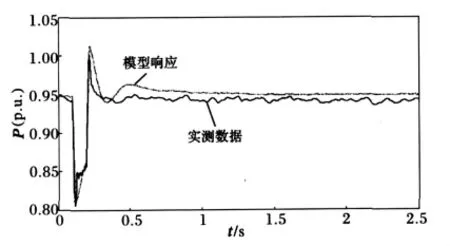
图2 有功拟合曲线Fig.2 Fitted curve of active power

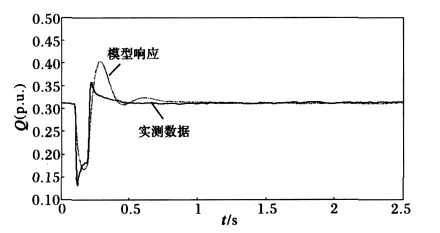
图3 无功拟合曲线Fig.3 Fitted curve of reactive power

表1 三种GA辨识的模型参数的比较Tab.1 Parameter comparison of three GA identification models

可见，在给定的允许误差范围，改进的遗传算法辨识负荷模型参数所需的迭代次数最少，固定选择概率和变异概率的基本遗传算法所需的迭代次数最多。同时在每次迭代中，改进遗传算法由于改进选择和变异策略的增加的计算是微不足道的，因此改进遗传算法是一种优秀的辨识算法。

大量仿真结果表明，采用本文的改进遗传算法，一般迭代1～5次可达到需要的精度；只改进选择策略，一般迭代4～8次可达到需要的精度；基本遗传算法一般需要迭代10次以上。辨识得到的结果也比较稳定，能从一定程序克服模型参数的分散性问题。

6 结论

本文在基本遗传算法的基础上，设计了比例选择策略和线性自适应变异策略，并将其成功应用于基于现场实测数据的综合负荷建模。同时通过调整辨识模型参数与取值范围，从一定程度上考虑了无功补偿的影响。建模实践表明，在给定的允许误差范围内，这种改进的遗传算法的收敛速度比基本遗传算法有明显的改进，实现也比较简单，能从一定程度克服模型参数的分散性，因此是一种实用的负荷建模方法。

［1］ 鞠平（Ju Ping）.电力系统负荷建模理论与实践（Theory and practice of load modeling in power systems）［J］.电力系统自动化（Automation of Electric Power Systems），1999，23（19）：1－7.

［2］ Price W W，Casper S G，Nwankpa C O，et al.Bibliography on load models for power flow and dynamic performance simulation［J］.IEEE Trans on Power Systems，1995，10（1）：523－538.

［3］ 石景海，贺仁睦（Shi Jinghai，He Renmu）.动态负荷模型多曲线拟合参数辨识（Parameter identification of dynamic load model using multi－curve fitting method）［J］.电力系统自动化（Automation of Electric Power Systems），2003，27（24）：18－22.

［4］ 韩祯祥，文福拴（Han Zhenxiang，Wen Fushuan）.模拟进化优化方法简介（An introduction to the optimization methods by simulated evolution）［J］.电力系统自动化（Automation of Electric Power Systems），1995，19（12）：5－10.

［5］ Goldberg D E.Genetic Algorithms in Search，Optimization and Machine Learning［M］.USA：Addison Wesley Publishing Company，1989.

［6］ 云庆夏.进化算法［M］.北京：冶金工业出版社，2000.

［7］ 金群，李欣然，刘艳阳，等（Jin Qun，Li Xinran，Liu Yanyang，et al）.一种改进遗传算法及其在负荷建模中的应用（An improved genetic algorithm and its application to load modeling）［J］.电力系统及其自动化学报（Proceedings of the CSU－EPSA），2006，18（2）：35－40.

［8］ 李欣然，李培强，金群，等（Li Xinran，Li Peiqiang，Jin Qun，et al）.负荷建模参数辨识中综合改进遗传算法的应用（A synthetically improved genetic algorithm in power load modeling）［J］.湖南大学学报：自然科学版（Journal of Hunan university：Natural Sciences），2007，34（2）：46－50.

［9］ 李欣然，金群，刘艳阳，等（Li Xinran，Jin Qun，Liu Yanyang，et al）.遗传策略的综合改进及其在负荷建模中的应用（Synthetic improvements of genetic strategies and their application in power load modeling）［J］.电网技术（Power System Technology），2006，30（11）：40－46.

［10］陈国良，王煦法，庄镇泉，等.遗传算法及其应用［M］.北京：人民邮电出版社，1996.

［11］朱守真，沈善德，郑宇辉，等（Zhu Shouzhen，Shen Shande，Zheng Yuhui，et al）.负荷建模和参数辨识的遗传进化算法（Evolutionary programming algorithm for load modeling and parameter identification）［J］.清华大学学报：自然科学版（Journal of Tsinghua University：Science and Technology），1999，39（3）：37－40.

［12］石景海（Shi Jinghai）.考虑负荷时变性的大区电网负荷建模研究（Load Modeling of Large－scale Power Grid Considering Time－variant Characteristic）［D］.北京：华北电力大学电气与电子工程学院（Beijing：School of Electrical and Electronic Engineering，North China Electric Power University），2004.

［13］翁俐民，王渺（Weng Limin，Wang Miao）.改进的遗传算法在谐波抑制中的应用（Application of improved genetic algorithm to restrain harmonics in distribution system）［J］.电网技术（Power System Technology），2000，24（4）：23－26.

［14］韩民晓（Han Min－xiao）.人工神经网络及其在负荷建模中的应用（ANN and Its Application to Load Modeling）［D］.北京：华北电力大学电气与电子工程学院（Beijing：School of Electrical and Electronic Engineering，North China Electric Power University），1995.

［15］周远晖，陆玉昌，石纯一（Zhou Yuanhui，Lu Yuchang，Shi Chunyi）.基于克服过早收敛的自适应并行遗传算法（Adaptive and parallel genetic algorithm based on solving premature convergence）［J］.清华大学学报：自然科学版（Journal of Tsinghua University：Science and Technology），1998，38（3）：93－95.