滑动窗Walsh基函数神经网络检测电能质量扰动①

姜孝华，彭啸亚，肖秀春，2

（1.中山大学信息科学与技术学院，广州 510275；2.广东海洋大学信息学院，湛江 524025）

近年来，随着电网中非线性负载的大量增加和敏感电子设备的推广应用，电能质量问题日益严重。为了改善电能质量，要求供电部门首先对暂态干扰源进行检测、识别和分类，进而采取合理措施改善电能质量［1］。常见的动态电能质量扰动包括：电压凸起、电压凹陷、电压间断、谐波，振荡和暂态脉冲等。电能质量扰动的检测最新的研究方法主要有时频分析方法［2，3］，能量特征估计方法［4］，小波和神经网络方法［1，5～8］等，本文基于信号的自适应分解原理，从函数分解角度，结合信号处理的特点与要求，提出了一种自适应确定隐层神经元个数及权值计算的自适应基函数神经网络模型。利用Walsh基函数神经网络对信号进行分解，根据最大能量投影原则自适应调整得到最优化的激励函数和网络权值。在此神经网络的基础上加入滑动窗利用各时刻各Walsh基上能量的变化特征实时检测出电能质量扰动类型。

1 基函数神经网络参数自适应确定方法以及收敛性分析

考虑图1所示的神经网络模型［9］，设一内积空间中的函数f（x）可用一组特定基函数｛φi（x）的线性组合来表示，考虑从｛φi（x）｝i∞＝1中择优选取基函数组来逼近f（x），则有其中e（x）为逼近误差函数。定义‖e（x）‖2为神经网络的误差逼近指标。

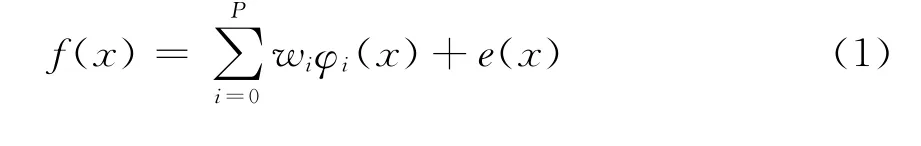
图1 基函数神经网络模型结构Fig.1 Basis－function feedforward neural network model

该神经网络的参数自适应求解过程如下：

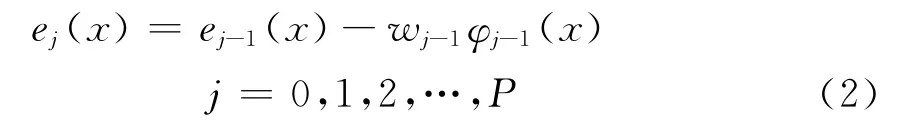
j＝0时ej（x）＝f（x），j≥1时ej（x）是ej－1投影于基函数φj－1（x）的投影与ej－1（x）的差值，其中

即ej（x）与φj（x）作内积。φj（x）的选择原则是先计算（x）在基函数系｛φi（x）中φi（x）的投影

取wi最大时对应的φi（x）作为第j个基函数。设φj（x）是归一化的函数，‖φj（x）‖＝1，则：

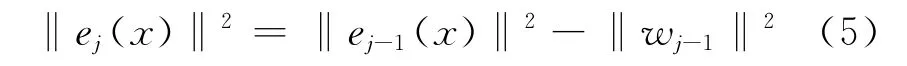
f（x）经多级分解后得误差函数

误差能量为

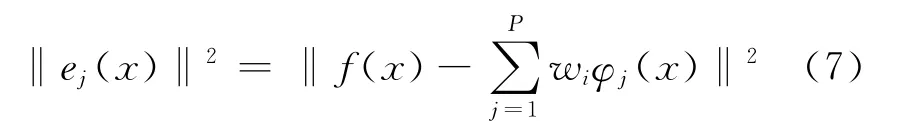
当求解至使‖ep（x）‖2小于等于某一期望的误差限时，可确定此时的神经网络结构，包括隐层神经元个数和权值。该算法集神经网络权值学习和隐层神经元个数及隐层激励函数确定为一体，简单易实现。关于该算法的收敛性，可以得出如下结论：

式（1）～（7）确定的自适应算法，当φp（x）不与ep（x）正交时，自适应过程是收敛的，即

证：令ej（x）与φj（x）之间的夹角为θj，有

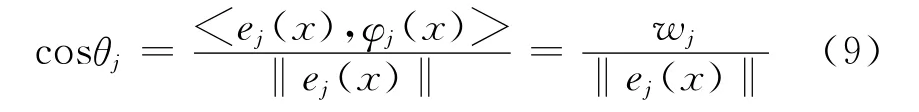
将其代入式（5）得到

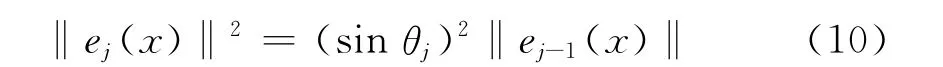
显然‖ej（x）‖2可进一步用‖ej－2（x）‖2表示，即

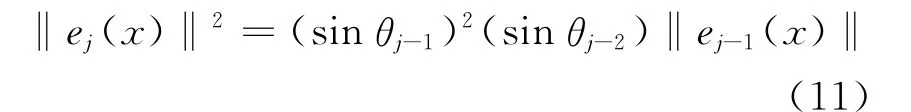
因此，经过P级分解之后，有

式中对任意的j，sin（θmax）2≥sin（θj）2，因为φj（x）不与ej（x）正交，sin（θj）2是严格小于1的，故‖f（x）‖2（sinθmax）2P单调减小趋近于0。 证毕。

2 加滑动窗的Walsh自适应神经网络

Walsh函数系是美国数学家Walsh于1923年提出的。近年来，在通信技术和信号处理等方面获得了愈来愈广泛的应用。设n的二进制表示式为n＝（npnp－1…n1）2，则列率为n的Walsh函数可表示为式（13），Walsh函数系是［0，1］区间上的完备正交系。

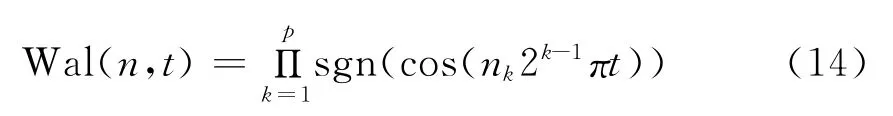
按照图1所示的基函数神经网络模型结构，以Wal（n，t）作为神经网络的激励函数建立神经网络。当网络学习完后，可以得到某一时刻的基函数的个数以及分解在各基上的权值能量。可把该神经网络看作信号在Walsh基上的分解过程，该分解过程有自适应性，寻优最佳的基和权值。该神经网络的权值包含了信号的特征信息，可以用于信号检测，为了使检测具有实时性，考虑增加时间滑动窗。由具有时频分析能力的短时傅里叶变换的思想可知，选择一个时频局部化的窗函数，假定分析窗函数g（t）在一个短时间间隔内是平稳（伪平稳）的，移动窗函数，使f（t）g（t）在不同的有限时间宽度内是平稳信号，从而计算出各个不同时刻的功率谱。而神经网络实质就是寻找信号f（t）在Wal（n，t）上的最优分解。根据短时傅里叶变换方法的思想，把该神经网络看作一个变换过程（这个过程由神经网络自身的自适应性寻优完成），在此基础上加入一个滑动窗，选滑动窗是长度为N的矩型窗（N固定不变），以便实现简单。利用该滑动窗在时域的移动可以发现在不同时刻分布在walsh基上的能量特征。这样就可以根据不同时刻的能量谱分布特征实时进行跟踪检测各种扰动信号。

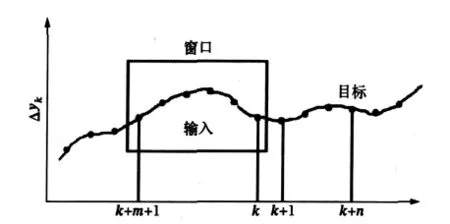
图2 短时傅里叶变换的加窗示意图Fig.2 Window diagram of short－time Fourier transform

3 实验仿真分析

3.1 在无噪声情况下的逼近能力

按照扰动信号模型，采样200个点，采样频率为10 k Hz。设置的误差精度门限值都是10－6，扰动发生在0.006 s～0.008 s。由图3可知，对包括脉冲暂态和电压间断信号在内的各种扰动信号逼近度良好。表1说明各神经网络优化的隐层个数和具体的基函数，其中用于逼近暂态脉冲的ANN基的个数较多。若要求精度降低，基函数个数可更少。

表1 无噪声时六种电能质量扰动基的数目Tab.1 Number of basis－function for six modes of power qualities without noise

3.2 加入高斯白噪声情况下的滤波效果

实验参数与图3同，加入随机高斯白噪声后，由图4实验显示该神经网络对于信号的滤波效果良好。由表2知与无噪声条件下基的个数变化不大。

表2 带高斯噪声的六种电能质量扰动基的数目Tab.2 Number of basis－function for six modes of power qualities with noise

3.3 加滑动窗后电能质量分析能量谱分布

由于各信号分解在第一、二个基上的能量是很大的，以至于分解在后面基上的能量相比起前面几个基几乎可以忽略，采样频率为20 k Hz，滑动窗tp取样点数为100。图5是当滑动窗tp在0～0.02 s滑动时，各时刻分布在各基频带上的瞬时能量谱。其中各电能质量扰动的特征分析均是对照正常电力系统的正弦信号的特征对比得出。

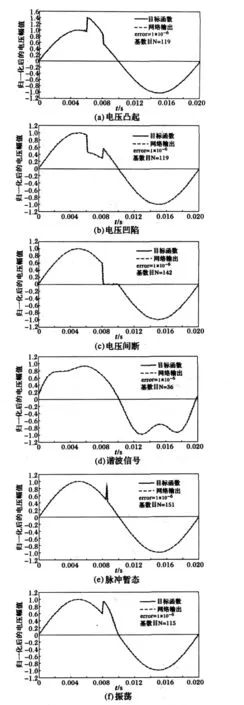
图3 无噪声情况下六种电能质量模型的逼近仿真Fig.3 Approximation results of Walsh basis－function feedforward neural network for six modes of power qualities without noise

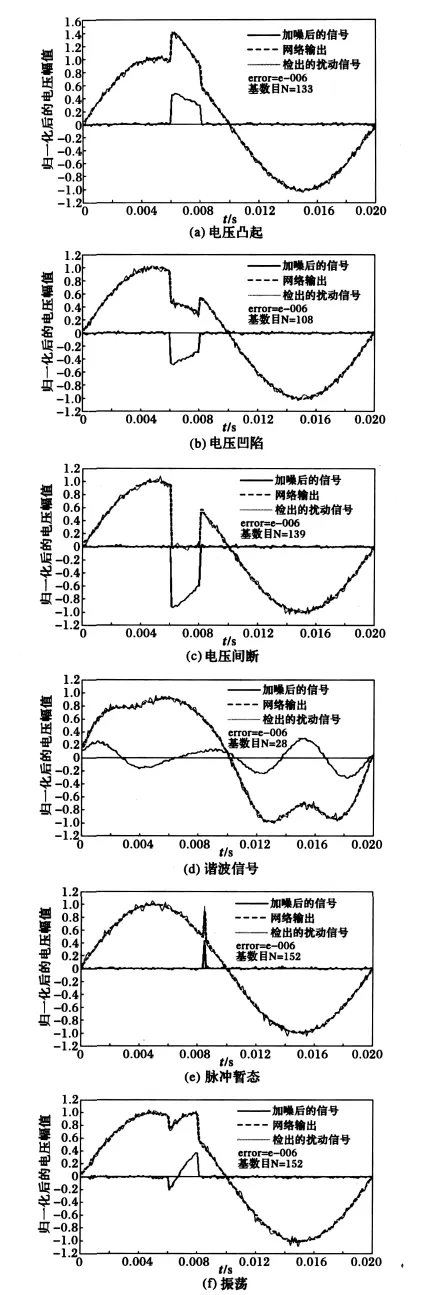
图4 带噪声情况下六种电能质量的逼近仿真结果Fig.4 Approximation results of Walsh basis－function feedforward neural network for six modes of power qualities with noise

图5 0～0.02 s六种电能质量的能量谱图Fig.5 Energy spectrum of six modes of power qualities between 0 and 0.02 s

以上电能质量扰动的能量谱图显示各种电能质量扰动均有不同的特征，能够很好地分辨出具体是哪一种扰动，且能实时跟踪检测出扰动发生的具体时间段。

4 结论

根据以上的理论分析和实验结果，表明该方法具有很好的实时检测效果，且Walsh基的特殊性在于易于用电路实现，易于用DSP芯片实现，是电力系统电能质量检测的一种有效方法。

［1］ Gaouda A M，Salama M M A，Sultan M R，et al.Power quality detection and classification using wavelet－multiresolution signal decomposition［J］.IEEE Trans on Power Delivery，1999，14（4）：1469－1476.

［2］ Wang Min，Mamishev Alexander V.Classification of power quality events using optimal time－frequency representations－Part1：Theory［J］.IEEE Trans on Power Delivery，2004，19（3）：1488－1495.

［3］ 赵凤展，杨仁刚（Zhao Fengzhan，Yang Rengang）.时频分析方法在电能质量扰动检测与识别中的应用（Application of time－frequency transform to detection and recognition of power quality disturbances）［J］.华北电力大学学报（Journal of North China Power University），2006，33（5）：33－37.

［4］ 孔英会，车辚辚，孙中伟，等（Kong Yinghui，Che Linlin，Sun Zhongwei，et al）.基于能量特征估计的电能质量扰动消噪方法研究（De－noising method of power quality disturbance based on energy features estimation）［J］.华北电力大学学报（Journal of North China Power University），2008，35（4）：87－92.

［5］ Xuhua Yang，Huaping Dai，Youxian Sun.SIMO Fourier neural networks research［C］∥IEEE Intelligent Transportation Systems Conference，Shanghai，China：2003.

［6］ Poisson Olivier，Rioual Pascal，Meunier Michel.Detection and measurement of power quality disturbances using wavelet transform［J］.IEEE Trans on Power Delivery，2000，15（3）：1039－1044.

［7］ Santoso Surya，Powers Edward J，Grady W Mack，et al，Power quality disturbance waveform recognition using wavelet－based neural classifier－Part 2：application［J］.IEEE Trans on Power Delivery，2000，15（1）：229－235.

［8］ 王继东（Wang Jidong）.基于二进小波变换的电能质量扰动检测（Detection of power quality disturbance based on binary wavelet transform）［J］.电力系统及其自动化学报（Proceedings of the CSU－EPSA），2007，19（1）：100－103.

［9］ 梁久祯，何新贵（Liang Jiuzhen，He Xingui）.有理式多层前馈神经网络（Rational fraction multiplayer feed forward neural networks）［J］.控制与决策（Control and Decision），2004，19（3）：349－350，354.