火灾下钢筋混凝土构件的弹塑性本构模型
2011-04-12王振清白丽丽
苏 娟 王振清 徐 辉 白丽丽
(哈尔滨工程大学建筑工程学院1) 哈尔滨 150001)
(海洋石油工程股份有限公司2) 天津 300451) (烟台南山学院3) 烟台 265713)
0 引 言
建筑结构在正常服役期内遭受实际火灾时,温度的升高使截面产生不均匀的温度场,进而导致材料性能的严重劣化以及应力、内力的剧烈重分布,因而其结构反应分析可以归结为非线性弹塑性问题.国内外几乎都采用由经典的流动法则理论建立的应力-应变本构模型对该问题进行分析[1-3].但是在实际结构中,由温度引起的热应力、塑性流动以及随等效应变和温度变化的屈服准则耦合在一起,采用经典的本构模型的分析结果与构件在实际火灾中的表现有一定差距.因此,本文结合文献[4]提出的弹塑性模型,应用 流动理论,在屈服函数中考虑了塑性等效应变与温度的耦合作用,从而导出了高温下钢筋混凝土构件材料弹塑性增量本构模型.在此基础上,基于非线性连续介质力学原理,采用有限元对该本构模型进行了分析计算,数值结果与现有的试验模型基本吻合,为钢筋混凝土结构在高温下耐火性能分析提供了依据.
1 本构模型
由于温度的影响,结构材料的弹性模量、泊松比、屈服极限、极限强度等都是温度T的函数.设给定温度场 T(xi,yi,t).xi,yi为位置坐标;t为时间.采用弹塑性模型,则总应变为

式中:ε,εe,εp,εT分别为结构的总应变张量、弹性应变张量、塑性应变张量和温度应变张量.应力张量σ与弹性应变张量εe之间满足Hooke定律
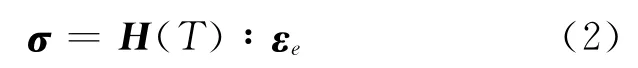
式中:H(T)为四阶弹性刚度张量,表达式如下

其中:G(T)为剪切模量;K(T)为体积模量;δ为二阶Kronecker delta单位张量为特殊等同张量,定义为

式(2)对“类时间参数”求导有增量表达式
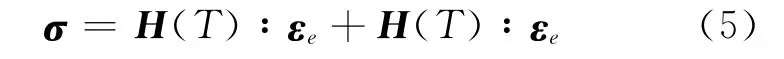
温度变形张量为

式中:α(T)为热膨胀系数;T,T0为瞬时温度与初始温度;I为二阶单位张量.温度变形张量的增量形式
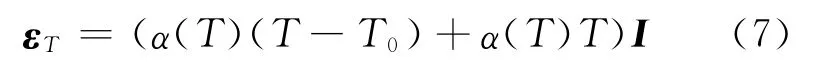
在考虑温度影响的情况时,由于材料的屈服强度一般是温度的函数,因此弹塑性材料的屈服准则中的屈服函数应当看作温度T、各向同性硬化系数β和屈服强度张量σY的函数.本文假设材料塑性服从混合硬化状态(如图1所示)的情形,由文献[5]可知考虑温度影响和不考虑温度影响的后继屈服面在形式上是相似的,则由J2流动理论可知材料的屈服条件的为

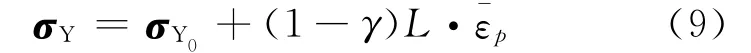
式中:σY0,为初始屈服强度和等效塑性应变;γ∈[0,1]为权重因数;L为四阶硬化系数张量,见图2.

图1 两种强化模型示意图

图2 单向拉伸情况的弹塑性硬化增量

各向同性硬化系数增量dβ为
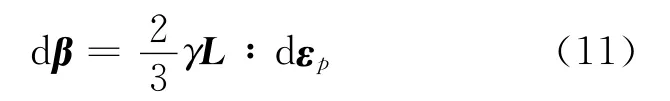
由式(8)可知“一致性条件”如下

塑性应变张量变形率dεP可由V.Mises流动法则得出


将式(13)~(17)代入式(12)可得正交流动因子dλ
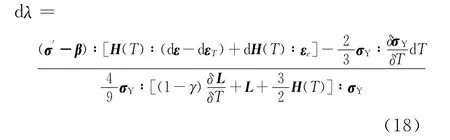
将式(17)、(18)代入式(5)可得火灾作用下钢筋混凝土结构材料的弹塑性本构方程为

其中四阶弹塑性矩阵Hep和初始应力dσ0为

2 本构模型的求解方法
以dε和dT为主要变量进行迭代,由每一增量步或每次迭代求得应力增量dσ,决定新的弹塑性状态的基本步骤.
步骤1 利用几何关系计算应变增量(或其修正量)

步骤2 按弹性关系计算应力增量的预测值以及应力的预测值

步骤3 按单元内各个积分点计算H(T)的预测值.
假设在升温过程中应力、应变按比例变化,计算屈服函数值f(T+ΔTσ,Tβ,TσY),分3种情况计算比例因子m[6].
步骤3.1 若f(T+ΔTσ,Tβ,TσY)≤0,则该积分点为弹性加载,或由塑性按弹性卸载,比例因子m=1;
步骤3.2 若 f(T+ΔTσ,Tβ,TσY)>0 且f(Tσ,Tβ,TσY)<0,则该积分点为由弹性进入塑性的过渡情况,应由f(Tσ+mΔσ,Tβ,TσY)=0计算比例因子m.此时对应的温度为应力达到屈服面的屈服温度;
步骤3.3 若 f(T+ΔTσ,Tβ,TσY)>0 且f(Tσ,Tβ,TσY)=0,则该积分点为塑性继续加载,这时m=0.
步骤4 对于步骤3.2、步骤3.3两种情况,均有对应于弹塑性部分的应变增量
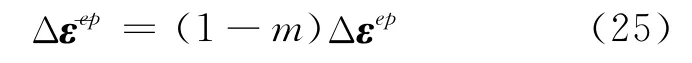
通过对弹塑性本构方程进行积分,最终可以得到本步应力增量Δσ
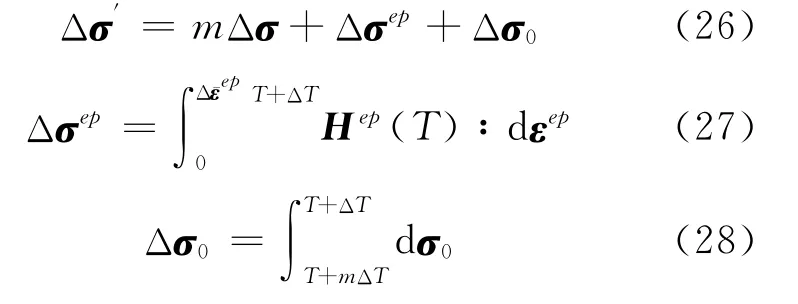
则按弹性关系计算应力增量的预测值以及应力的预测值

式中:T+ΔTσ,T+ΔTH(T)分别为 T+ΔT 温度下的应力与弹性刚度张量;Tσ,Tβ,TσY分别为T 温度下的应力、各向同性硬化系数和屈服强度张量.
3 试验验证
3.1 材料的力学性能
由于温度的影响,结构材料的弹性模量、泊松比、热膨胀系数、屈服极限、极限强度等都是温度T的函数,本文选用文献[7]中相关的材料高温力学性能.
3.2 算例
根据本文所提的基于塑性力学用张量表示的钢筋混凝土结构材料的弹塑性本构模型,采用了一类无条件稳定、收敛速度有保证的非线性有限元来实现算法,编制了相应的程序.以C30混凝土立方体和HRB335钢筋为例对该模型进行了数值模拟[8],并与其他学者所提及的基于试验的本构模型进行了比较(如图3、图4).比较发现本模型的结果与各经验公式趋势一致,验证了模型的正确性和有效性.
4 结 论
实际结构中,由温度引起的热应力、塑性流动以及随等效应变和温度变化的屈服准则耦合在一起,采用经典本构模型的分析结果与构件在实际火灾中的表现有一定差距.本文应用J2流动理论用张量表示法导出了高温下钢筋混凝土构件弹塑性增量本构模型,编制了求解该模型的有限元求解程序.从而避开了经典本构关系带来的困难与缺陷,进一步验证了试验本构模型的正确性,为钢筋混凝土结构在高温下耐火性能分析提供了依据.

图3 高温时C30混凝土的受压应力-应变全曲线

图4 高温时HRB335钢筋的受压应力-应变全曲线
[1]Nechnech W,Meftah F,Reynouard J M.An elastoplastic damage model for plain concrete at high temperatures[J].Engineering Structures,2002,24(5):597-611.
[2]茅云生,侯 磊,王呈方.板材弯曲伸长的理论研究[J].武汉理工大学学报:交通科学与工程版,2002,26(5):592-595.
[3]高立堂,宋玉普,董毓利.火灾下钢筋混凝土板的热弹塑性有限元分析——基于S-R分解原理(I:理论)[J].计算力学学报,2007,24(1):86-90.
[4]黄克智,黄永刚.固体本构关系[M].北京:清华大学出版社,1999.
[5]Seong Hoon Kang,Yong Taek Im.Three-dimensional thermo-elastic-plastic finite element modeling of quenching process of plain-carbon steel in couple with phase transformation[J].International Journal of Mechanical Sciences,2007,49(4):423-439.
[6]高立堂.无粘结预应力砼板火灾行为的试验研究及热弹塑性有限元分析[D].西安:西安建筑科技大学土木工程学院,2003.
[7]过镇海,时旭东.钢筋混凝土高温性能及其计算[M].北京:清华大学出版社,2003.
[8]钮 宏,陆州导,陈 磊.高温下钢筋与混凝土本构关系的试验研究[J].同济大学学报,1990,18(3):287-297.
