三视图能否正确而完整表达简单形体的探讨

2011-04-10西南石油大学机电工程学院四川成都610500

长江大学学报(自科版) 2011年34期

(西南石油大学机电工程学院，四川成都610500）

对于学习机械制图者来说，三视图是需要掌握的一种最基本的视图表达方法[1-2]，因为其可反映实形、作图简便、利于图示和图解，并且在一个形体按正确的方位摆放好后，其基本的三视图是唯一确定的，不象向视图、剖视图等可能会有多种表达方式。此外，在生产实践中，三视图是应用最为广泛的一种视图方法。正是由于三视图使用的广泛性，在人们的直观印象里，觉得单从完整性上考虑，任何一个形体好象都可以用三视图来完全表达。笔者查阅了相关资料，发现大多数书籍文献并没有对三视图的唯一确定性进行具体说明，基本上都是一笔带过，如 “有些机件的外形和内形都较复杂，仅用三视图和‘可见部分画粗实线，不可见部分画细虚线’的方法不可能完整、清晰地把它们表达出来[3]。”这种简单的描述显然不能说明三视图就不能唯一表达一个形体。换句话说，给出一组三视图，根据视图构想出的形体是否唯一，还没有得到理论性的证明。要想证明上述问题，最简便的方法是找出一个反例。下面，笔者对三视图能否正确而完整表达简单形体进行讨论。

1 问题的提出与讨论

1．1 关于该问题的相关说明

如果在一组三视图中，如果能找出2种或2种以上的形体完全符合这组三视图，那就可以证明三视图不能完整而唯一表达一个形体。笔者认为，这种找寻只能从简单形体入手。因为较为复杂的零件图或装配图也许用三视图不能完全表达，但这种说明极其繁杂，将零件图或装配图改成三视图更是难上加难。所以，研究重心应该是简单形体。对于点、线、面这些最基本的元素甚至更多简单形体，仅用2个视图就可以完全表达。根据2个视图，可以找出另外1个视图。上述过程涉及到许多几何方法，如 “长对正，高平齐，宽相等”或者其他特殊的方法(换面法）等[1-2]。即使是很复杂的曲线投影如相贯线的投影，利用三视图来表达也是唯一的，只是其度量稍显复杂[4]。所以，利用三视图来表达已经相当完备。笔者尝试从视图的 “盲区”来找切入点，即让左视图的外轮廓线把 “后面”的线遮掩住，使得视图所表达出的形体有多解。笔者终于在解题过程中发现了一个反例。下面，对该例题进行简要分析。

1．2 例题分析

图1所示为例题图。从图1可以看出，最左边的上下2个视图分别是三视图中的主视图和俯视图。该题的主视图和俯视图完全相同，都是正方形里面加两条竖线。右边4个选项分别是这个形体可能出现的4种左视图。该例题的要求是根据4种左视图找出三视图所表达的4个形体。

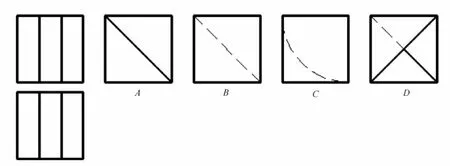
图1 例题图

很明显，该例题想说明仅用2个视图有时并不能完全表达一个形体，比如该题中仅给出主视图和俯视图，左视图就可能会出现多种情况。

对于图1中A、B、C选项所表达的形体，直接给出其实体图，如图2所示。

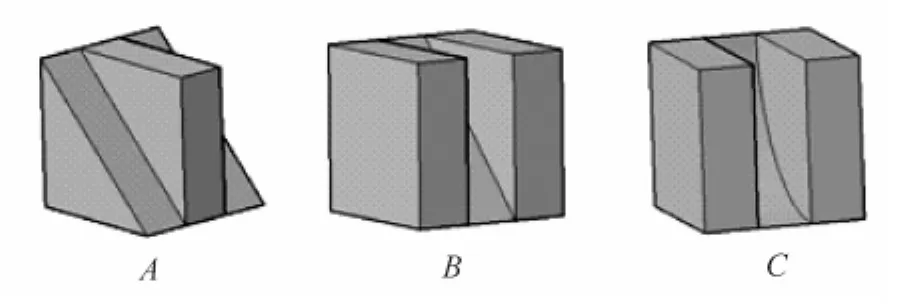
图2 ABC选项的立体图

需要说明的是，对于C选项，其实还可以延伸出其他几种情况。该选项的圆弧是右上凹的，其实还可以右上凸。同时，虚线也可以转为实线。这几种情况均满足主视图和俯视图，都能表达出不同的形体。

对图1中的D选项进行重点分析，因为通过D选项可以找出反例。首先，从左视图上来看，其复杂程度要略高于其他3个选项，可以采用分割的办法进行分析。该形体从主视图和俯视图上来看，可以分为3个部分。按由近及远的顺序可以看出，第1部分为1个直角三棱柱，第2部分也是1个直角三棱柱，只是摆放方式不同，导致第2部分的上半部分会被第1部分遮挡，从而出现虚线。对于第3部分，直角三棱柱和长方体都满足要求而形成独立的形体(见图3），因而三视图的确不能完整唯一表达一个形体。

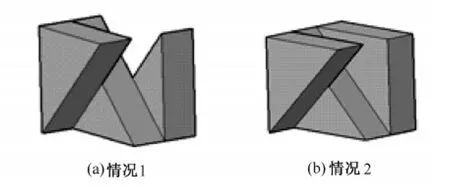
图3 D选项的2种实体图

绝大多数形体都可以用三视图完全表达，为何出现上述情况呢？要解释该问题，可以对D选项左视图中的顶点和交点加以编号，如图4所示。

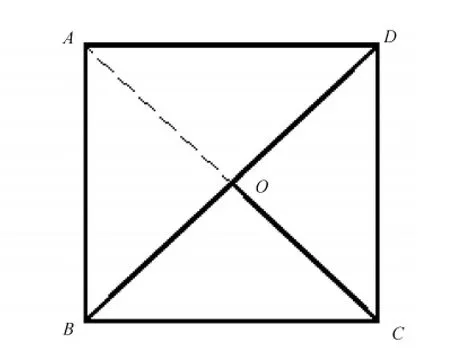
图4 D选项分析图

图4是一个从左向右看的视图，研究者仅仅只是将从该角度看到的图形绘制成图，后面看不见而未被粗实线遮挡的地方用虚线表示。所以，在投射过程中，如果后面的线条被前面的粗实线所遮挡——也就是后遇到投射线，则该线条为不可见，在图中不能表现出来。比如第3部分的图形为三棱柱时(见图3（a）），投影出来应该是一个三角形，而图4中的CD边即为该三角形的可见部分，另外2条边被CB边和BD边所遮挡，为不可见。所以在该情况下，第3部分的加入，仅仅追加了一条粗实线(线段CD）而已。

如果第3部分是长方体，投影出来的应该是正方形。图4中CD边即为正方形的可见部分，而正方形的另外3条边全被遮挡。从结果上看，第3部分的加入仍然只是多出了一条粗实线而已，因而上述2种情况同时满足主视图和俯视图的要求。

通过以上分析发现，导致该三视图有多解的症结在于视图的可见与不可见。有关视图的可见与不可见的问题涉及到机械制图中的一个相当重要的概念，即重影点，与此相关的概念是重影线。

2 重影点及重影线的分析

重影点的基本定义是当空间2点位于垂直于某投影面的同一条投射线上时，2点在该投影面上的投影重合，则该2点叫做重影点。在投射过程中，重影的2点中先遇到投射线者为可见，后遇到投射线者被前者遮挡，为不可见。

应用重影点可以判断2条直线的相对位置，是相交还是交叉[5]，分别如图5和图6所示。

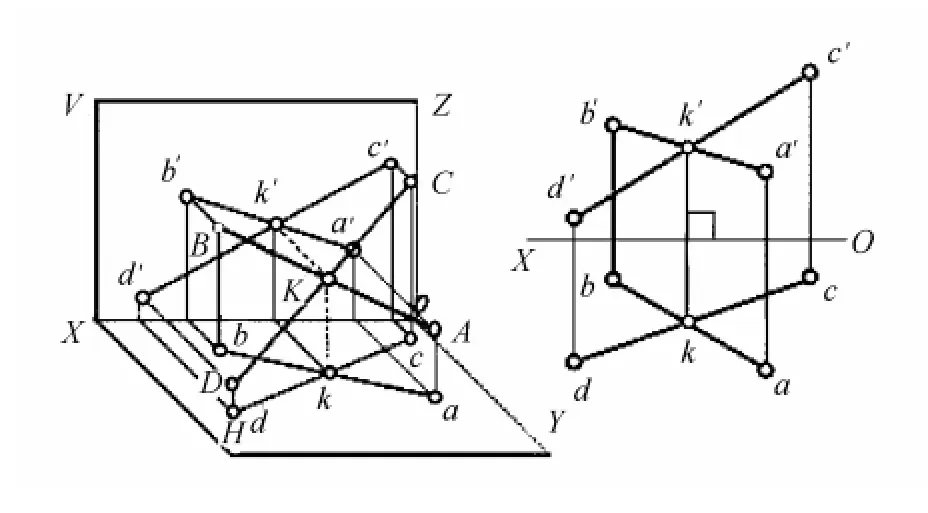
图5 2直线相交图

图6 2直线交叉图

由图5可知，如果AB、CD2条直线相交，那么H面和V面中的2个交点k和k′的连线应该垂直于投影轴OX轴。由图6可知，如果AB、CD2条直线交叉，则1′、3点连线不垂直于OX轴，视图中的2个交点均为重影点。通过重影点，可以很清晰地判断2条直线在另一个投影面上的前后关系。

重影点还可以应用于直线与平面的位置关系以及平面与平面的位置关系中。

当点排列成为线时，根据重影点的概念，可以衍化出重影线的概念，即空间中的2条直线，只要其中有一条直线上的任意一点都能在另一条直线上找到唯一并且不同的点，这2点同时通过投射线，则2条直线被称为重影线。如上述反例就可以用重影线来进行说明。反例中提到的2种可能情况，都是因为在左视图上无法判断有无重影线。因为重影线只有先遇到投射线者可见，所以 “后方”的直线成为 “盲区”，导致最终产生了多种不同情况。因此，无法判断出重影线的有无才是导致三视图不能完全唯一表达一个形体的根本原因。