一类系数固定的解析函数族
2011-11-18李小飞
李小飞,解 进
(长江大学工程技术学院,湖北 荆州 434020)
一类系数固定的解析函数族
李小飞,解 进
(长江大学工程技术学院,湖北 荆州 434020)

单叶;解析;凸;Salagean算子
设函数f(z)在单位圆盘U={z:|z|<1}内单叶解析且有如下泰勒展开式[1]:
(1)
记其族为S,Salagean[2]定义了Salagean算子D如下:
D0f(z)=f(z)D1f(z)=Df(z)=zf′(z)Dnf(z)=D(Dn-1f(z)) (n=0,1,2,…)

记Sn(α)表示S中满足下面不等式的函数族:

并记Sn(α,β,γ)表示S中满足下面不等式的函数族:
显然Sn(α)⊂Sn(0,β,1)。文献[3]对Sn(α)做过研究;文献[4]对Sn(α,β,γ)做过研究并有下面引理。
引理1[4]形如式(1)的函数f(z)∈Sn(α,β,γ)当且仅当:


(2)
1 系数估计定理

证明取:

并利用引理1的结论即可得到上述结论。取:

结论是精确的。

2 闭凸包定理



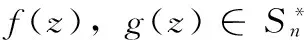

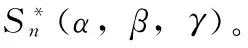

(3)
则:
(4)
证明由fj(z)和F(z)的定义,知:
则:
3 偏差定理



因为:
所以:
则:
同理:




[1]余家荣.复变函数[M].北京:高等教育出版社,2000.
[2]Salagean G S. Subclass of univalent functions [J]. Lecture Notes in Mathematic,1983,3:362-372.
[3]Ekrem Kadioglu. On subclass of univalent functions with negative coefficients[J]. Applied Mathematics and Computation,2003,146:351-358.
[4]李小飞.一类负系数单叶解析函数族[J].黄冈师范学院学报,2009(3):16-21.
[5] Darwish H E.On the coefficients of some subclass of univalent functions[J]. Southeast Asian Bulleitin of Mathematics,2001,25:75-86.
[6]Kim H S L.Some class of univalent functions[J].Math Japan,2003,5:781-796.
[编辑] 洪云飞
10.3969/j.issn.1673-1409.2011.12.003
O174.51
A
1673-1409(2011)12-0007-02
