分析水中结构自由振动的三维附加质量矩阵法

张文鹏 宗 智

大连理工大学工业装备结构分析国家重点实验室运载工程与力学学部 船舶工程学院，辽宁 大连116024

分析水中结构自由振动的三维附加质量矩阵法

张文鹏 宗 智

大连理工大学工业装备结构分析国家重点实验室运载工程与力学学部 船舶工程学院，辽宁 大连116024

船舶总体振动分析需考虑对船体外部水的影响。通过建立水域三维有限元模型进行计算或者先计算出附加质量后，加入到结构质量中进行计算。随着有限元技术的发展，船舶大都采用三维有限元建模。传统方法，例如刘易斯附加水质量法，虽然考虑到纵向变形，但确没有忽略船体横剖面的变形，因而不够准确。采用三维边界元方法，考虑水中结构振动的三维效应，计算三维附加质量矩阵，并对水中结构振动进行分析。结果表明，水中结构振动是三维变形，应该采用三维附加质量矩阵进行振动分析。

水中结构；三维附加质量矩阵；自由振动分析；湿模态

1 引言

船体是一种复杂的弹性结构，船舶在航行过程中会受到各种激振力的作用而产生不同程度的振动，例如波浪激励振动，主机、螺旋桨激励引起的振动等。因此，能够准确预报船体结构振动的固有频率及响应，从而避免共振并降低振动响应，对于船舶设计而言十分重要。相关研究也有许多，例如Lin等［1］研究了复杂船体结构振动特性和振动的控制，Franois等［2］研究了主机和螺旋桨对船体及上层建筑的影响。

船舶是在水中航行，因此在对船舶总体振动进行分析时，要考虑水对水中结构振动造成的影响。孙士丽等［3］采用湿模态方法对单面浸水的板、加筋板的振动特性进行计算。吴芳等［4］通过Ansys计算拟合了单面浸水板的附加质量系数曲线，并计算了单面浸水板的固有频率。夏利娟等［5］通过二维有限元法和二维边界元法，分别计算船体结构和流体，并计算了高速船的垂向振动。孙洋等［6］采用刘易斯方法计算了船体总体振动固有频率，对水平弯曲—耦合振动进行了修正，并给出了修正系数。文献［7］采用改进二维边界元法，计算无限流场中不规则截面物体的附加质量。

对于复杂的弹性结构的振动问题，需要采用数值计算方法进行分析。通用有效的数值方法是有限元法［8］，目前船舶大都采用三维有限元建立模型。考虑到水对船体振动造成的影响，可以采用建立结构和水域的三维有限元模型进行整体计算；或者先计算出水中结构附加质量，然后加入到结构质量中进行计算。文献［9］就是采用建立结构和水域的三维有限元模型的方法，研究了空气和水中多舱段复杂壳体的振动模态特性。

计算附加质量的方法，只需考虑固液交界面的流体，计算量小且计算效率高。但目前国内对于附加质量对水中结构振动的影响的处理，基本都是采用刘易斯附加水质量法或者二维边界元方法。这些方法将船体看作自由梁，假设每一个横剖面都在做刚体运动，然后采用刘易斯或者二维边界元方法计算出每个剖面作刚体运动的附加质量，沿船长积分得到整船的附加质量。再将整船的附加质量除以船体湿表面积，得到附加水密度，加到船体与水接触的外板的密度上，然后分析船体振动。该方法考虑了沿船长方向结构变形的影响，但是未计及沿横剖面结构变形产生的影响。

现在的有限元建模并不是简化成梁模型，而是更为复杂的三维模型。在横剖面上两个单元之间的相对变形会对流体产生影响，如果不考虑这种影响，而将横剖面视为刚体，采用刘易斯法或者二维边界元方法，从理论上讲是错误的。

本文采用三维边界元方法计算水中结构的附加质量矩阵。首先，考虑三维结构变形与流体的耦合效应及对附加质量的影响，使得进行水中结构自由振动分析更加准确。然后，对三维附加质量矩阵和理论解进行了对比验证，结果证明所计算的三维附加质量矩阵是正确的。在此基础上，采用湿模态法进行水中结构自由振动分析，计算了在水中自由振动的固有频率以及振型。

2 附加质量矩阵计算及湿模态理论

1978年，Deruntz等开始采用边界元方法计算无限流场中结构振动的附加质量［10］。本文也采用边界元方法，来计算流场中结构的附加质量矩阵。

2.1 流场中速度势及其导数

假定流体是无粘、无旋、不可压缩的理想流体，定义无限流场速度势：

速度势的定解问题为：

上面定解问题的解，可以采用简单格林函数分布源模型来表达，并假定采用常数源，即在每个划分的湿表面单元上源强是固定值：

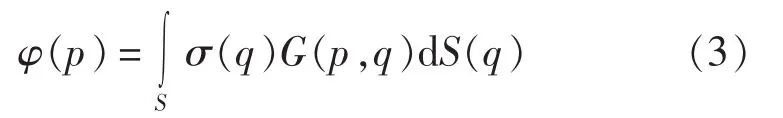
式中，q为源点；p为场点；σ（q）为源的强度；S为物体表面；G（p，q）为格林函数。

对于无限水域，格林函数为：

速度势及其导数为：

当水中结构物离水面比较近或者结构物为水面漂浮结构物时，需要考虑自由面的影响。对于较高频率的振动，自由面波动的影响可忽略不计，此时速度势的定解问题为：

在这种定解条件下，格林函数为：

这样，速度势及速度势的导数为：

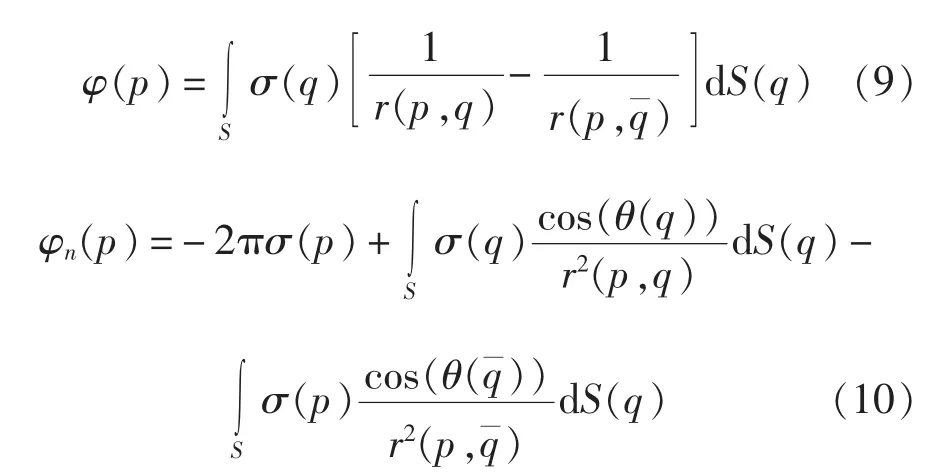
式中，q是q点关于自由水面的镜像点。

2.2 流体质量矩阵

在流域内，流体动能为：

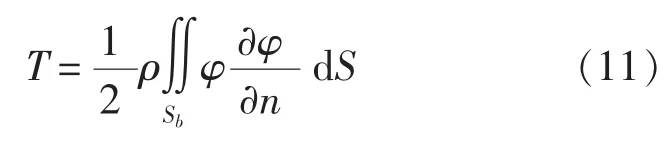
若取结构外法向（即指向流体域内）为正，则流体动能为：

在物体的表面上划分网格，则流体的动能可以表示为离散形式：

式中，φn、φ、p为相应于离散的湿表面的列向量；长度等于湿表面数量n；dS为n×n的对角矩阵。上标T表示转置。

对于常数源，速度势及其导数可以写成离散形式：

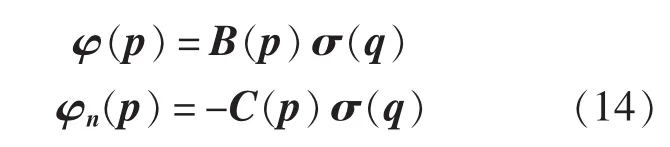
式中，σ（q）为n个元素的列向量；B（p），C（p）为n×n的满阵；p为流场内任意一点，当场点p位于湿表面单元的控制点P，即p＝P时有：

将式（14）和式（15）代入式（13），可得：

式中，

式中，C－T＝（C－1）T。由于当任意向量A非对称时，uTAu＝0，所以式（16）可以写成：

式中，

将Mf称为流体质量矩阵，或者附加质量矩阵。

2.3 水中结构湿模态

流体速度u和结构速度x˙有如下关系：

式中，D为流体单元与结构自由度的变换矩阵。将式（20）代入式（18），得

式中，Ma＝DTMfD

式（21）表明，相对应于结构的位移x、速度x˙和加速度x¨，流体的相当质量矩阵为Ma。

对于无阻尼结构振动自由振动，有如下方程

则水中无阻尼结构振动自由振动湿模态方程为：

3 附加质量矩阵计算验证

为验证附加质量矩阵计算是否正确，引入流体边界模态［11］：

式中，Af为湿表面单元面积对角阵。通过计算特征值λ，就可以验证附加质量矩阵。

以无限流场中的圆球为例，计算验证附加质量特征值。无限水域中球体振动特征值精确解为：

首先，建立无限流场中的半径为10的球体模型，并采用4个网格划分方案，计算了4种网格方案的流体边界模态特征值，并与理论解进行比较，以考察计算的误差及收敛性。圆球的模型及网格情况如图1所示，分别划分600、1 176、1 944和2 904个单元。

计算时，n取0，1，2，3，4，分别计算相应理论解和计算值，并进行比较。计算结果见表1和图2。

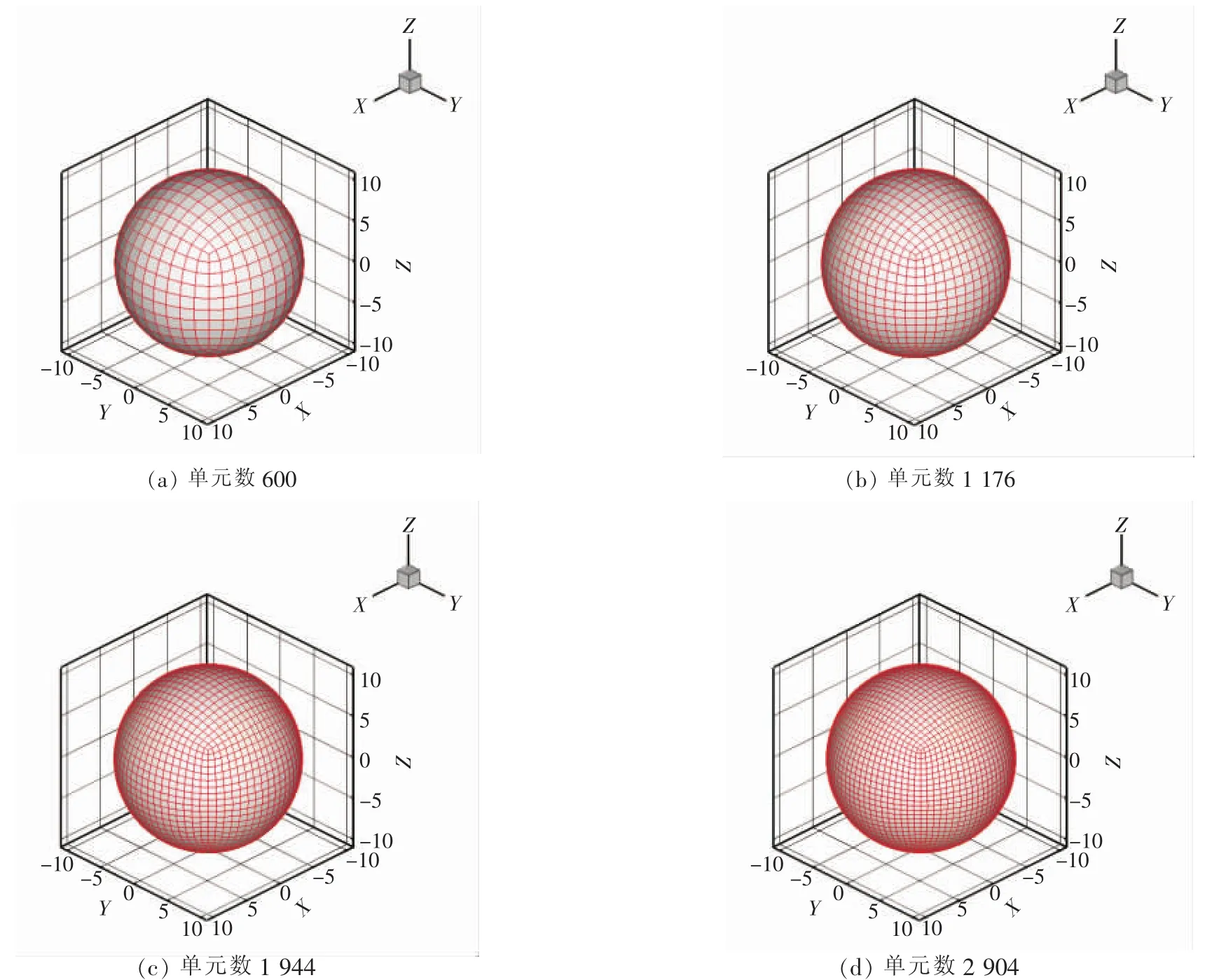
图1 圆球模型及网格Fig.1 Sphere model and its mesh

表1 无限流场中球体边界模态特征值计算及与理论解比较Tab.1 Sphere boundary modal eigenvalue calculation and comparison with theoretical solution in infinite field

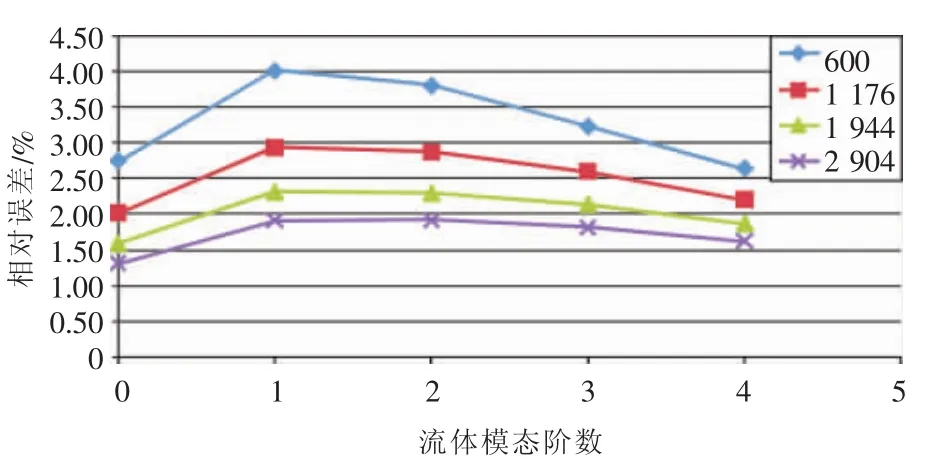
图2 特征值误差随网格数变大而减小Fig.2 Eigenvalue calculation of the convergence

从计算结果来看，对于同一个单元数，0阶模态和4阶模态的相对误差比较小，2阶或者3阶模态的相对误差最大。对于不同单元数，单元数越小，相对误差越大，相对误差最小的是2 094单元的情况，其最大相对误差为1.919%；相对误差最大的是600单元的情况，但其最大相对误差也只有4%，这个相对误差是在工程允许范围内的。随着网格单元数的变大，相对误差减小，说明计算是收敛的。

4 应用三维附加质量矩阵计算水中结构振动

在验证了三维附加质量矩阵后，根据湿模态理论就可以进行水中结构的自由振动分析，计算水中结构的固有频率。计算流程为如图3所示。

以一个盒子为例代表船舶，计算其固有频率。盒子的基本参数列于表2中，盒子建模见图4。

计算情况如下，分别计算了盒子在空气中和水中的固有频率及振型，图5给出了前7阶的振型，表3给出了前10阶的固有频率。

图3 应用附加质量矩阵计算结构水中振动流程图Fig.3 Flow chart of calculation of free vibration of structure in water with added mass matrix

从计算结果来看，结构在水中的固有频率要比在空气中低，降幅从15%～38%不等，平均降幅为24.78%。水中结构的振型与空气中的振型会产生交错，例如图5中的（d）和（e）：在空气中图5中的（e）是在第3阶出现的振型，而在水中，图5中的（d）则在第2阶就出现了。

表2 盒子的基本参数Tab.2 Main particulars of a box

图4 盒子模型Fig.4 Box model

图5 盒子在空气中及水中前7阶的振型Fig.5 1st～7thmodal natural vibrations of box in the air and water

表3 盒子在空气中及水中固有频率Tab.3 Natural frequency of box in the air and water

5 结论

本文采用边界元方法计算水中结构三维附加质量矩阵的结果可靠，通过计算无限流场中球的附加质量矩阵，其特征值与理论解的最大相对误差为4%，满足工程精度。同时，随着网格的加密，相对误差减小，计算是收敛的。

其次，结构在水中的固有频率要比在空气中低，降幅从15%～38%不等，平均降幅为24.78%。水中结构的振型与空气中的振型会产生交错，在空气中较高阶数的振型在水中会提前在较低阶数出现。

最后，从计算的水中结构振型来看，横剖面会产生变形，即结构湿表面变形呈三维。因此，进行三维水中结构振动分析时，应当采用三维附加质量矩阵。

［1］LIN T R，PAN J，O＇SHEA P J，et al.A study of vibration and vibration control of ship structures［J］.Marine Structures，2009，22（4）：730－743.

［2］FRANOIS B，LUDOVIC J，LECH M，et al.Evaluation of main engine and propeller excitations of ship hull and superstructure vibration ［J］.InternationalShipbuilding Progress，2008，55（1－2）：3－27.

［3］孙士丽，王诗平，姚熊亮，等.板和加筋板流固耦合振动特性研究［C］.黑龙江省造船工程学会2008年学术年会论文集.黑龙江，哈尔滨，2008.

［4］吴芳，赵德有.水对船舶与海洋建筑物结构振动影响的研究［J］.中国海洋平台，2007，22（3）：22－26.

［5］夏利娟，吴卫国，翁长俭，等.高速船垂向振动计算的流固耦合分析［J］.上海交通大学学报，2000，34（12）：1713－1716.

［6］孙洋，赵德有.流固耦合理论在船体总振动附加水质量研究中的应用 ［J］.中国海洋平台，2008，23（3）：22－27.

［7］李华东，朱锡，罗忠，等.附连水质量的边界元法求解［J］.海军工程大学学报，2009，21（2）：45－49.

［8］金咸定，赵德有.船体振动学［M］.上海：上海交通大学出版社，2000.

［9］陈明，钱家昌，曹为午.不同介质中多舱段复杂壳体的振动模态特性研究［J］.噪声与振动控制，2009，29（2）：1－5.

［10］DERUNTZ J A，GEERS T L.Added mass computation by the boundary integral method［J］.International Journal for Numerical Methods in Engineering，1978（12）：531－550.

［11］GEERS T，DOUBLY L.Asymptotic approximations for transient motions of submerged structures［J］.Journal of the Acoustical Society of America，1978，64 （5）：1500－1508.

3D Analysis Method for Added Mass Matrix about Free Vibration of Structure in Water

Zhang Wen-peng Zong Zhi
School of Naval Architecture Engineering，Faculty of Vehicle Engineering and Mechanics，State Key Laboratory of Structural Analysis for Industrial Equipment，Dalian University of Technology，DaLian 116024，China

In analysis of ship global vibration，influence of outboard water should be considered.For studying the global vibration，two methods can be used.One is that 3D finite element model of water domain is applied，and the other is that added mass is introduced into structural matrix for calculation. With the finite element technique developing，3D finite element model of ship is usually taken.However，it is not correct for traditional method（such as Lewis added mass method）to neglect the deformation of ship transverse section.We proposed a kind of boundary element method to calculate the 3D added mass matrix of structure with 3D effect，and analyzed the wet structural response.The results show that the method is available and accuracy.

structure in water；3D added mass matrix；free vibration analysis；wet mode

U661.44

：A

：1673－3185（2011）04－13－06

2011-04-08

创新研究群体科学基金（50921001）；国家重点基础研究发展计划项目（2010CB832700）

张文鹏（1980－），男，博士研究生。研究方向：水下爆炸、流固耦合、船舶水动力学、结构振动。E-mail：zwp_ln＠163.com

宗 智（1964－），男，教授，博士生导师。研究方向：水下爆炸、流固耦合、水动力学、结构冲击、计算力学。E-mail：zongzhi＠dlut.edu.cn

10.3969/j.issn.1673-3185.2011.04.003