增升减阻流动控制技术的数值模拟研究

石 清，李 桦

(1.中国空气动力研究与发展中心，四川 绵阳 621000;2.国防科学技术大学航天与材料工程学院，湖南 长沙 410073)

0 引言

流动控制的本质是通过改变局部流动来控制流体动力的作用，它可分为两类:一类是被动控制，如微型涡流发生器、实体鼓包等;另一类是主动控制，如零净质量射流。采用被动流动控制技术，有结构简单易行等优点，但在非设计状态下往往难以达成预期的流动控制目标。运用主动流动控制技术，虽然结构相对复杂，但可以在不改变飞行器布局外形的情况下，利用致动器改变局部流动来控制飞行器绕流的流态，从而获得改善飞行器性能的效果。

机翼高效增升减阻技术是飞机优化设计的核心技术，而非定常流动被动/主动控制技术是机翼进一步增升减阻的重要措施之一。

机翼作为飞机的一个关键气动部件，增升对飞机性能有重要影响。有数据表明，起飞时，最大升力系数CLmax增加5%，有效载荷约可增加15%;着陆时，最大升力系数CLmax增加5%，有效载荷约可增加40%。

依据升力的形成机理和流动性态对机翼升力的影响，采用流动控制的手段改变翼型下翼面前缘处的局部流动，可改善翼型的压力分布，继而提高升力系数和升阻比。

典型的运输机在巡航状态时机翼阻力约占全机阻力的45%。机翼的阻力根据其不同形成机理，可分为四种阻力:由粘性空气与机翼表面摩擦而形成的摩擦阻力、由涡系引起升力倾斜而形成的亚声速诱导阻力(或超声速升致阻力)、由迎风面积而形成的压差阻力、由存在激波而形成的激波阻力。

依据阻力的形成机理和流动性态对机翼阻力的影响，可采用相应的流动控制方法来进行减阻。比如:利用层流附面层固有的低摩擦特性，尽可能延缓浸润面积上的层流附面层向湍流附面层转捩，维持较长的层流附面层的流动，或采取措施使湍流附面层转变为层流附面层，以获得较小的摩擦阻力;直接改善湍流附面层的流动形态和涡结构之间的相互作用，利用湍流附面层较强的抗分离能力，延缓附面层分离，减小因附面层分离而带来的压差阻力;减弱翼型上表面的激波强度，使总压损失减少，从而使激波阻力降低。

本文采用数值模拟方法，研究采用微型涡流发生器延迟流动分离、采用实体鼓包减弱激波强度进而实现减阻的流动被动控制机理与参数影响规律，研究采用零净质量射流控制分离涡实现增升的流动主动控制机理与参数影响规律，为我国大型飞机增升减阻气动优化设计提供了有实用价值的技术储备。

1 数值模拟方法

1.1 带微型涡流发生器的大展弦比超临界机翼的数值模拟

非定常流动、网格生成、加速收敛技术是数值模拟带微型涡流发生器大展弦比超临界机翼的主要难点。控制方程为三维非定常N-S方程，湍流模型为S-A一方程模型，采用了非定常方程的双时间步求解方法和对接拼接网格技术以及多重网格加速收敛技术。

1.2 带实体鼓包的超临界翼型的数值模拟

跨声速激波/附面层干扰、后缘发散超临界翼型边界条件的处理是数值模拟带实体鼓包的超临界翼型的主要难点。控制方程采用二维N-S方程，湍流模型分别为S-A一方程模型和SST两方程模型，采用了Van Leer分裂和LU-SGS隐式算法。

1.3 带零净质量射流的翼型的数值模拟

非定常流动、湍流计算以及边界条件的处理是对零净质量射流数值模拟的主要难点。控制方程为二维非定常N-S方程，湍流模型分别采用了S-A一方程模型和SST两方程模型，无粘通量项采用Roe的通量差分来离散，限制器分别为Van-albada限制器和Venkat限制器，粘性通量项用中心差分格式离散，非定常时间导数项的处理采用了双时间步长法。

2 算例考核

考核了五个算例。

2.1 对M6机翼的计算考核

计算条件为:M=0.8395，α =3.06°。

图1给出了单重对接、多重对接、单重拼接和多重拼接四种计算方法的结果与试验值的对比。从图可见，单重对接和多重对接的计算结果、单重拼接和多重拼接的计算结果符合较好;对接网格和拼接网格的计算结果差异较小。

2.2 对RAE2822翼型的计算考核

计算条件为:

表1为本文计算结果与试验结果的比较。从中可见，采用S-A与SST模型计算的升力偏小，SST模型计算得到的阻力偏小。

2.3 对NASA sc(2)-0714超临界翼型的计算考核

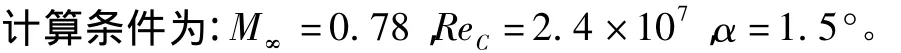
图2为等压线分布与流线分布。从图3可见，计算结果与试验结果基本相符。

2.4 对NACA0012翼型定常计算的考核

计算条件为:M∞=0.6，α =0°、2°，ReC=3 ×106。

从表2和表3可见，计算结果和实验结果相差较小，SA模型和SST模型的计算结果接近。为模拟翼型下翼面的致动器而导致计算网格不对称，使零攻角时升力有小量。

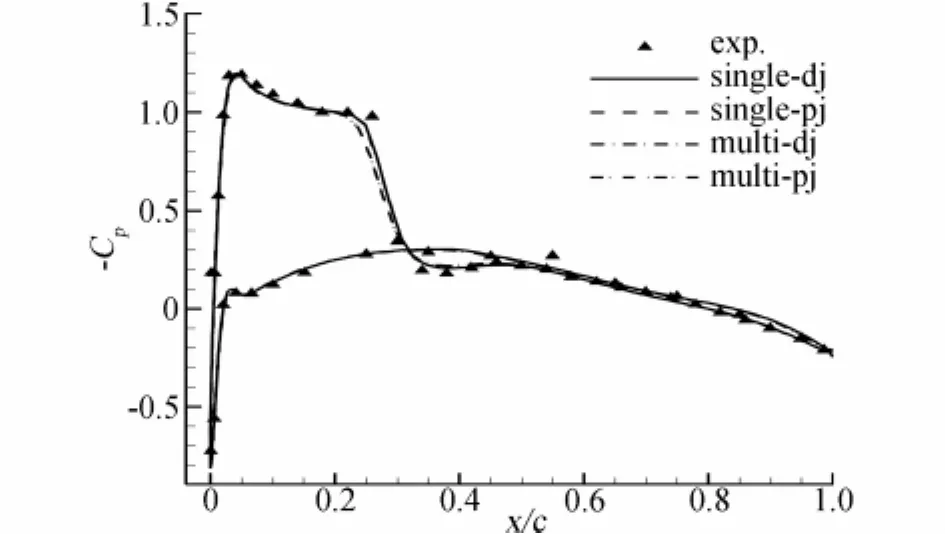
图1 机翼剖面压强系数分布对比Fig.1 Comparison of calculation and experimental results of pressure distribution

表1 RAE2822气动力计算结果与试验结果的比较Table1 Comparison of calculation and experimental results for RAE2822 aerofoil

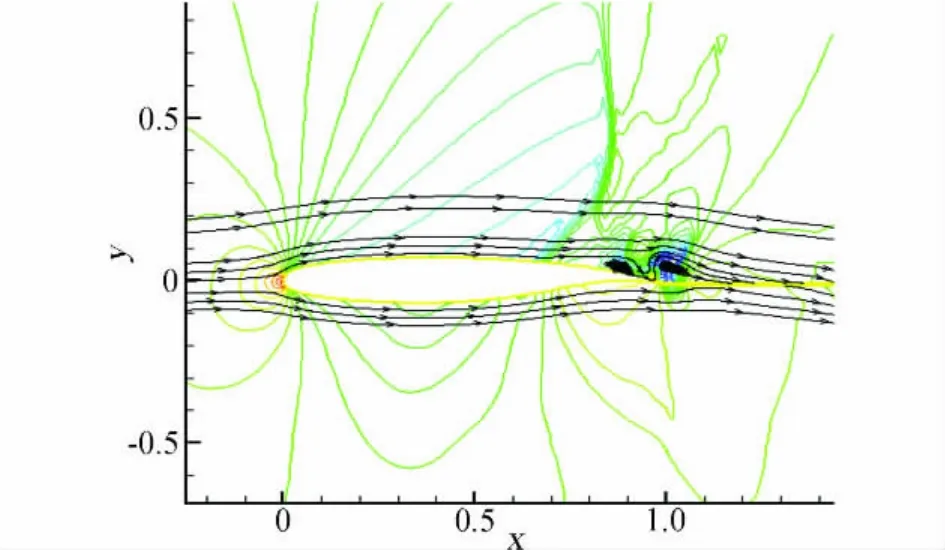
图2 等压线分布与流线分布Fig.2 The distribution of isobar and streamline

图3 压力系数分布计算结果与试验结果比较图Fig.3 Pressure distribution comparison of calculation and experimental results

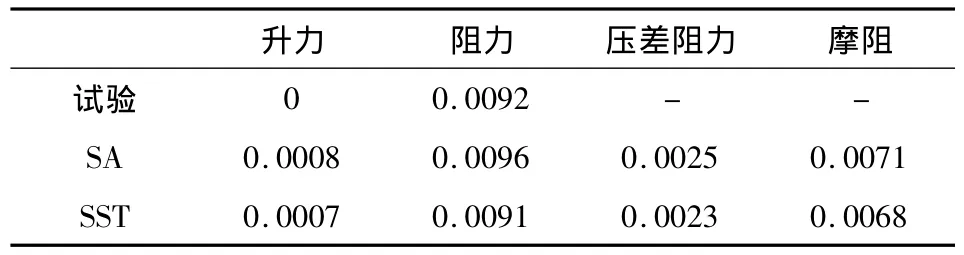
表2 无射流时0°攻角气动力系数的比较Table2 Comparison of the different aerodynamic coefficient without jet flow(α =0°)

表3 无射流时2°攻角气动力系数的比较Table3 Comparison of the different aerodynamic coefficient without jet flow(α =2°)

2.5 对NACA0012翼型非定常计算的考核

图4和图5分别是在不同时间步长时计算结果与试验结果的比较，计算的法向力、俯仰力矩与试验结果符合较好。由图可见，不同时间步长的计算结果基本一致。

3 计算外形

3.1 超临界机翼/翼身组合体及微型涡流发生器

超临界机翼翼身组合体气动力计算的参数如下:参考长度bA=0.37194m，机翼展长l=2.88m，参考面积S=0.467262m2，力矩参考点 Xm=1.755m(距机头)，Ym=1，Zm=0。翼身组合体的对接拼接网格拓扑结构如图6所示。

图4 法向力迟滞曲线Fig.4 Sluggish curve of normal force

图5 俯仰力矩迟滞曲线Fig.5 Sluggish curve of pitch moment

图6 翼身组合体网格拓扑Fig.6 The grid of combination

图7 涡流发生器形状示意图Fig.7 The sketch map of micro-vortex generators

微型涡流发生器VG的形状如图7所示，长度为L，厚度为D，高度为H。在本文算例中，δ为涡流发生器安装位置处的附面层厚度，微型涡流发生器的高度H=0.5δ、H=1.5δ分别命名为H1和H2;弦向安装位置x/c=0.30、x/c=0.40、x/c=0.50、x/c=0.65 分别命名为C1、C2、C3、C4。

图8 涡流发生器的计算网格Fig.8 The grid of micro-vortex generators

图8为涡流发生器的计算网格。在机翼0.65弦长处，沿展向以等间隔λ=20mm、相同偏角β=30°布置了15个微型涡流发生器。

3.2 超临界翼型及实体鼓包

基本翼型为NASA sc(2)-0714后缘发散的超临界翼型。

在上述基本翼型的上表面加装鼓包。鼓包长度为0.2%c，位于基本翼型的55% ～75%弦长处，最大高度分别为0.35%c和1.75%c。基本翼型及实体鼓包如图9所示。

图9 基本翼型及实体鼓包Fig.9 The basic aerofoil and the contour bump

3.3 有零净质量射流时的翼型

计算模型如图10所示，在NACA0012翼型下翼面弦长0.13c～0.23c处分布了一排致动器。假设各致动器同相，振荡速度均为:

式中，Vn为无量纲的射流速度幅值，f为无量纲频率。

图10 有零净质量射流时翼型绕流的计算模型Fig.10 Computation model with the zero mass jet flow

4 计算结果与分析

4.1 带微型涡流发生器的超临界机翼的数值模拟

4.1.1 翼身组合体中干净机翼的附面层特性

图11为M=0.2时翼身组合体升力系数随迎角的变化。小攻角时升力系数曲线的斜率不变。当迎角大于α≥8.5°时，升力系数曲线的斜率变化缓慢，表明机翼附面层出现弱分离，且分离区发展缓慢。当迎角大于α≥12°时，升力系数曲线出现拐点，表明机翼附面层出现强分离，且分离区迅速发展。

图11 翼身组合体升力系数曲线Fig.11 The curve of lift coefficient

4.1.2 涡流发生器高度对机翼流态的影响

计算状态为M=0.2，α=10.5°。涡流发生器的高度分别为H1和H2，安装涡流发生器的弦向位置为C3。

图12至图14分别为干净机翼、VG-H1-C3和VGH2-C3的上表面流线图。

比较图12与图13，在同一马赫数和迎角下，高度为H1的微型涡流发生器使机翼上表面的分离线后移。这表明高度合适的微型涡流发生器对机翼上表面的流动分离控制起着有利作用。

比较图13与图14，在相同来流条件和同一弦向安装位置下，高度为H2的微型涡流发生器使机翼上表面的分离区变大，翼面上的流动恶化。这表明当微型涡流发生器的高度超过附面层厚度时，增强了机翼上表面的流动分离。

分离流动始于壁面，源于逆压梯度的增加。分析涡流发生器控制流动分离的机理，高度合适的微型涡流发生器使附面层上部的高能气流得以与近壁面的低能气流混合，从而延迟分离。如果涡流发生器的高度过高，又将扰乱翼面上的流动，引起机翼上表面的流动分离，从而恶化机翼气动力特性。

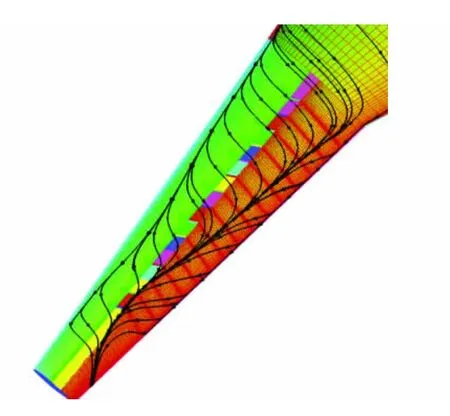
图12 干净机翼上表面流线图Fig.12 The streamline map of alone wing

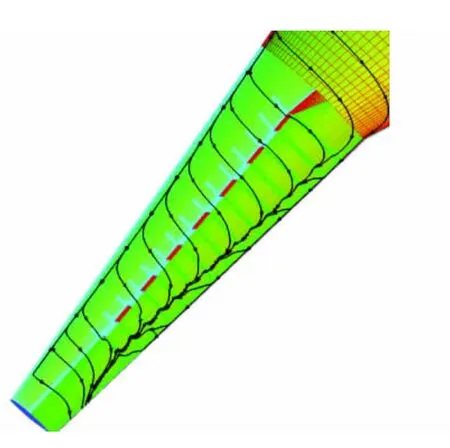
图13 VG_H1_C3的表面流线图Fig.13 The streamline map of VG_H1_C3

图14 VG_H2_C3的表面流线图Fig.14 The streamline map of VG_H2_C3

4.1.3 涡流发生器的弦向位置对机翼升阻特性的影响

计算状态为M=0.76，α=4°。涡流发生器的高度为 H1，弦向安装位置分别为 C1、C2、C3、C4。

表4为有/无涡流发生器时机翼气动力系数差值比较。从表中可见，在VG-H1-C1状态时，涡流发生器取得了增升且减阻的效果。在其它状态时，涡流发生器使升力和阻力都略有增加。这也说明，涡流发生器最佳气动效率的取得与其弦向安装位置有关。

表4 有/无涡流发生器时机翼气动力系数Table 4 Aerodynamic coefficient comparison of with/without micro-vortex generators

4.2 带鼓包的超临界翼型的数值模拟

4.2.1 基本翼型与加鼓包翼型等马赫线分布的比较

图15与图16分别为基本翼型和有鼓包翼型的马赫数等值线图，鼓包最大高度为0.35%c。由图可见，加鼓包后马赫数等值线在鼓包附近变化较大，基本翼型在此条件下的波脚大约处在x/c=0.625的位置，而加鼓包后波脚向后移动处于x/c=0.64的位置，同时鼓包弱化了上表面的激波强度，波脚的范围向前和向后扩大了，这是因为鼓包的存在，在鼓包的迎风面出现一组等熵压缩波，波前气流的流速下降，在波脚激波的强度减弱，波前波后的压差减少，这说明在激波波脚下的鼓包可以减弱激波的强度。

4.2.2 不同高度的鼓包对翼型压力系数分布的影响

图15 基本翼型等马赫数线M=0.72，Re=2.4 ×107，α=1°Fig.15 Iso Mach number line of the basic aerofoil

图16 加鼓包翼型等马赫数线M=0.72，Re=2.4 ×107，α=1°Fig.16 Iso Mach number line of the aerofoil with contour

图17为基本翼型与加0.175%c鼓包和加0.35%c鼓包的翼型表面压力系数的比较。由图可见，三种翼型的压力系数曲线在大部分区域是相同的，只有在鼓包附近压力分布不同，基本翼型的激波较陡，两个加鼓包的翼型的上表面激波的位置与基本翼型相近，但是激波的强度有不同程度的减弱，鼓包高的激波强度更弱一些。这表明鼓包可以减弱翼型上表面的激波，从而减小波阻。

图17 不同高度的鼓包对翼型压力系数分布的影响Fig.17 The effect of the contour bump height

4.2.3 鼓包对翼型气动力特性的影响

表5列出了M=0.78、鼓包最大高度为0.35%c时翼型气动力特性的比较。在迎角大于1°时，实体鼓包降低了翼型的阻力，并提高了升阻比。

表5 实体鼓包减阻效果Table5 The effect of drag reduction with contour bump

4.3 有零净质量射流时翼型绕流的数值模拟

4.3.1 射流频率对翼型升力、阻力和升阻比的影响

从表6可见，射流频率一定时，随着射流速度幅值的增加，翼型的平均升力系数和阻力系数都增加。当射流频率为1.0、射流速度幅值为0.1时，升阻比最大。

从表6还可见，在射流速度幅值一定时，射流频率对翼型升力、阻力和升阻比的影响呈非线性。

表6 不同射流速度和频率时用SA模型计算的结果比较Table6 Comparison of the computational results using SA model at different jet flow velocity and frequency

4.3.2 射流速度幅值对翼型升力的影响

图18为射流速度幅值为0.2时翼型平均升力随射流频率的变化曲线。从图可见，射流频率对翼型升力的影响呈非线性，当射流速度幅值为0.2、射流频率为1.5时，升力最大。

图18 平均升力随频率变化曲线(Vn=0.2)Fig.18 Curve of lift with frequency(Vn=0.2)

5 结论

通过对带微型涡流发生器的大展弦比超临界机翼、对带实体鼓包的超临界翼型和带零净质量射流的翼型的数值模拟，研究了流动被动/主动控制的机理和流动控制器件参数的影响规律，为我国大型飞机增升减阻气动优化设计提供了有实用价值的技术储备。得到以下结论:

(1)对数值模拟方法的考核算例表明，针对超临界翼型和超临界机翼上小尺度流动控制器件及其诱导的时空多尺度非定常粘性流动和激波/附面层干扰流场，发展了合适的数值模拟技术。

(2)采用翼面上布置涡流发生器可以控制翼表面的分离流，涡流发生器的高度应为附面层厚度量级。高度合适的微型涡流发生器对机翼上表面的流动分离起着有利的控制作用。但高度过高的涡流发生器将引起机翼上表面的流动分离，使气动力特性恶化。涡流发生器最佳气动效率的取得与其弦向安装位置有关，针对超临界机翼失速前分离弱、分离区发展缓慢的附面层分离特点，涡流发生器应安装于附面层分离线前面不远处。

(3)在中高升力系数情况下，采用实体鼓包可明显提高翼型的升阻比。随着鼓包高度的增加，在鼓包发挥有利作用的范围内减阻效果增强。

(4)随着射流速度幅值的增加，翼型的平均升力系数和阻力系数都要增加。射流频率对翼型升力的影响呈非线性。

［1］倪亚琴.涡流发生器研制及其对附面层的影响研究［J］.空气动力学学报，1995，13(1):110-116.

［2］JOHN C L.Review of research on low-profile vortex generators to controlboundary layer separation［J］.Progress in Aerospace Science，2002，38:389-420.

［3］BRAGG M B.Experimental study of airfoil performance with vortex generators［J］.Journal of Aircraft，1987，24(5):305-310.

［4］BROADLEY I.Effectiveness of vortex generator position and orientation on highly sweptwings［R］.AIAA paper 97-2319.

［5］RAE A J.Investigation into scale effects on the performance of sub boundary-layer vortex generators on civil aircraft highlift devices［R］.AIAA Paper 2002-3274.

［6］LIN J C.Small submerged vortex generators for turbulent flow separation control［J］.Journal of Spacecraft，1990，27(5):503-507.

［7］JOHN C L.Control of turbulence boundary layer separation using micro-vortex generators［R］.AIAA 99-3404.

［8］RIVERS M B，WAHLS R A.Comparison of computational and experimental results for a supercritical aairfoil［R］.NASA TM-4601.

［9］SETTLES G S，WILLIAMS D R，BACA B K，BOGDONOFF S M.Reattachment of a compressible turbulent free shear layer［J］.AIAA Journal，1982，20(1):60-67.

［10］BARRETT B，HARVARD L.Thin-layer approximation and algebraic model for separated turbulent flows［R］.AIAA 78-257.

［11］LONDENBERG W K.Turblence model evaluation for the prediction offlows over supercritical airfoil with deflected aileron at high reynolds number［R］.AIAA-93-0191.

［12］HENNE P A，GREGG R D.New airfoil design concept［R］.AIAA Paper 89-2201.

［13］陶洋.实体鼓包改进超临界翼型跨声速气动特性研究［J］.空气动力学学报，2007，25(1):116-119.

［14］HASSAN A A.Application of zero-net-mass jets for enhanced rotorcraft aerodynamic performance［J］.AIAA Journal，2001，28(3):478-485.

［15］TANG H，ZHONG S.Incompressible flow model of synthetic jet actuators［J］.AIAA Journal，2006，44(4):908-912.

［16］DUBUC L，etal.Solution ofthe unsteady euler equations using an implicit dual-time method［J］.AIAA Journal，1998，36(8):1417-1424.

［17］YOON S，JAMESON A.Lower-upper symmetric-Gauss-Seidel method for the Euler and Navier-Stokes equations［J］.AIAA Journal，1988，26(9):1025-1026.

［18］MENTER F.Zonal two equation turbulence models for aerodynamic flows［R］.AIAA 93-2906，1993.

［19］KRAL L D，DONOVAN J F.Numerical simulation of synthetic jet actuators［R］.AIAA 97-1824，1997.

［20］高峰，汪亮.微射流作动器三维外流流场数值模拟［J］.空气动力学学报，2003，21(2):244-249.

［21］肖中云，牟斌，陈作斌.零质量射流与分离控制的数值模拟［J］.空气动力学学报，2006，24(1):46-50.