γ-Reθ转捩模型的标定研究

张玉伦，王光学，孟德虹，王运涛

(中国空气动力研究与发展中心空气动力学国家重点实验室，四川 绵阳 621000)

0 引言

随着飞行器性能越来越高，工程上对气动力数据的精度要求也越来越高。由于边界层转捩对摩擦阻力、流动的分离位置等有很大的影响，因此对边界层转捩位置的准确模拟就成为一个非常重要的工程问题。特别在中等雷诺数范围，层流区域和湍流区域具有相同的量级时，使用全层流或全湍流计算方法都会导致很大的计算误差，对转捩位置的模拟就更显得必要。

转捩的机制非常复杂，比如有自然转捩(由T-S波或横向流失稳造成)、旁路转捩(自由流中的高水平湍流度/扰动施加在层流边界层上造成)、分离诱导转捩以及湍流在顺压梯度区的再层流化等，使得转捩的模拟非常困难。虽然NS方程具有模拟转捩过程的能力，而且随着计算机的发展，近年来湍流的高级数值模拟方法，如直接数值模拟(DNS)和大涡模拟(LES)得到了很大发展，也取得了许多令人满意的结果，但是距离工程实用还有很长的距离。在工程应用中，转捩主要靠经验或半经验的方法来确定，比如经验关联方法、eN方法和低雷诺数湍流模型方法等。

经验关联方法就是把自由流的湍流度和当地的压力梯度等通过试验数据关联到转捩动量厚度雷诺数。典型的关联如Abu-Ghannam和Shaw的关联。然后，通过比较实际的和关联的动量厚度雷诺数来确定转捩的起始位置。由于要计算非局部变量-动量厚度，该方法难以与现代CFD方法相匹配，特别对于非结构网格和并行计算，问题更突出。

eN方法亦称为线性稳定性分析方法，是基于线性稳定性理论和试验数据的半经验方法。该方法假设:转捩过程是由层流边界层内最初的小扰动向下游传播放大达到eN时完成。此法归结为确定放大因子N，所以N值就成了判断转捩的准则。由于eN方法本身没有解决如何选取N值，也没有考虑环境条件对转捩的影响，因而在实际应用中是靠低湍流度试验来确定N的。但是eN方法难以处理旁路转捩和推广到三维情况。

低雷诺数湍流模型适用于三维流动，也能够与现代CFD方法相匹配，但是该方法不能模拟旁路转捩，模拟自然转捩的能力也受到质疑，这是因为，低雷诺数湍流模型中阻尼函数的标定依据是再现粘性底层的行为，而不是从层流到湍流的转捩。

还有一类基于间歇因子γ的转捩预测方法。间歇因子被定义为空间某点的流态是湍流的概率，是Dhawan＆Narasimha［1］首先引入的。之后出现了大量的间歇因子的转捩预测方法，例如:Cho＆Chung［2］针对自由剪切流发展了与k-ε湍流模型联合使用的间歇因子输运方程方法，Steelant＆Dick［3］发展了与条件平均 NS方程联合使用的间歇因子输运方程方法，Suzen＆Huang［4］将 Steelant＆ Dick 的模型与 Cho ＆ Chung 的模型相结合发展了间歇因子的对流-扩散方程。但是所有这些转捩模型都需要积分动量厚度，难以与现代CFD方法相匹配。

为了适应现代 CFD 计算，Menter＆Langtry［5］提出了基于当地关联的γ-Reθ转捩模型(local correlation-based transition modeling，LCTM)。该模型把经验关联方法和间歇因子方法有机地结合了起来，通过经验关联函数-转捩动量厚度雷诺数来控制边界层内间歇因子的生成，再通过间歇因子来控制湍流模型中湍流的生成。该模型通过把动量厚度雷诺数与当地的最大应变率(或涡量)相关联，回避了动量厚度的计算，又通过Reθ输运方程回避了经验关联函数的非当地计算，从而实现了模型计算的当地化。该模型并不试图模拟边界层内转捩的物理过程，只是为把经验关联方法融入到现代CFD中去提供一个有效途径。该模型的特点是:1)可以使用不同的经验关联函数进行标定;2)能够涵盖不同的转捩机制;3)不依赖初场，即无论初始边界层是层流还是湍流，都有相同的解;4)不影响基础湍流模型在完全湍流区的行为;5)不依赖坐标系的选取;6)适用于三维边界层流动。因此，该模型取得了很大的成功。但是，该方法要用到几个经验关联函数，由于模型的标定对所使用的CFD软件平台的差异是敏感的，所以，这些关联函数在不同的CFD软件平台之间缺乏互换性。

本文的主要工作就是补充了相应的关联函数，基于平板的试验数据在CARDC的trip软件平台上进行了标定，并研究了关联函数的变化对转捩结果的影响规律。

1 γ-Reθ转捩模型简介

两方程转捩模型的最终目的是求解间歇函数 (即空间某点的流态是湍流的概率，0≤γ≤1)，并通过它与湍流模型的联合来控制转捩的发生。无量纲的输运方程［5］的守恒形式为:

上式中的S为应变率的模，Ω为涡量的模，y为离壁面的最小距离，Flength是转捩区的长度，Reθc是边界层内间歇函数开始增加位置的临界动量厚度雷诺数。Flength和Reθc是经验关联函数，它们都是转捩动量厚度雷诺数Reθt的函数。转捩雷诺数Reθt是边界层外自由流湍流度Tu、流向压力梯度参数λθ等的函数。

对于关联函数Reθt，不同文献中的形式略有不同，本文采用Langtry［6］建议的形式:

其中U是当地的速度，θ是动量厚度，s为流线的弧长。F(λθ)代表了压力梯度的影响。在上式中，Reθt是用当地的湍流度Tu和压力梯度参数λθ计算的，直接用到边界层内显然不符合实际，为了解决这个问题，Menter等专门使用了一个输运方程，即～Reθt方程。使得边界层以外的 ～Reθt通过经验关联 Reθt获得，边界层之内的～Reθt通过输运方程从边界层以外的 ～Reθt扩散而来。～Reθt输运方程［5］:

源项Pθt的设计目标就是使边界层以外的等于Reθt，所以式子中有个(Reθt-)。混合函数 Fθt用来关掉边界层内的生成项Pθt从而使得从边界层以外扩散得到，所以设计Fθt的原则是在边界层以外(即自由流)Fθt=0而在边界层内 Fθt=1.0;Fwake的作用是保证混合函数Fθt在尾迹区不被激活。

为了模拟分离诱导转捩，对间歇函数γ进行如下修正［5］:

该转捩模型只是获得间歇函数γ，还需要与湍流模型联合才能模拟转捩过程。Menter采用的湍流模型为SST模型。具体的联合方式就是使用间歇函数γ来修正k方程的生成项、破坏项和混合函数［5］，即:

其中:Pk，Dk和Florig是SST模型中原来的生成项、破坏项和混合函数，Menter推荐的γDkmin=0.1;对ω方程不做修正。

上述方程使用的无量纲化参数见表1。

表1 参数无量纲化表Table1 Parameter dimension

2 关联函数的选择和标定

标定工作在CARDC自行开发的trip软件平台上进行。对流项的离散选用MUSCL_roe格式，耗散项的离散采用二阶中心格式，离散方程采用LU-SGS方法求解，为了适应低速情况和加速收敛，采用了预处理技术和多重网格技术。

标定依据文献［5］提供的 T3A、T3B、T3A-和 Schubauer＆Klebanof等平板试验数据，试验条件见表2。

表2 平板转捩试验的进口条件Table2 Inlet condition for the flat plate test cases

计算网格如图1，平板长度为2.0，来流远场边界距平板前缘0.22，法向远场边界距壁面也是0.22，网格为H型，壁面上第一层网格的法向距离1.0×10-6，平板前缘第一网格的x向距离1.5×10-3。网格规模为425×129，其中壁面上有392网格点。

图1 平板的计算网格Fig.1 computational mesh for flat plate

该转捩模型经由关联函数Reθt强烈依赖当地自由流湍流度，只有正确模拟了自由流湍流度，标定工作才有意义。由于在进口处指定的湍流度会迅速衰减，而且进口涡粘性比(μt/μ)越小，湍流度衰减越快，可是，如果进口涡粘性比给的太大，壁面摩阻又会偏离层流太多，所以应该认真指定进口湍流度和进口涡粘性比，以保证平板前缘自由流湍流度有正确的值和期望的衰减率。在自由流中，湍动能的衰减可以根据下式［7］计算

其中 β=0.09，β*=0.0828，t=x/V为时间，x是下游距进口的流向距离，V是平均速度。使用湍流度和涡粘性比(μ1/μ)，可以将上述湍动能的衰减规律重新写成:

图2给出了各种情况下边界层外自由流湍流度的衰减与试验的比较，计算与试验吻合。

关联函数Flength和Reθc并不是相互独立的，形式也不是固定的。为了便于确定他们，本文采取先给定其中的一个(Reθc)，然后通过平板的试验数据来确定另一个(Flength)。同时，为了能够在校验中有灵活而足够的自由度，Flength的形式采用样条拟合曲线。

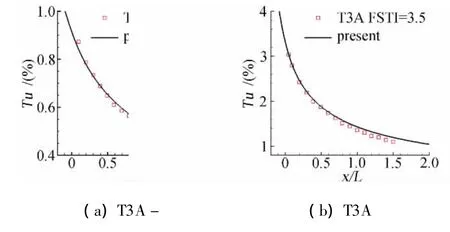
图2 自由流湍流度衰减与试验的比较Fig.2 Comparison of free stream turbulence decay between CFD calculations and wind tunnel data

尽管该模型对转捩过程有一定的模拟能力，但毕竟转捩过程是复杂的，而且对于大部分雷诺数比较高的航空问题，能够正确模拟转捩位置就基本能够满足工程需求了，所以本文中关联函数的标定主要依据转捩位置，适当兼顾转捩区长度。同时，虽然Flength被称之为转捩区的长度，实际上这种叫法并不准确。比如，如果固定Reθt和 Reθc，那么增加 Flength，转捩区确实会加长，但此时转捩位置也会提前;如果要保持转捩位置不变，那么增加 Flength，就要相应增加 Reθc(固定 Reθt)，此时转捩区反而会变短。也就是说，在保持转捩位置不变的前提下，改变 Reθc就会改变转捩区长度。因此，在本文中 Reθc的选择主要依据转捩区长度，相反，Flength的确定则只依据转捩位置。

通过分析不同文献的计算结果，我们发现:为了尽可能模拟转捩区长度，相对于，关联函数 Reθc在低区要尽可能大(≈1)，而在高 ～Reθt区则要适当的小。因此，本文选择如下形式的:

其中Cθc是一个常数，用来控制 Reθc的大小。为了考察不同 Reθc的影响，本文分别考察了 Cθc=0.15、0.24、0.33三种情况，对应的 Reθc～如图3所示。标定后的关联函数Flength拟合曲线如图4所示。如图5给出了在标定点上计算的壁面摩擦阻力系数与试验的比较。

图 3 Reθc ～Fig.3 Reθc ～

图4 F length～ Fig.4 F length ～

图5 壁面摩擦阻力系数与试验的比较Fig.5 Comparisons of skin friction coefficient distribution between CFD calculations and wind tunnel tests

从图3～图6示结果可以看出:对于给定的Reθt，要保持转捩位置不变，Reθc减小，Flength也要相应减小(见图3 和图 4)。同时，增大 Cθc即减小 Reθc和 Flength，转捩区会变宽，转捩区后的壁面摩阻会减小(见图5)，好在对摩阻的这种影响在一段距离后会消失。另外，Reθc和Flength过大(即Cθc过小)会导致计算收敛性变差，如图6所示。

还可以看出:对于来流湍流度比较低的Schubauer＆ Klebanof和T3A-两种情况(对应于较高的Reθt)，计算的转捩区比试验的窄，而转捩区后的壁面摩阻比试验的小，要增加转捩区宽度，就要减小Reθc和Flength，这样就会导致转捩区后的壁面摩阻更小，因此对于来流湍流度比较低的情况，Cθc既不能太大也不能太小。对于来流湍流度较高的T3A和T3B两种情况(对应于较低的Reθt)，计算的转捩区比试验的还宽些，但是，此时(～Reθt＜200)，Reθc几乎已经达到最大(Reθc≈0.99～Reθt)，不可能通过进一步增大Reθc来减小转捩区宽度。同时对于来流湍流度较高的情况，Cθc的变化对 Reθc几乎没有影响。下面的讨论就只是针对Cθc=0.24的情况，相应Flength样条曲线的控制点列于表3。

图6 不同的Reθc收敛情况比较(T3A-FSTI=0.87)Fig.6 Comparisons of convergencefor for different Reθc

图7给出了间歇函数γ分布云图，从图中可以清楚看出间歇函数在层流边界层中增长直到转捩的情况。图8给出了在转捩前的不同x位置转捩尺度～Reθt在边界层附近沿法向的分布，可以看出自由流中的Reθt向边界层内部扩散影响的情况，边界层内的～Reθt与自由流中的Reθt存在某种滞后。

在标定过程中发现，转捩位置以后的壁面摩阻偏小，说明转捩后边界层内的湍动能耗散过大，这主要是对湍动能方程进行修正时使用γD1min造成的。可是，如果取消γD1min，又会造成在高自由流湍流度的情况下转捩前的壁面摩阻偏离层流太多。为此，本文把上述常量γDkmin修正为可变的，以消除其对转捩后壁面摩阻的影响，同时又能保证转捩前壁面摩阻的性质。

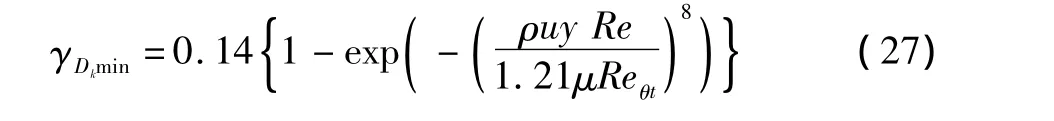
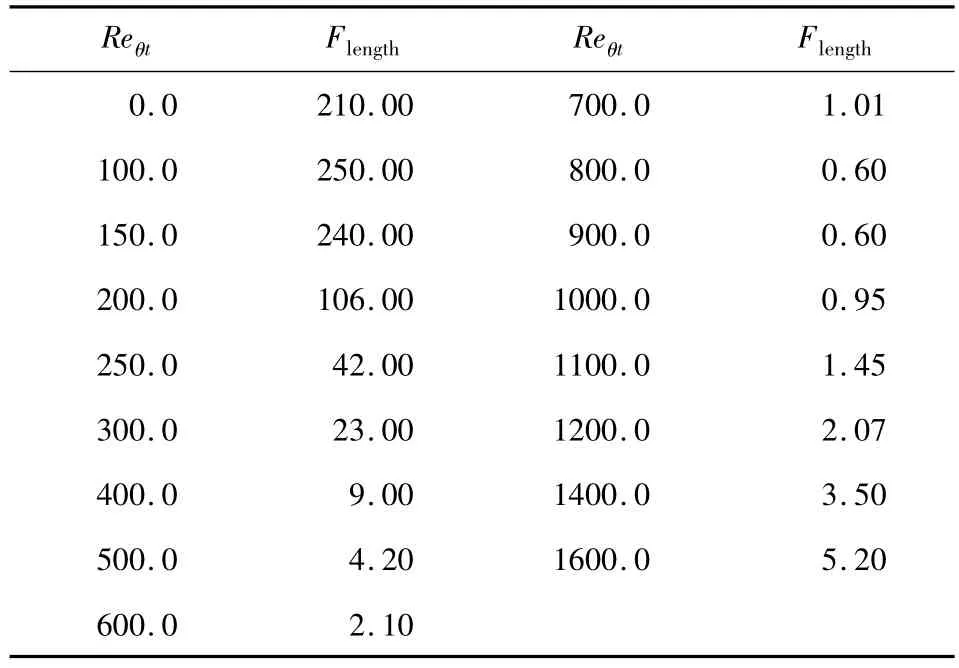
表3 样条曲线的控制点列表(Cθc=0.24)Table3 Control point of spline curve(Cθc=0.24)

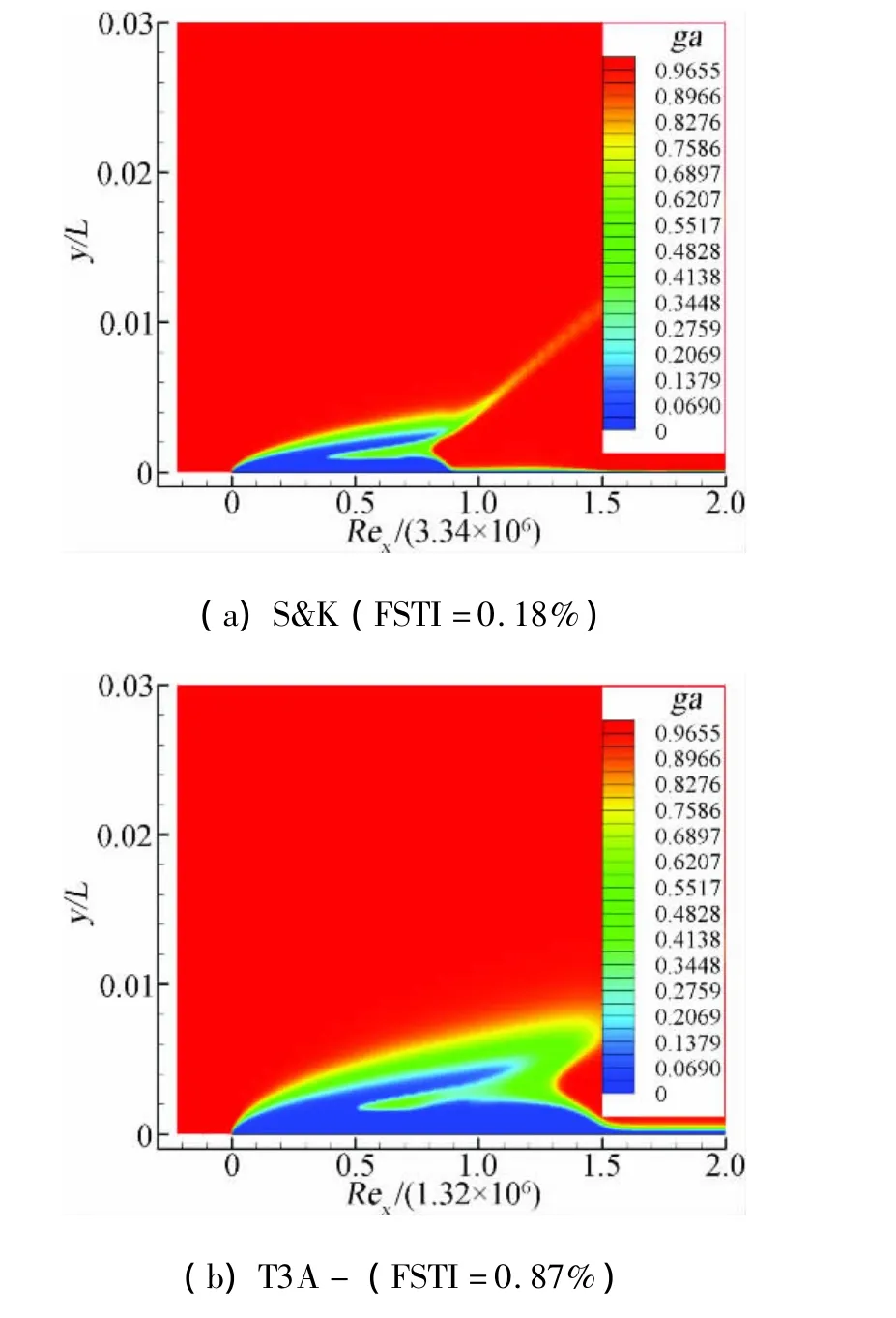
图7 间歇函数γ云图Fig.7 Contours of Intermittencyγ

图8 转捩前边界层附近转捩尺度～Reθt的分布Fig.8 Profiles of the～Reθt for a flat plate

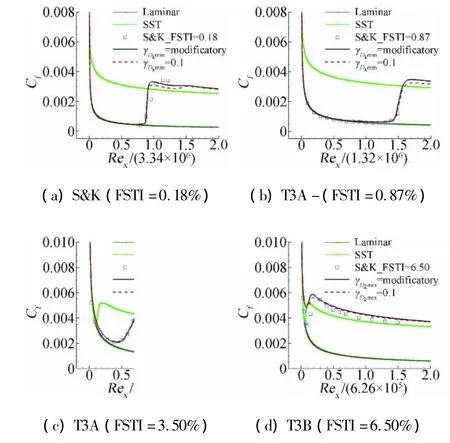
图9 γDkmin有∕无修正时壁面摩阻的比较Fig.9 Comparisons of skin friction coefficient distribution between modified and nomodifiedγDkmin

图9给出了修正前后壁面摩阻的比较，表明修正取得了满意的效果。

当然，使用四个试验点来标定关联函数实在太过勉强。比如，图10给出的两条Flength～曲线在标定点上是重合的，数值试验也表明这两个关联函数Flength在四个标定点上给出了相同的转捩位置，但是，偏离标定点之后，二者给出的转捩位置就有比较大的差异。所以，要使该模型达到实用的程度，还需要更多的试验点来完善关联函数Flength。这也是关联函数Flength采用样条形式的原因。

图10 F length～ Fig.10 F length ～

3 结论

关联函数Flength和Reθc不是相互独立的，形式也不是固定的。对于给定的 Reθc，要保持转捩位置不变，Reθc和Flength要同时减小或增大。Reθc和Flength减小，转捩区会变宽，转捩位置后的壁面摩阻会减小。

Reθc和 Flength过大会导致收敛性变差。

本文对γDkmin的修正有效地改进了转捩位置后壁面摩阻偏小的状况。

［1］DHAWAN S，NARASIMHA R.Some properties of boundary layer flow during transition from laminar to turbulent motion［J］.Journal of Fluid Mechanics，1958，3(4):418-436.

［2］CHO J R，CHUNG M K.A equation turbulence model［J］.Journal of Fluid Mechanics，1992，237:301-322.

［3］STEELANT J，DICK E.Modelling of bypass transition with conditioned Navier-Stokes equations coupled to an intermittency transport equation［J］.International Journal for Numerical Methods in Fluids，1996，23:193-220.

［4］SUZEN Y，HUANG P.Modeling of flow transition using an intermittency transport equation［J］.Journal of Fluids and Engineering，2000，122(2):273-284.

［5］MENTER F R，LANGTRY R B，LIKKI S R，SUZEN Y B，HUANG P G，VÖLKER S.A correlation based transition model using local variables:part I-model formulation［R］.ASME-GT 2004-53452.Proceedings of ASME Turbo Expo 2004.Vienna，Austria，2004.

［6］LANGTRY R B.A correlation-based transition model using local variables for unstructured parallelized cfd codes［D］.［Ph.D.Thesis］.Stuttgart，2006.

［7］NIELS N SØRENSEN.CFD modeling of laminar-turbulent transition for airfoils and rotors using the Model［R］.AIAA Paper 2008-7323.

［8］LANGTRY R B，MENTER F R.Transition modeling for general cfd applications in aeronautics［R］.AIAA Paper 2005-0522.

［9］MISAKA T，OBAYASHI S.Application of correlation-based transition models to flows around wings［R］.AIAA Paper 2006-918.

［10］PETTERSSON K，CRIPPA S.Implementation and verification of a correlation based transition prediction method［R］.AIAA Paper 2008-4401.