翼型表面结冰准定常数值模拟

常士楠，杨秋明，李 延

(北京航空航天大学航空科学与工程学院，北京 100191)

0 引言

飞机在结冰气象条件下飞行时会发生结冰现象。飞机机翼表面前缘形成的冰层会改变机翼的气动外形，恶化机翼的气动特性，导致升力减小、阻力增大、失速迎角减小、力矩特性变差，严重危及整架飞机的飞行安全。因此对机翼的结冰问题进行深入研究非常必要。欧美和前苏联的相关研究机构对飞机结冰问题进行了长期而大量的细致研究，在试验研究和数值模拟方面都取得了丰硕成果。特别是近年来随着计算流体力学(CFD)技术的发展，通过数值模拟手段对结冰过程和结冰后气动特性进行数值预测成为广大研究者关注的热点问题［1-2］。虽然国内对机翼结冰问题的研究起步较晚，但是近年来越来越多的学者开始从事这方面的工作，也取得了不少成果:南航张大林提出一种边界移动技术来模拟翼型表面霜冰的生长过程［3］，西工大李凤蔚研究了时间步长和网格数对冰形的影响［4］，空气动力研究与发展中心的朱国林和易贤对二维、三维外形的机翼前缘积冰进行了数值模拟，同时对积冰试验相似准则进行了研究［5］。

对冰形进行准确预测的难点在于翼型表面产生一定厚度的冰层后壁面边界条件发生变化，网格、外流场、水滴撞击特性都将随之改变。本文利用Fluent流体计算商业软件中的动网格技术对翼型表面结冰的整个过程进行了模拟，在每个时间步长内完成网格随着壁面边界的移动而更新、周围流场和水滴撞击特性的重新计算、结冰冰形计算及壁面边界的重构工作，如此循环直至所需的结冰时间，得到最终的冰形。本文的计算方法和程序适用于对各种冰形的模拟。

1 流场计算

1.1 网格划分

网格生成是对流场进行数值计算的基础，本文以NACA0012翼型为例，根据Fluent软件中动网格功能的要求和结冰实际情况采用非结构化的三角形网格，便于对网格的局部重构和光顺，翼型壁面附近特别是前缘部分网格密度增大用来捕捉附面层区域的流动信息，网格节点数为111816，网格单元数为188738，网格划分如图1所示:

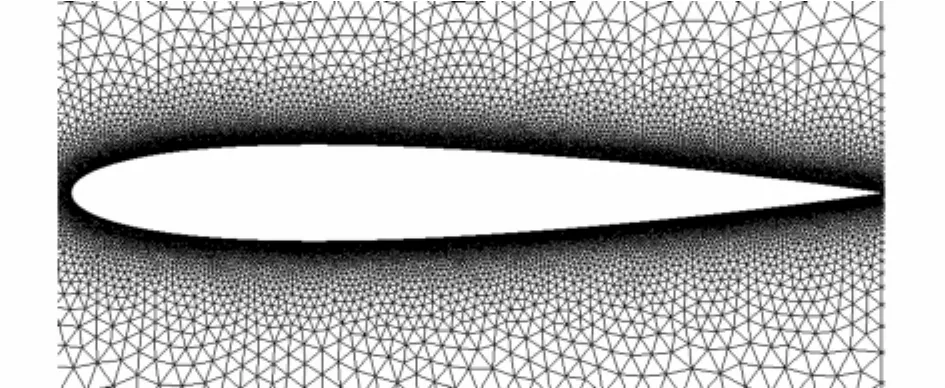
图1 NACA0012翼型网格示意图Fig.1 Diagram of grid around NACA0012 airfoil

1.2 流场计算

根据质量、动量、能量三大守恒关系建立二维非定常Navier-Stokes方程，针对某一控制体Ω写成如下积分形式［4］:

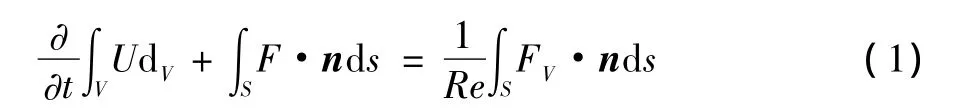
式中V为微元控制体，U为质量、动量和能量各守恒变量，s为翼型的壁面边界，F为无粘通量，Fv为粘性通量，n为控制体的外法线向量，Re为翼型的特征雷诺数。

1.3 水滴撞击特性

局部收集系数是结冰模拟过程中的一个重要参数，本文采用拉格朗日轨迹追踪法通过求解水滴运动方程来跟踪各个水滴的运动轨迹，进而确定机翼壁面上局部收集系数的分布。由于空气中液态水含量在克量级，水滴的平均容积直径在微米量级，因此可作如下合理假设［6］:(1)水滴在运动过程中和空气不发生热交换、不蒸发，水滴的物性参数不变化;(2)水滴在运动过程中不凝结、不破碎、不变形;(3)空气中水滴的存在不影响空气的流动，空气的紊流和脉动不影响水滴的运动，水滴的初速度与自由来流的速度相等。

作用在水滴上的力仅有粘性阻力、重力和空气浮力，根据牛顿第二定律，水滴轨迹运动方程可写为:

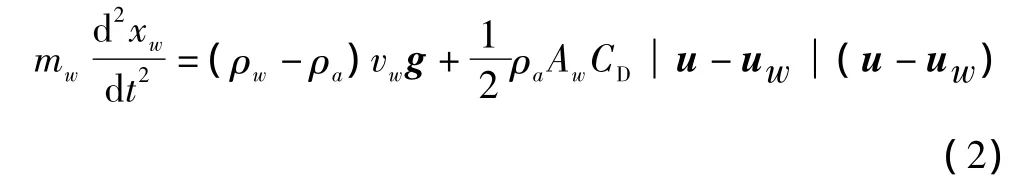
水滴的运动方程可改写为:

式中，d为水滴直径。

将前面流场速度分布的计算结果作为初始条件，上式的求解可看成一个一阶常微分方程的初值问题，因此采用四步Runge-Kutta法求解。得到各个水滴的轨迹后就可确定翼型壁面各控制体上的局部收集系数。

从光洁翼型开始到每隔单个时间步长翼型周围的流场计算结束后，都要采用上述方法计算局部收集系数的分布，这样才能体现出结冰后壁面边界变化对局部收集系数分布的影响。

1.4 对流换热系数的计算

翼型表面的对流换热系数对最终的冰形具有重要影响。传统的计算对流换热系数的方法有雷诺比拟［8］和光表面的边界层积分法［5］。虽然这两种方法使用简单，但没有考虑结冰后翼型表面粗糙度对对流换热系数的影响，与实际情况有明显差异。本文采用Kays和Crawford提出的考虑粗糙度的积分边界层法计算对流换热系数［9］，与实际的结冰情况更加接近。

目前对结冰翼型表面粗糙度形成的机理还不清楚，粗糙度分布又非常复杂，因此很难进行精确模拟。本文采用等效的沙粒粗糙度来考虑粗糙度对积冰过程特别是对流换热系数的影响［10］。等效沙粒粗糙度高度ks的计算公式为:

其中LWC为液态水含量(g/m3)，T∞为环境温度，V∞为飞行速度，c为翼型的弦长。

1.4.1 层流区域

在层流区域，局部位置的斯坦顿数［3］可用下式表示:

其中 Ge为边界层边缘的质量流速，Ge=ρUe;C1、C2、C3是与 Pr相关的函数，Pr取常数0.72，C1取0.41，C2取0.44，C3取 1.88［11］。根据 Chilton-Colburn［9］分析，结冰表面对流换热系数为:

式中ρa为空气密度，cpa为空气比热，ue为边界层边缘速度，定义为99%的来流速度，St为无量纲斯坦顿数。

根据上式可推得层流区域的局部对流换热系数:

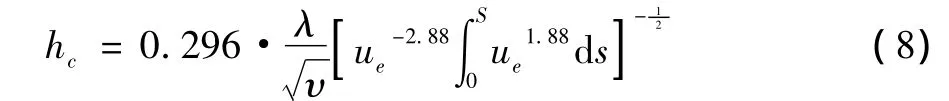
式中λ为空气的导热系数，υ为空气的运动粘度。

1.4.2 层流到湍流过渡位置的确定

本文在考虑粗糙度因素的影响时，采用Von Doen hoff和Horton［12］的标准，即满足粗糙度临界雷诺数

时，流动边界层处于湍流区域。式中uk为y=ks处的速度，ks为等效沙粒粗糙高度［8］。而根据文献［9］可知:

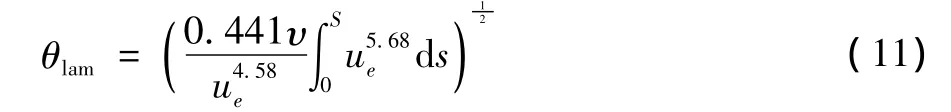
1.4.3 湍流区域

同层流区域情况类似，首先求出边界层局部位置的斯坦顿数，是等效砂粒粗糙度、剪力速度、摩擦系数和空气参数的函数。即:

其中，湍流普朗特数Prt取常数值0.9，Pr为0.72。式中Stk为无量纲粗糙度斯坦顿数:

式中C1取常数值1.0［14］，u为剪力速度，不同文献采用不同表达式，本文采用Kays及 Crawford［9］中表达式:

式中Cf为边界层区域局部位置的摩擦系数，Cf的表达式为［5］:

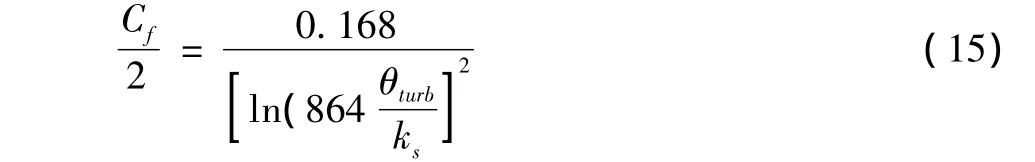
θturb为湍流边界层的动量厚度:

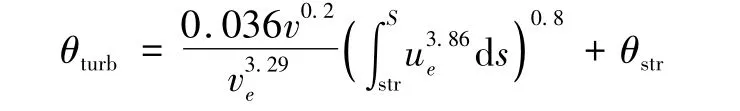
式中str是指壁面上驻点到转捩点的弧长，θstr是指转捩点处层流边界层的动量厚度。

由此可得到无量纲粗糙度斯坦顿数Stk:

将上式带入St的表达式并简化，得:

则边界层湍流区域的局部对流换热系数的表达式可表示为:

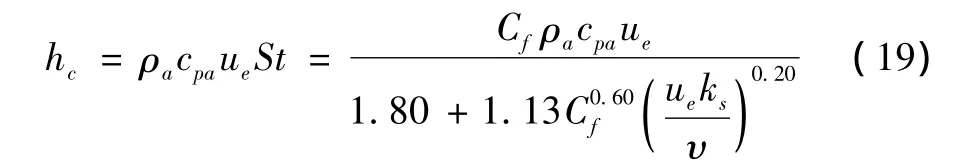
每次流场重新计算后都要用上述方法重新计算对流换热系数的分布，为下一步结冰热力学模型的求解奠定基础。

完成每个时间步长的结冰计算后都需要在壁面边界移动后新生成的计算域内重复上述流场计算、水滴撞击特性计算和对流换热系数计算。利用重新计算得到的上述结果进行下一个时间步长内的结冰计算直到完成整个结冰时间内的结冰过程的模拟。

2 结冰过程的数值模拟

2.1 Messinger积冰热力学模型

目前对结冰问题的研究大都采用经典的Messinger结冰热力学模型［15］，其基本思想是:选取结冰前机翼表面和已结冰后积冰表面的微元体为控制体，并假设为准定常过程来建立质量守恒和能量守恒方程，质量守恒方程中包含撞击水滴的质量流、流入控制体水的质量流、表面蒸发水的质量流、冻结为冰的质量流和流出控制体的质量流，能量守恒方程中包含撞击到表面的过冷水滴的能量mimiw，T、流入控制体的水滴的能量 miniw，sur(i-1)、流出控制体的水滴的能量moutiw，sur、蒸发水的能量 mevaiv，sur、冻结水的能量 mfizii，sur、气流与积冰表面对流换热释放的能量qcΔs和控制体底部与壁面的导热能量qcΔs，Δs为控制体的换热面积。由质量守恒和能量守恒关系分别建立方程:

控制体的质量守恒和能量守恒关系具体见参考文献［16］。

2.2 结冰热力学模型的求解

为了便于求解Messinger结冰热力学模型，引入冻结系数f，它表示每个控制体中结冰水的质量与控制体总共收集水质量的比值:

联立质量方程和能量方程，并将f带入可得:

各物理参数的具体意义详见文献［17］，将各参数的表达式带入式(23)后最终化简为含有表面温度ts(℃)和冻结系数f的不定方程。需要增加由结冰过程中实际物理意义的约束条件进行迭代求解。

2.3 壁面边界重构与光顺

得到各控制体的结冰质量mfrz后，可计算出每个时间步长内各控制体冰层的生长高度Δh:

根据冰层始终沿壁面外法线方向生长的假定，对翼型结冰后的壁面网格进行重构，

根据各控制体冰层生长的高度和方向，将壁面上结冰区域的网格节点进行移动，设定网格单元的最小面积Smin，当与移动节点相关的网格单元面积小于Smin时就与相邻网格单元合并，这样可以保证网格移动过程中三角形网格的畸变率不会增大，网格的质量不会下降。这样处理，只需要将壁面上结冰区域的节点和网格单元进行移动和重构，翼型后缘无冰生成的区域和远场区域的网格不需要变化，因此可以避免对单个结冰时间结束后翼型边界发生变化后的整个流场计算区域重新生成网格，提高效率。

冰层沿壁面外法线方向生长可以得到结冰时间步长后壁面各节点的新坐标，但壁面上曲率变化剧烈的区域就会导致移动后的节点光滑性变差，甚至出现相互交错的情况，严重影响网格质量，因此在进行动网格过程之前需要在保持总结冰量不变的基础上对壁面上移动后的节点进行光顺。从驻点开始，分别遍历上下壁面上的节点，三个节点编号为i-1、i、i+1，每3个节点总能组成一个三角形或者形成一条直线，以i为顶点的夹角大于设定值时，则需将节点i进行光顺。光顺后节点i的新坐标为:

对各节点的光顺需要遍历多次，确保每个节点至少有一次作为顶点被光顺过，同时要将驻点节点作为顶点进行光顺，确保上下壁面的光滑连接。根据网格节点的疏密程度，本文中夹角的设定值取150°。图2是结冰时间为360s时经过重构与光顺后的网格示意图。

通过以上所述方法对壁面节点、网格的重构和光顺，可以保证冰形轮廓不失真，提高网格质量，同时避免了对结冰后翼型边界发生变化后的流场计算区域重新生成网格。完成网格的重构和光顺后，进行下一个时间步长的流场计算、水滴撞击特性计算和结冰热力学模型的求解，如此循环直至所需要的总的结冰时间。

3 算例分析

为了便于与冰风洞实验结果比较，本文以NACA 0012翼型为例，分别模拟了环境温度为 -6.1℃、-28.4℃和-13.4℃的三种典型冰形，计算条件如下:

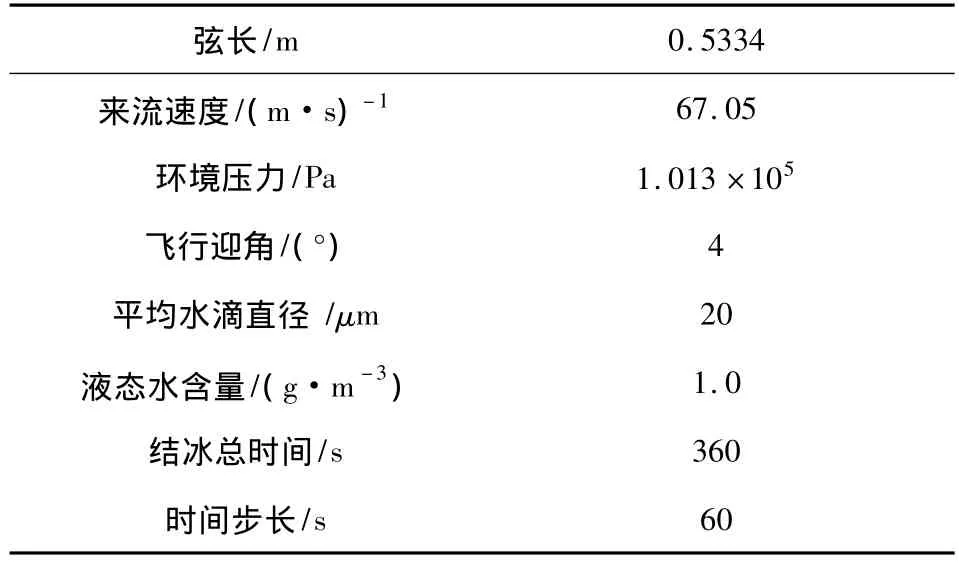
表1 飞行条件和气象参数表Table1 Flight condition and air parameter

图3、图4和图5分别表示环境静温为-6.1℃时，结冰时间步长为60s时翼型壁面上的局部收集系数、对流换热系数和冻结系数的分布情况。由图3、图4和图5可以看出，经过每个结冰时间步长后，翼型原有的外形发生变化，壁面上的局部收集系数和对流换热系数随之变化，特别是驻点附近的变化最为明显。图6表示了从洁净翼型开始每隔60s的翼型表面冰形的变化过程。环境静温较高时，驻点区域冻结系数较小，结冰量小，未冻结的液态水在气流的吹拂下向下游溢流，最终形成槽状冰。驻点区域冰形变化复杂，导致局部收集系数和对流换热系数变化剧烈，这与图3和图4的结果也是相一致的。图7表示了本文预测的最终冰形与LEWICE冰风洞实验结果［16］和LEWICE软件计算结果［17］的对比情况。可以看出，本文结果与实验结果基本一致，上下壁面处结冰极限基本与实验结果相吻合，只是上壁面处冰角的厚度大于实验结果，但冰形的总体效果好于LEWICE软件计算结果。

3.2 环境温度为-28.4℃时的楔形冰计算

图8表示了环境静温为-28.4℃时经过360s生成的楔形冰，可以看出本文预测的冰形与实验结果［16］吻合的很好，只是在下壁面处结冰极限小于实验结果，这可能是结冰热力学模型中只考虑质量和能量守恒关系，而没有包含冻结过程中液态水在气动力作用下的运动规律。

图3 不同结冰时间局部收集系数分布图Fig.3 Local collection coefficient distribution of different icing time

图4 不同结冰时间壁面对流换热系数分布图Fig.4 Wall convective heat-transfer coefficient distribution of different icing time

图5 不同结冰时间冻结系数分布图Fig.5 Freeze fraction distribution of different icing time

3.3 环境温度为-13.4℃时的混合冰计算

图9表示了环境静温为-13.4℃时经过360s生成的典型的混合冰，可以看出本文结果在结冰极限位置与实验结果［16］基本一致，但是上壁面冰角处和下壁面溢流范围处的冰形均有明显差异，上壁面冰角的厚度小于实验结果。混合冰兼有槽状冰和楔形冰的特点，预测结果与实验结果有较明显差异，因此在结冰热力学模型方面需要进一步改进，对结冰过程的机理和细节需要深入研究。

4 结论

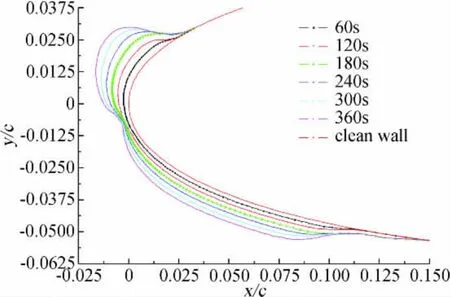
图6 不同结冰时间冰形图Fig.6 Ice shapes of different icing time

图7 环境温度为-6.1℃时的冰形比较Fig.7 Comparison of ice shapes at temperature-6.1℃

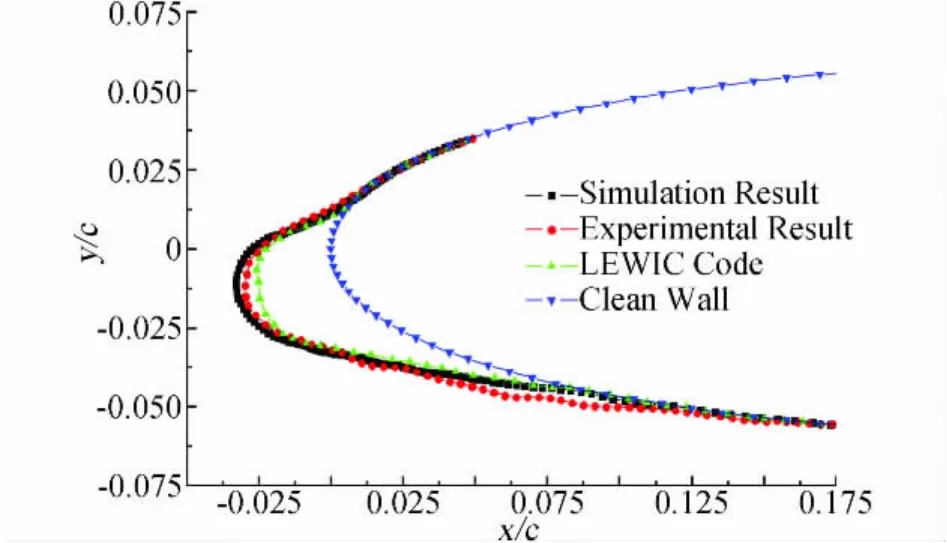
图8 环境温度为-28.4℃时的冰形比较Fig.8 Comparison of ice shapes at temperature-28.4℃

图9 环境温度为-13.4℃时的冰形比较Fig.9 Comparison of ice shapes at temperature-13.4℃

利用Fluent动网格模块对翼型表面的结冰过程进行了准定常模拟，在每个结冰时间步长内完成网格随着壁面边界的移动而更新、周围流场和水滴撞击特性重新计算、对流换热系数的重新计算结冰冰形计算及壁面边界的重构工作，最后计算了其它结冰条件相同而环境温度不同的三种典型冰形，将预测结果与冰风洞实验进行了比较，得到如下结论:

(1)利用Fluent动网格实现翼型结冰后的网格重构，可以避免对单个结冰时间结束后翼型边界发生变化后的流场计算区域重新生成网格，提高效率，具有实际应用价值。

(2)环境温度是影响冰形的重要参数。环境温度较高时，驻点区域冻结质量小，液态水向下游溢流，形成具有凹槽的槽状冰;环境温度很低时，液态水撞击到壁面立刻冻结，外形比较规则，形成楔形冰;环境温度较低时，冰形兼具槽状冰和楔形冰的特点，形成混合冰。

(3)利用Messinger结冰热力学模型结合Fluent动网格模块可以得到和实验结果比较吻合的计算结果，只是在局部区域有差异，一定程度上证明了本文所述方法的正确性和可行性，但对于该模型还需进一步改进和完善，特别是对结冰过程的机理需要深入研究。

［1］HAROLD E A，MARK G P，DAVID W S.Modern airfoil ice accretions［R］.AIAA 97-0174，1997.

［2］FORTIN G，PERRON J.CIRAAMIL ice accretion code improvement［R］.AIAA 2009-3968，2009

［3］张大林，陈维建.飞机机翼表面霜状冰结冰过程的数值模拟［J］.航空动力学报，2003，18(1):88～89.

［4］蒋胜矩，李凤蔚.基于 N-S方程的翼型结冰数值模拟［J］.西北工业大学学报，2004，22(5):559 ～560.

［5］易贤.飞机积冰的数值计算与积冰试验相似准则研究［D］.中国空气动力研究与发展中心研究生部，2007.

［6］常士楠，艾素霄，等.一种飞机机翼表面结冰过程仿真方法［J］.系统仿真学报，2008，20(10):2538 ～2539.

［7］裘爕纲，韩风华.飞机防冰系统［M］.北京:航空专业教材审编组，1985.

［8］JEROEN E D，HARRY W M.Numerical simulation of airfoil ice accretion and thermal anti-icing systems［R］.ICAS 2004-7.5.2，2004.

［9］KAYS W M，CRAWFORD M E.Convective heat and mass transfer［M］.Third Edition.Mc Graw-Hill，1993.

［10］JAIWON S，BRIAN B.Prediction of ice shapes and their effect on airfoil drag［J］.Journal of Aircraft，1994，31(2).

［11］DAVID N A，et al.Measurement and correlation of ice accretion roughness［R］.AIAA 98-0486，1998.

［12］VON DOENHOFF，HORTON E A.Low-speed experimental investigation of the effect of sandpaper type of roughness on boundary-layer transition［R］.NACA TN 3858，1956.

［13］MATHIEU F，SAEED F.PARASCHIVOIU I.Surface heat transfer study for ice accretion and anti-icing prediction in three dimension［R］.AIAA 2004-0063，2004.

［14］RUFF G A，BERKOWITZ B M.Users manual for the NASA Lewis ice accretion prediction code(LEWICE)［R］.NASA CR-18519，1990.

［15］MARK G P.LEWICE/E:an Euler based ice accretion code［R］.AIAA 92-0037，1992.

［16］SHIN J，BOND T H.Results of an icing test on a NACA0012 airfoil in the NASA Lewis icing research tunnel［R］.AIAA 92-0647，1992.

［17］MINGIONE G，BRANDI V，ESPOSITO B.Ice accretion prediction on multi-element airfoils［R］.AIAA 1997-0177，1997.