已知信道统计特性的时延—多普勒匹配滤波

贾艳云，赵航芳

(杭州应用声学研究所，浙江杭州310012)

0 引言

主动声纳系统性能直接与发射波形的特征(能量、形状等)相关联。Shannon、Nyquist等人早在上世纪就奠定了发射波形研究的基础。二次世界大战之后，对发射理论进一步做了发展［1］。但是这些都只考虑了距离(时延)分辨力或速度(多普勒)分辨力。为了能同时获得高的时延—多普勒分辨力，该文的主要工作是对发射波形和信道进行时延—多普勒表征［2－5］，在收—发等量齐观的前提下，进行时延—多普勒匹配滤波［6］，优化发射和处理波形，实现系统的期望响应最大。

1 模糊度函数及发射波形设计

时间特性和频率特性是信号的两大基本特性，时间特性用时延表征，频率特性用多普勒表征。而刻画信号时延—多普勒分辨特性的一个基本量是其模糊度函数，它描述了在无噪声条件下，由时延和多普勒频移引起的匹配滤波器失配时输出的变化情况，是时延和多普勒频移的两维自相关函数［2］。

窄带条件下波形f(t)和q(t)的互模糊度函数为:

式中，为时延，与目标的距离相关;v为窄带多普勒频移，与目标的径向速度相关。当波形f(t)和q(t)是同一个波形时，式1退化为自模糊度函数，其特性决定着匹配滤波波形的分辨特性和估计性能。模糊度函数的主瓣形状和峰值决定着参数估计能达到的精度和分辨力。研究各种声纳信号形式，实质上是研究信号的模糊度函数，信号的模糊度函数能够表征信号的基本特征。

主动声纳常用的PCW信号由于时间带宽积为1的限制，其高的多普勒分辨力是以牺牲脉宽为代价的。虽然LFM信号可以通过调节信号带宽和脉宽来分别获得高的时延和多普勒分辨力，但它是一个高耦合的信号，会带来因时延和多普勒间的耦合而造成的误差;HFM信号是一个多普勒宽容信号。上述几中信号均不满足时间带宽积一定条件下的高时延—多普勒分辨要求，需要进行波形设计。它指出在给定的设计带宽限制下，最大化模糊度函数主瓣的距离分辨力并最小化模糊度函数旁瓣的面积。同时也证明了具有理想图钉形状模糊度函数的波形可以通过在时频轴上接近均匀分布的波形获得［1］。

2 双扩展信道的时延—多普勒表征

海洋信道是一个左右对称上下不对称的有界非均匀环境，界面的影响使发射波形的传播有多条路经，每条路径的到达时间不同，导致了时延扩展，用以表征信道的传播特性;水层中散射体的随机运动和收发平台的相对运动导致了多普勒扩展，用以表征信道的动态特性。因而，海洋信道是一个双扩展信道，只是扩展而已。

通常用时变脉冲响应h(t，)描述随机时变线性系统［3，4］，它是一个随机量。若要了解系统的全局行为，可通过信号时频分析理论和相关处理来获得WSSUS下能够描述系统特性的二阶统计参量—散射函数［3－5］Ps(，v)。信道系统函数的傅里叶变换关系如图1所示，可以看出，对随机量h(t，)关于时间t作傅立叶变换，得到信道的扩展函数Ss(，v)，它仍是一个随机量，难以描述信道特性。WSSUS条件下，对扩展函数作自相关，得到信道的散射函数，它是一个功率谱密度函数，描述了发射波形经双扩展信道传播之后的平均时延和多普勒扩展量，可以完全表征信道的时延—多普勒扩展特性。发射波形f(t)经过双扩展信道传播之后，接收波形s(t)为发射波形的时延—多普勒频移之拷贝加权和，权系数为信道的扩展函数。

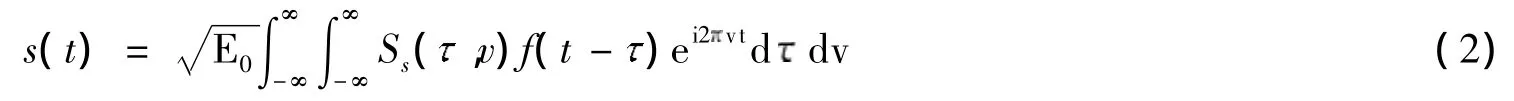
式中，E0为发射信号能量。

3 基于信道散射函数的时延—多普勒匹配滤波

主动声纳的待估量——距离和径向速度在实际中无法直接观测获得，需要转换到信号的某一参量域中作相应的处理，以获得高分辨力、低方差域辨识(估计)能力。距离域对应的是时延域，速度域对应的是多普勒域。本文研究的是单传感器在时延—多普勒域中的滤波问题:将信号和信道进行时延—多普勒表征，选择信道扩展函数为权系数，将互模糊度函数与信道散射函数进行相关。时延—多普勒匹配滤波器期望响应为:

式中，＊＊表示两维卷机。发射—处理波形的互模糊度函数与信道散射函数在时延—多普勒平面内的重叠面积决定了系统的响应如图2所示。

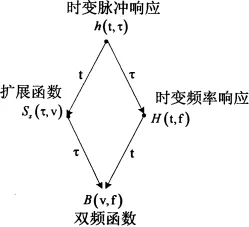
图1 信道系统函数傅立叶变换关系

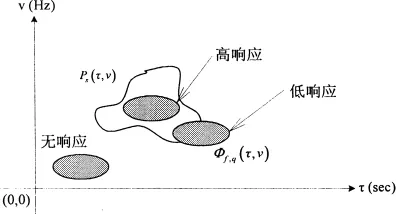
图2 信号和信道函数的重叠面积决定系统期望响应

定义窄带条件下双扩展信道中信号最佳检测的检验统计量为:

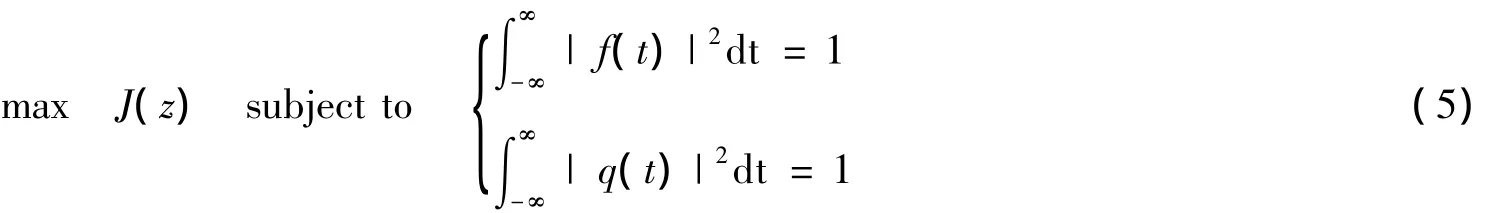
式4可以看出，时延—多普勒匹配滤波器的输出响应最大是一个泛函问题，当发射波形固定时，它通过互模糊度函数与处理波形发生联系;当处理波形固定时，它通过互模糊度函数与发射波形发生联系;当发射波形与处理波形都不固定时，它通过互模糊度函数与两者发生联系。泛函的最佳解不能解析表示，可以通过梯度投影算法［6］微观调整发射波形和处理波形，使其互模糊度函数与信道散射函数具有相似的形状来获得系统高的响应。

4 仿真分析

仿真条件:发射能量1 000J，带宽100Hz，中心频率2kHz，脉宽50ms的LFM-PCW组合随机加权复信号，采样频率为5kHz，信道的散射函数由一个两维高斯脉冲如图3(d)所示，最大时延扩展和时延采样频率分别为50ms和5kHz，最大多普勒扩展和多普勒采样间隔分别为75kHz和0.586kHz。初始的处理波形为发射波形的时延—多普勒频移加权求和。采用10%的升余弦窗对发射波形和处理波形加权。

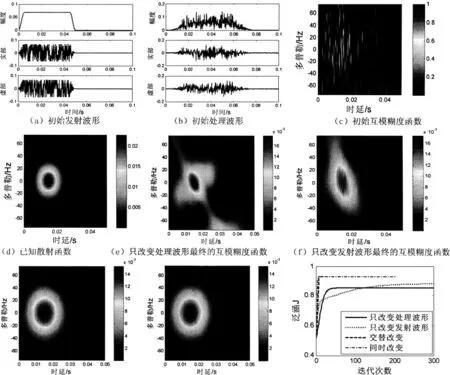
图3 白噪声背景下4种方法的波形优化结果

可以看出，利用梯度投影算法通过发—收联合优化发射波形和处理波形，可以将它们的互模糊度函数由初始的在时延—多普勒平面无规均匀分布调整到算法收敛时与信道散射函数具有相似的形状和分布，时延—多普勒匹配滤波器期望响应在算法迭代终止时达到最大。有限迭代次数限制下，滤波器期望响应大小顺序为:同时优化两种波形＞交替优化两种波形＞只优化单个波形［7］。算法收敛时，根据已知散射函数优化两种波形的互模糊度函数的体积分配结果好于只优化单一波形的体积分配结果;交替优化两种波形的滤波器期望输出可以媲美同时优化两种波形。

5 结束语

海洋信道是一个时延—多普勒双扩展信道，只有在充分了解和掌握信道特性的前提下，才能进行有效、可靠的信号处理。本文正是基于此，发射和接收同时考虑信道特性，系统期望响应达到最大。

［1］Woodward P M.Probability and Information Theory with Application to Radar［M］.London:Pergamon Press Publishers，1953:431－460.

［2］宫先仪.声场建模与模拟［R］.杭州:浙江大学信电系，2009:569－571.

［3］Ricker D W.Echo Signal Processing［M］.Bordrecht:Kluwer Academic Publishers，2003:319－405.

［4］Bello P A.Characterization of Randomly Time-Variant Linear Channels［J］.Commun Theory，1963，11(4):360－393.

［5］Kay S M，Doyle S B.Rapid Estimation of the Range-Doppler Scattering Function［J］.Signal Processing，2003，51(1):255－267.

［6］Drumheller D M，Ricker D W.Receiver-Transmitter Optimization for Detection in Doubly Spread Channels［J］.Journal of the Acoustical Society of America，1991，89(4):1 714－1 723.［7］贾艳云.发—收联合时延—多普勒匹配滤波［D］.北京:中国舰船研究院，2011:41－44.