低延迟误差IIR滤波器设计的迭代算法

杨吉祥，赖晓平，侯秀竹，罗家浩

(杭州电子科技大学信息与控制研究所，浙江杭州310018)

0 引言

数字滤波是数字信号处理中最重要的组成部分之一，与模拟滤波相比，它具有精度和稳定性高、灵活性强等优点。经过近几十年的研究，无限冲击响应(Infinite Impulse Response，IIR)数字滤波器的minimax设计问题得到了长足的发展。较早的一种minimax设计方法是线性规划［1］方法，这种方法需要较长的计算时间和很大的存储空间。另外一类方法是用迭代重加权技术把问题转化为一系列二次规划［2］问题或二阶锥规划［3］问题，再通过Matlab自带函数或其他方法近似求解。最近，文献4提出一种新的迭代机制，用序列约束最小二乘方法实现IIR数字滤波器的minimax设计。该方法将minimax问题化为一系列约束最小二乘问题，并用Levy－Sanathanan－Koerner(LSK)策略［5，6］将得到的非凸最小二乘子问题化为标准的凸优化问题，得到了比其它方法好的频率响应特性。本文对IIR数字滤波器相位误差进行约束，考虑具有给定相位误差上界的约束minimax设计问题，并应用相位误差上界函数的迭代更新技术［8］对相位误差约束进行自动修正，得到的群延迟误差在整个通带上近似均匀。设计实例表明该方法得到了较小的群延迟误差，有效抑制了带边群延迟大的效应。

1 设计问题的数学描述

一个IIR数字滤波器的系统函数表达式为:

式中，bm，m=0，1，…，M和μn，n=1，2，…，N分别表示H(z)的分子、分母的系数。当z=ejω替换时表示其频率响应，可用下式表示:

式中，μ=［μ1，μ2，L，μN］T，b=［b0，b1，L，bM］T均为实数，上标T表示矩阵转置，en(ω)=［1，e-jω，L，e-jMω］T，ed(ω)=［e-jω，e-j2ω，L，e-jNω］T，M和N分别为滤波器传递函数分子和分母的阶数。IIR数字滤波器的minimax设计就是在minimax优化准则下确定式2中的μ和b的值。本文是在对相位误差进行约束的同时对频率响应误差幅值的最大值进行极小，问题描述为如下的相位误差约束minimax问题:

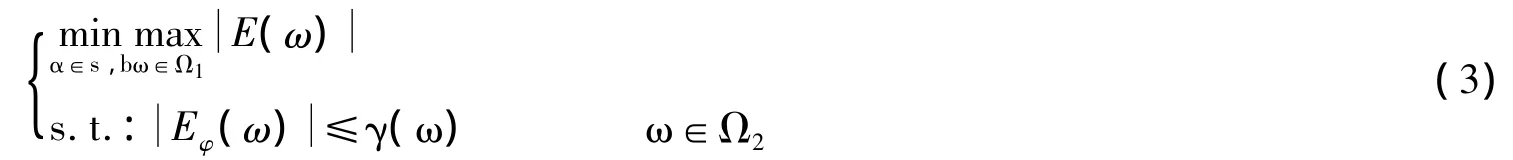
S是滤波器的稳定域。本文采用正实条件作为滤波器的稳定约束条件，可以表示为:

式中，r(r≤1)为极点半径参数，它表示将滤波器传递函数的极点约束在半径为r的圆内;ε是一个很小的接近于0的正数，Ω⊆［0，π]。Ω1为通带和阻带上的频率点集合，式3为相位误差约束，Ω2为施加相位约束的频率点集合，γ(ω)＞0为相位误差上界函数，式3中E(ω)为滤波器的实际频率响应与期望频率响应之差，即频率响应误差，式3中Eφ(ω)为滤波器的实际相位与期望相位之差，即相位误差。可以表示如下:

取相位误差导数的负数即得到群延迟误差，可用下面式子表示:

设x=［bT，μT］T，φ(ω)=［enT(ejω)，-D(ω)e(ejω)］，则频率响应误差可化为:

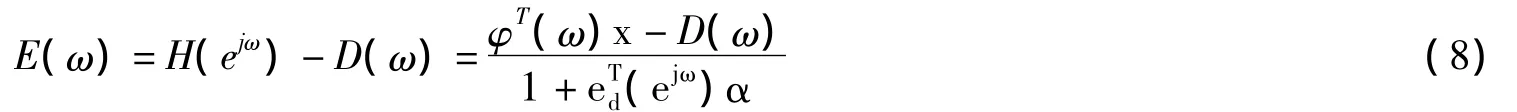
引进δ=max|E(ω)|，则相位约束minimax问题式3等价为下面问题:

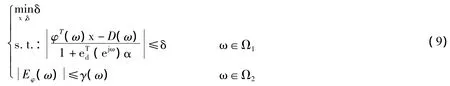
为了求解式9，采用文献4中的序列约束最小二乘方法，把问题转化为如下的一系列约束最小二乘问题:

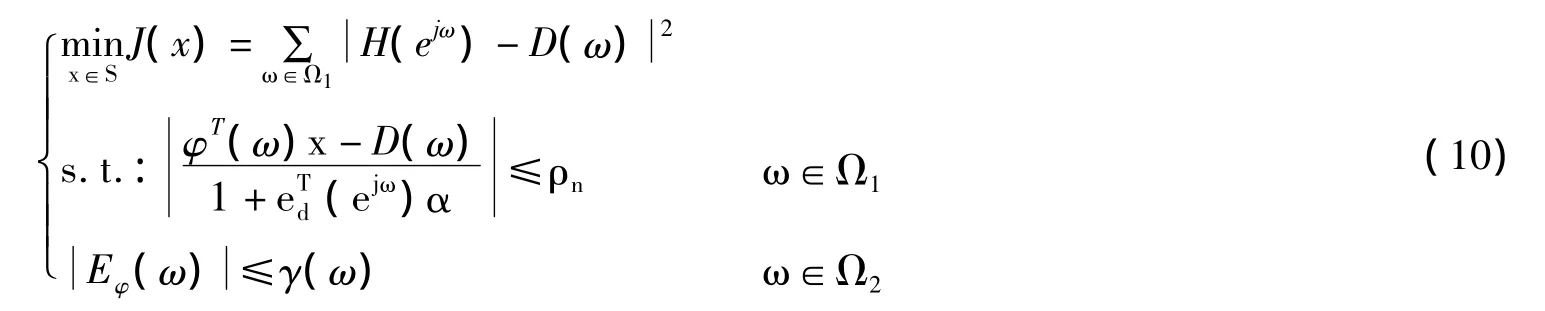
式中，{ρn:n=0，1，2，L}是一个频率响应误差幅值的上界序列。序列约束最小二乘方法中每个最小二乘子问题都是非凸优化问题。与文献4相同，本文采用LSK策略进行求解。

由文献7可知在较紧的上界约束下，相位误差响应在通带区域是等波纹的。但是在通带边缘处，由于振荡频率加快，导致群延迟误差在通带边界附近比较大。群延迟误差是相位误差的负导数，减小相位误差的振荡幅度可以减小群延迟误差，这样在趋向带边的区域对相位误差施加一个越来越紧的约束，就可以减小带边附近相位误差的振荡幅度，从而减小带边附近的群延迟误差。在文献8中，针对有限冲击响应滤波器的minimax设计中滤波器群延迟误差的减小问题提出了一种应用群延迟误差包络线自动更新相位误差上界函数的方法，有效减小了所设计有限冲击响应滤波器的群延迟误差。本文将该方法应用到IIR滤波器的相位误差约束minimax设计。在每一次的迭代步骤中，将上一次迭代得到的IIR数字滤波器群延迟的修正包络线的倒数与上次迭代的相位误差上界函数相乘，并将所得结果作为当前迭代的相位误差上界函数，对当前迭代中的相位误差进行约束。应用这种方法可以得到近似均匀的群延迟误差响应，从而达到减小群延迟误差的目的。

2 仿真实例

给出两个用自动更新相位误差上界函数的迭代算法来自动更新相位误差约束IIR数字滤波器的设计实例。例中缩减因子取θ=0.85，ε=0.000 001。加权函数在通带和阻带上都取1，过渡带为0，Ω取为{k/400|k=0，1，…，400}，Ω1为Ω中滤波器阻带和通带集合，Ω2为Ω中施加相位约束的频率点集合。数据表格中的MCE代表通带和阻带的最大复值误差，PMME代表通带的最大幅值误差，SMME代表阻带的最大幅值误差，MGE代表通带的群延迟误差，MPE代表通带相位误差，MPR表示极点半径。

例1设计一个低通IIR数字滤波器，阶数M=N=12，通带截止频率ωp=0.5，阻带截止频率ωs=0.6，群延迟=15.9。本例通带群延迟误差和相位误差曲线对比图如图1所示:

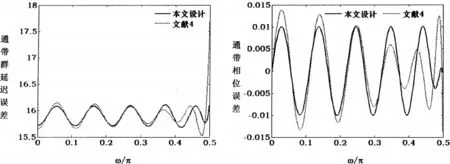
图1 通带群延迟误差和相位误差曲线图

例2设计一阶数M=10，N=6的低通IIR数字滤波器，通带截止频率ωp=0.3，阻带截止频率ωs=0.6，群延迟为6.25。本例通带群延迟误差和相位误差曲线对比图如图2所示:

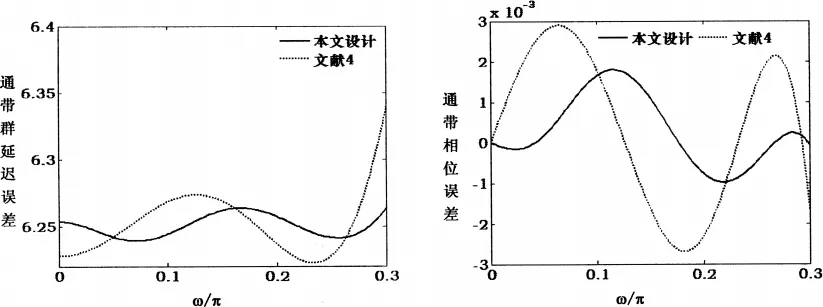
图2 通带群延迟误差和相位误差曲线图

例1与例2所得IIR数字滤波器相关数据如表1所示:

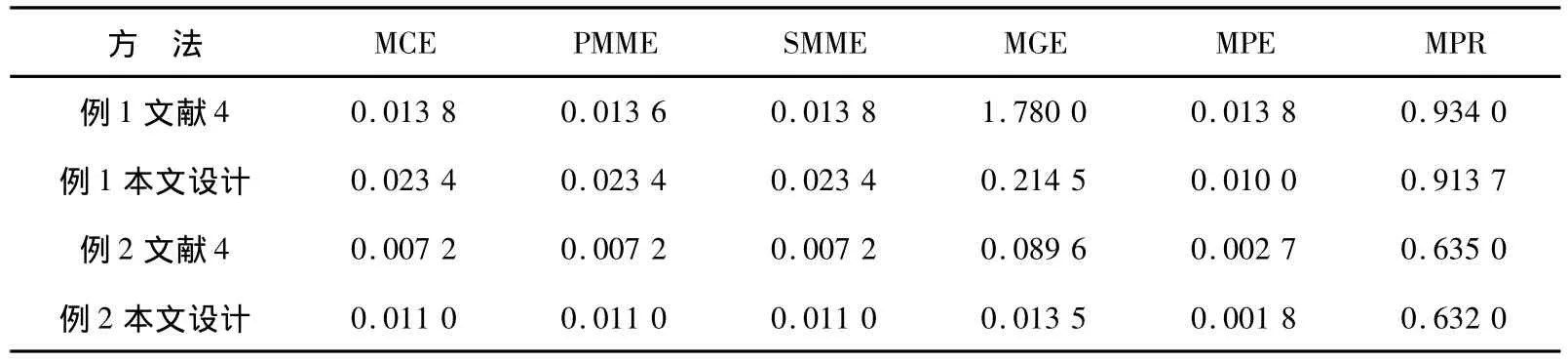
表1 该方法与文献4设计出的滤波器的频率响应特性比较

由图1、2和表1的数据可以看出本文中使用自动更新相位误差上界函数的迭代算法来自动更新相位误差约束得到的相位误差分布比较均匀，群延迟误差比较小，有效抑制了通带边缘群延迟误差大的效应，同时也得到了较小的相位误差，但幅值误差有所增大。

3 结束语

针对带相位误差约束IIR滤波器的minimax设计问题，本文应用了相位误差上界函数的迭代更新技术相位误差约束进行自动修正，并结合序列约束最小二乘方法把该问题化为一系列约束最小二乘子问题，通过求解这些子问题得到原问题的解。设计实例表明，该方法得到了较小的群延迟误差，有效抑制了带边群延迟大的效应。但此方法会使幅值误差有所增大。

［1］Chottera A T，Jullien G A.A Linear Programming Appro-ach to Recursive Digital Filter Design with Linear Phase［J］.IEEE Trans.on Circuits and Systems，1982，29(3):139－149.

［2］Tseng C C，Lee Su-Ling.Minimax Design of Stable IIR Filter with Prescribed Magnitude Phase Responses［J］.IEEE Trans.on Circrits and Systems I，2002，49(4):547－550.

［3］Lu W S，Hinamoto T.Optimal Design of IIR Digital Filters with Robust Stability Using Conic-quadratic Programming Updates［J］.IEEE Trans.on Signal Processing，2003，51(6):1 581－1 592.

［4］Lai X P.Minimax Design of IIR Digital Filters Using a Sequential Constrained Least-Squares Method［J］.IEEE Trans.on Signal Processing，2010，58(7):3 901－3 906.

［5］Sanathanan C K，Koerner J.Transfer Function Synthesis as A Ratio of Two Complex Polynomials［J］.on Automatic Control，1963，8(1):56－58.

［6］Levy.Complex Curve Fitting［J］.IRE Trans.on Automatic Control，1959，(4):37－43.

［7］Lai X P.Optimal Design of Nonlinear-phase FIR filters with Prescribed Phase Error［J］.IEEE Trans.on Signal Processing，2009，57(9):3 399－3 410.

［8］Lai X P，Lai C L，Zhao R J.An Iterative Approach to Near-Vniform Group-Delay Error Design of FIR Filters［J］.IEEE Signal Processing Leffers，2011，18(2):107－110.